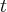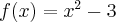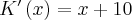Pochodna funkcji jednej zmiennej
| Strona: | WIKAMP Port |
| Przedmiot: | Pochodna funkcji jednej zmiennej |
| Książka: | Pochodna funkcji jednej zmiennej |
| Wydrukowane przez użytkownika: | Gość |
| Data: | czwartek, 15 stycznia 2026, 13:36 |
Spis treści
- Wstęp
- 1. Wprowadzenie
- 1.1 Pochodna funkcji w punkcie
- Teoria
- Przykłady
- Ćwiczenia interaktywne
- 1.2 Reguły różniczkowania
- Teoria
- Przykłady
- Ćwiczenia interaktywne, cz.1
- Ćwiczenia interaktywne, cz.2
- 1.3 Interpretacja geometryczna pochodnej w punkcie
- Teoria
- Przykłady
- Ćwiczenia interaktywne
- 1.4 Interpretacja fizyczna pochodnej w punkcie
- 1.5 Interpretacja ekonomiczna pochodnej w punkcie
- 1.6 Zadania
- 2. Twierdzenia o wartości średniej i wnioski z nich
- 3. Reguła de l'Hospitala
- 4. Monotoniczność funkcji, ekstrema lokalne i ekstrema globalne
- 5. Wypukłość, wklęsłość funkcji, punkty przegięcia
- 6. Badanie przebiegu zmienności funkcji
- 7. Pochodna w zastosowaniach praktycznych - przykłady
Wstęp
Kurs Pochodna funkcji jednej zmiennej przeznaczony jest dla studentów pierwszego roku uczelni wyższych, jak również dla zainteresowanych uczniów klas maturalnych. Znajdziemy w nim podstawowe definicje i twierdzenia związane z rachunkiem różniczkowym funkcji jednej zmiennej oraz różne przykłady zastosowania pochodnej.
Materiał zawarty w poszczególnych rozdziałach kursu podzielony jest na następujące części:
- Teoria – tu znajdziemy elementy teorii związanej z rachunkiem różniczkowym: definicje, twierdzenia oraz filmy,
- Przykłady – przykładowe zadania z rozwiązaniami ilustrowane interaktywnymi filmami,
- Ćwiczenia interaktywne – różnego typu interaktywne ćwiczenia do samodzielnego rozwiązania z możliwością sprawdzenia poprawności podanych odpowiedzi, na początku każdej strony z ćwiczeniami znajdują się również linki do wykorzystywanych definicji i twierdzeń,
- Zadania – zadania do samodzielnego rozwiązania z odpowiedziami i wskazówkami.
Wszystkie zamieszczone w kursie rysunki zostały wykonane za pomocą programu GeoGebra 6.0. W interaktywnych ćwiczeniach wykorzystano aplety GeoGebry oraz różnego typu zasoby H5P.
Kurs jako otwarty zasób edukacyjny został przygotowany w roku 2018 przez zespół wykładowców z Centrum Nauczania Matematyki i Fizyki Politechniki Łódzkiej w składzie: dr inż. Renata Długosz, dr Mariusz Doliński, dr inż. Gertruda Gwóźdź-Łukawska, dr inż. Izabela Jóźwik, dr inż. Elżbieta Kotlicka-Dwurznik, dr Joanna Kucner, dr Monika Lindner, dr inż. Agnieszka Niedziałkowska, dr Monika Potyrała, dr Joanna Rzepecka, dr inż. Małgorzata Terepeta, dr inż. Witold Walas.
1. Wprowadzenie
W tym rozdziale poznamy:
- definicję pochodnej
 funkcji w punkcie (właściwej i niewłaściwej)
funkcji w punkcie (właściwej i niewłaściwej) - definicję pochodnej jako funkcji
- definicję różniczki funkcji w punkcie
- reguły różniczkowania funkcji
- interpretację geometryczną, fizyczną i ekonomiczną pochodnej funkcji w punkcie.
Nauczymy się jak:
- badać istnienie pochodnej funkcji w punkcie korzystając z definicji
- obliczać pochodną funkcji korzystając ze wzorów na pochodną sumy, iloczynu, ilorazu funkcji, pochodną funkcji złożonej oraz pochodną funkcji odwrotnej
- wyznaczać przybliżoną wartość funkcji za pomocą różniczki
- wyznaczać równanie stycznej do wykresu funkcji w punkcie.
1.1 Pochodna funkcji w punkcie
W tym rozdziale dostępne są: Teoria, Przykłady, Ćwiczenia interaktywne.
Teoria
Załóżmy, że funkcja  jest określona na pewnym otoczeniu
jest określona na pewnym otoczeniu  punktu
punktu  . Niech
. Niech  będzie różnym od zera przyrostem zmiennej
będzie różnym od zera przyrostem zmiennej  takim, że
takim, że  należy do tego otoczenia. Niech
należy do tego otoczenia. Niech  będzie przyrostem wartości funkcji odpowiadającym przyrostowi
będzie przyrostem wartości funkcji odpowiadającym przyrostowi  . Ilorazem różnicowym funkcji
. Ilorazem różnicowym funkcji  w punkcie
w punkcie  dla przyrostu
dla przyrostu  nazywamy wyrażenie
nazywamy wyrażenie
Jeżeli istnieje i jest skończona granica
to nazywamy ją pochodną funkcji  w punkcie
w punkcie  i oznaczamy
i oznaczamy  lub
lub  . Zatem
. Zatem
(o ile granica ta istnieje i jest skończona).
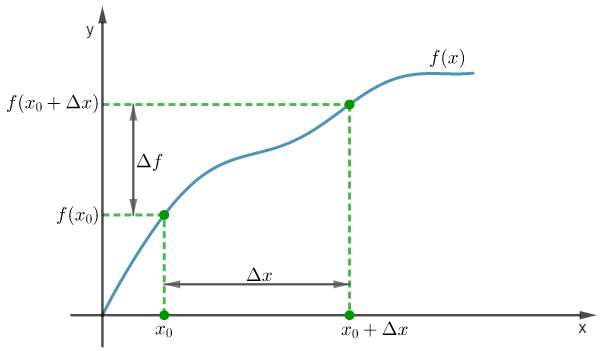
Funkcję jednej zmiennej, która ma pochodną w punkcie  nazywamy funkcją różniczkowalną w tym punkcie.
nazywamy funkcją różniczkowalną w tym punkcie.
Załóżmy, że funkcja  jest określona na pewnym prawostronnym otoczeniu
jest określona na pewnym prawostronnym otoczeniu  . Niech
. Niech  będzie różnym od zera przyrostem zmiennej
będzie różnym od zera przyrostem zmiennej  takim, że
takim, że  należy do tego otoczenia. Niech
należy do tego otoczenia. Niech  będzie przyrostem funkcji odpowiadającym przyrostowi
będzie przyrostem funkcji odpowiadającym przyrostowi  . Jeżeli istnieje i jest skończona granica
. Jeżeli istnieje i jest skończona granica
to nazywamy ją pochodną prawostronną funkcji  w punkcie
w punkcie  i oznaczamy
i oznaczamy 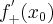 lub
lub  . Zatem
. Zatem
Załóżmy, że funkcja  jest określona na pewnym lewostronnym otoczeniu
jest określona na pewnym lewostronnym otoczeniu  . Niech
. Niech  będzie różnym od zera przyrostem zmiennej
będzie różnym od zera przyrostem zmiennej  takim, że
takim, że  należy do tego otoczenia. Niech
należy do tego otoczenia. Niech  będzie przyrostem funkcji odpowiadającym przyrostowi
będzie przyrostem funkcji odpowiadającym przyrostowi  . Jeżeli istnieje i jest skończona granica
. Jeżeli istnieje i jest skończona granica
to nazywamy ją pochodną lewostronną funkcji  w punkcie
w punkcie  i oznaczamy
i oznaczamy  . Zatem
. Zatem

Przykłady
Ćwiczenia interaktywne
Przypomnij sobie:
• definicję pochodnej funkcji w punkcie • warunek konieczny różniczkowalności funkcji w punkcie
Wskaż poprawne odpowiedzi.
Wskaż poprawne odpowiedzi.
Udziel odpowiedzi na pytania.
1.2 Reguły różniczkowania
W tym rozdziale dostępne są: Teoria, Przykłady, Ćwiczenia interaktywne.
Teoria
Przykłady
Korzystając ze wzorów bezpośrednich i praw działań na pochodnych obliczymy pochodne funkcji:
Korzystając ze wzorów bezpośrednich i praw działań na pochodnych oraz twierdzenia o pochodnej funkcji złożonej obliczymy pochodne funkcji:
Ćwiczenia interaktywne, cz.1
Przypomnij sobie:
• wzory na pochodną sumy, iloczynu i ilorazu funkcji • wzory na pochodne podstawowych funkcji elementarnych
Uzupełnij:
Uzupełnij:
Uzupełnij:
Uzupełnij:
Ćwiczenia interaktywne, cz.2
Przypomnij sobie:
• wzory na pochodną sumy, iloczynu i ilorazu funkcji • wzory na pochodne podstawowych funkcji elementarnych
Oblicz pierwszą i drugą pochodną funkcji  .
.
Uzupełnij. Edycja tekstów w GeoGebrze
1.3 Interpretacja geometryczna pochodnej w punkcie
W tym rozdziale dostępne są: Teoria, Przykłady, Ćwiczenia interaktywne.
Teoria

Iloraz różnicowy 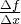 równy jest tangensowi kąta
równy jest tangensowi kąta  nachylenia prostej (siecznej) przechodzącej przez punkty
nachylenia prostej (siecznej) przechodzącej przez punkty  i
i  :
:
Jeżeli granica  istnieje i jest skończona, to jej wartość równa jest tangensowi kąta
istnieje i jest skończona, to jej wartość równa jest tangensowi kąta  nachylenia stycznej do wykresu funkcji
nachylenia stycznej do wykresu funkcji  poprowadzonej w punkcie
poprowadzonej w punkcie  , zatem
, zatem

Pochodna  jest równa współczynnikowi kierunkowemu stycznej do wykresu funkcji
jest równa współczynnikowi kierunkowemu stycznej do wykresu funkcji  poprowadzonej w punkcie
poprowadzonej w punkcie  .
.
Przykłady
Ćwiczenia interaktywne
Przypomnij sobie:
• definicję stycznej do wykresu funkcji w punkcie • postać równania stycznej
Wyznacz równanie stycznej do wykresu funkcji  w punkcie
w punkcie  .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz równanie stycznej do wykresu funkcji  w punkcie
w punkcie 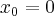 .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz równanie stycznej do wykresu funkcji  w punkcie
w punkcie  .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz równanie stycznej do wykresu funkcji  w punkcie
w punkcie  .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
1.4 Interpretacja fizyczna pochodnej w punkcie
Dokładniejszą charakterystykę szybkości zmian funkcji otrzymamy wtedy, gdy w powyższym ilorazie przejdziemy do granicy. Konieczna jest jednak znajomość analitycznego wzoru rozważanej funkcji.
Potrzebę wprowadzenia pochodnej objaśnimy na przykładzie fizycznych wielkości:
Rozpatrzmy ruch po linii prostej, aby nie trzeba się było posługiwać wektorami.
Wyobraźmy sobie punkt materialny  poruszający się ze zmienną prędkością po osi liczbowej
poruszający się ze zmienną prędkością po osi liczbowej  w taki sposób, że jego pozycja w chwili
w taki sposób, że jego pozycja w chwili 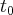 określona jest jako funkcja czasu i wynosi
określona jest jako funkcja czasu i wynosi 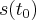 . W chwili
. W chwili 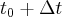 współrzędna (pozycja) tego punktu jest równa
współrzędna (pozycja) tego punktu jest równa 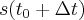 . Przesunięcie w czasie
. Przesunięcie w czasie 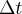 jest równe
jest równe 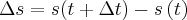 . Zatem prędkość średnia jest równa
. Zatem prędkość średnia jest równa

zaś prędkość chwilowa w chwili 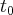 jest równa
jest równa
W czasie 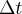 punkt materialny
punkt materialny 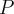 przyspieszy od chwili
przyspieszy od chwili 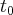 do chwili
do chwili 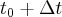 średnio o
średnio o
Granicę właściwą tego ilorazu różnicowego, gdy 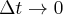 nazywamy przyspieszeniem punktu
nazywamy przyspieszeniem punktu 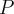 w chwili
w chwili 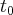
Prąd elektryczny to uporządkowany ruch ładunków elektrycznych wzdłuż przewodnika. Niech 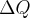 oznacza ładunek przepływający przez ustalony przekrój przewodnika w czasie
oznacza ładunek przepływający przez ustalony przekrój przewodnika w czasie 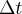 . Wówczas wielkość
. Wówczas wielkość 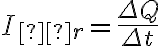 nazywa się średnim natężeniem prądu. Chwilowym natężeniem prądu jest wielkość
nazywa się średnim natężeniem prądu. Chwilowym natężeniem prądu jest wielkość
Załóżmy, że mamy pręt o długości  taki, że masa części tego pręta liczona od początku do punktu
taki, że masa części tego pręta liczona od początku do punktu ![x_0\in[0,L] x_0\in[0,L]](https://port.edu.p.lodz.pl/filter/tex/pix.php/8404e782da29421699c17ef81bc7ddb3.png) dana jest funkcją
dana jest funkcją 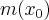 . Wtedy masa zawarta w przedziale
. Wtedy masa zawarta w przedziale ![[x_0,x_0+\Delta x] [x_0,x_0+\Delta x]](https://port.edu.p.lodz.pl/filter/tex/pix.php/bcb0a767217de0ecff1971b6e8b2bb02.png) wynosi:
wynosi:
Średnia gęstość masy na tym przedziale jest równa:
1.5 Interpretacja ekonomiczna pochodnej w punkcie
Wielkość przeciętna określa, w jakim stopniu funkcja  jest czuła na przyrost zmiennej
jest czuła na przyrost zmiennej  . Jednakże ocena reakcji funkcji na podstawie wzoru (1) daje pogląd jedynie na przeciętną prędkość zmiany wartości tej funkcji w przedziale
. Jednakże ocena reakcji funkcji na podstawie wzoru (1) daje pogląd jedynie na przeciętną prędkość zmiany wartości tej funkcji w przedziale ![[x_0,x_0+\Delta x] [x_0,x_0+\Delta x]](https://port.edu.p.lodz.pl/filter/tex/pix.php/bcb0a767217de0ecff1971b6e8b2bb02.png) . Zmiany te nie muszą zachodzić tak równomiernie, jak wskazuje wartość średnia. Dokładniejszą charakterystykę szybkości zmian funkcji otrzymamy wtedy, gdy w ilorazie (1) przejdziemy do granicy. Konieczna jest jednak znajomość analitycznego wzoru rozważanej funkcji.
. Zmiany te nie muszą zachodzić tak równomiernie, jak wskazuje wartość średnia. Dokładniejszą charakterystykę szybkości zmian funkcji otrzymamy wtedy, gdy w ilorazie (1) przejdziemy do granicy. Konieczna jest jednak znajomość analitycznego wzoru rozważanej funkcji.
Zauważmy, że dla funkcji jednej zmiennej  , dla małych przyrostów
, dla małych przyrostów  mamy:
mamy:
Niech 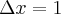 , czyli argument zwiększa się o jednostkę w stosunku do poziomu wyjściowego. Wtedy powyższa zależność ma postać:
, czyli argument zwiększa się o jednostkę w stosunku do poziomu wyjściowego. Wtedy powyższa zależność ma postać:
czyli zwiększenie argumentu o jednostkę powoduje wzrost funkcji o  . Zatem wielkość krańcowa funkcji jest w przybliżeniu równa przyrostowi funkcji przy wzroście argumentu funkcji o jednostkę. Wielkość krańcowa jest miarą szybkości zmian wartości funkcji w punkcie
. Zatem wielkość krańcowa funkcji jest w przybliżeniu równa przyrostowi funkcji przy wzroście argumentu funkcji o jednostkę. Wielkość krańcowa jest miarą szybkości zmian wartości funkcji w punkcie  .
.
Przykłady
1. Funkcja kosztu
Koszt wytworzenia dowolnej wielkości produkcji zależy od wielkości nakładów poszczególnych czynników produkcji oraz ich cen. Jest on więc funkcją kilku zmiennych. Jeżeli jednak nasze rozważania ograniczymy do krótkiego okresu, a więc czasu, w którym przynajmniej jeden czynnik produkcji jest stały i koszt możemy przedstawić jako funkcję jednej zmiennej: wielkości produkcji.
Koszty całkowite są sumą kosztów stałych i kosztów zmiennych.
Niech  będzie funkcją kosztu całkowitego zależną od wielkości produkcji
będzie funkcją kosztu całkowitego zależną od wielkości produkcji  , gdzie
, gdzie  . Wtedy funkcję
. Wtedy funkcję
nazywamy funkcją kosztów przeciętnych, a jej wartość 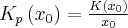 kosztem przeciętnym (jednostkowym) wytworzenia jednostki produktu przy poziomie produkcji
kosztem przeciętnym (jednostkowym) wytworzenia jednostki produktu przy poziomie produkcji  .
.
Przy podejmowaniu decyzji dotyczących wielkości produkcji (i jej wpływu na koszty) bardzo ważną wskazówką jest kształtowanie się kosztów jednostkowych przy różnych rozmiarach produkcji. W tego typu analizach przydatne jest wykorzystanie kosztów krańcowych.
Koszt krańcowy to koszt wytworzenia dodatkowej jednostki produktu (przy założeniu, że produkcja zmienia się skokowo), czyli przyrost kosztów spowodowany zwiększeniem produkcji o jednostkę. Tak więc koszty krańcowe informują o tym, jak wzrosną koszty całkowite przy wzroście produkcji o jedną jednostkę  Często jednak zakładamy ciągłą, a nie skokową zmianę wielkości produkcji.
Często jednak zakładamy ciągłą, a nie skokową zmianę wielkości produkcji.
Przy założeniu, że funkcja  jest różniczkowalna oraz
jest różniczkowalna oraz  ,
,  ,
,  , gdzie
, gdzie  jest dodatnim przyrostem argumentu funkcji (przyrostem produkcji), można zbudować iloraz różnicowy (przyrost przeciętny) tej funkcji:
jest dodatnim przyrostem argumentu funkcji (przyrostem produkcji), można zbudować iloraz różnicowy (przyrost przeciętny) tej funkcji:
Wyraża on przeciętny koszt wytworzenia dodatkowych jednostek produktu  poczynając od poziomu
poczynając od poziomu  . Granicą tego ilorazu jest pochodna funkcji
. Granicą tego ilorazu jest pochodna funkcji  w punkcie
w punkcie 
Stąd
Natomiast funkcja 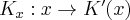 jest funkcją kosztu krańcowego.
jest funkcją kosztu krańcowego.
2. Funkcja produkcji
Funkcja produkcji określa relacje między wielkością produkcji a liczbą zaangażowanych czynników produkcji. Funkcja produkcji określa, jaką maksymalną wielkość produkcji może osiągnąć przedsiębiorstwo w wyniku użycia posiadanych zasobów, przy danej technice wytwarzania.
Funkcja produkcji
gdzie:  ‒ całkowita wielkość produkcji;
‒ całkowita wielkość produkcji;  ‒ ilość użytych jednostek kapitału;
‒ ilość użytych jednostek kapitału;  ‒ ilość użytych jednostek pracy.
‒ ilość użytych jednostek pracy.
Jak widać (po uproszczeniu) produkcja zależy od zaangażowanych w nią kapitału i pracy. Krótki okres (SR) to taki czas (stan), w którym ilość jednego lub więcej czynników produkcji jest stała (przynajmniej jeden czynnik produkcji jest stały, pozostałe mogą być zmienne).
- Produkt całkowity T(total) P(product) to łączna wielkość produkcji przedsiębiorstwa wytwarzana przy zatrudnianiu kolejnych jednostek zmiennego czynnika wytwórczego.

-
Produkt przeciętny A(average)P(product) to średnia wielkość produkcji całkowitej
 przypadająca na jednostkę zmiennego czynnika wytwórczego
przypadająca na jednostkę zmiennego czynnika wytwórczego  lub
lub  .
. - Produkt marginalny (krańcowy) M(marginal) P(product) to przyrost produkcji (
 ) wynikający z zatrudnienia dodatkowego pracownika (
) wynikający z zatrudnienia dodatkowego pracownika ( ) lub dodatkowej jednostki zmiennego czynnika produkcji (
) lub dodatkowej jednostki zmiennego czynnika produkcji ( ).
).
Prawo malejących dochodów głosi, że jeżeli następuje wzrost nakładów jednego czynnika produkcji (przy założeniu stałości pozostałych czynników), to począwszy od pewnego poziomu, przyrosty produkcji zaczynają maleć. Formuła liczenia:
3. Funkcja konsumpcji
Dochody gospodarstw domowych mają być przeznaczone na wydatki konsumpcyjne lub na oszczędności  . Przy danym poziomie dochodów im większe wydatki konsumpcyjne, tym mniejsze oszczędności i odwrotnie, im większe oszczędności, tym mniejsze wydatki konsumpcyjne. Wynika z tego, że decyzje gospodarstw domowych w sprawie wydatków konsumpcyjnych są zarazem decyzjami w sprawie oszczędzania. Funkcja konsumpcji pokazuje poziom zamierzonych łącznych wydatków konsumpcyjnych przy różnych poziomach dochodu. Zależność (liniową) między wydatkami konsumpcyjnymi a dochodem charakteryzuje skłonność do konsumpcji.
. Przy danym poziomie dochodów im większe wydatki konsumpcyjne, tym mniejsze oszczędności i odwrotnie, im większe oszczędności, tym mniejsze wydatki konsumpcyjne. Wynika z tego, że decyzje gospodarstw domowych w sprawie wydatków konsumpcyjnych są zarazem decyzjami w sprawie oszczędzania. Funkcja konsumpcji pokazuje poziom zamierzonych łącznych wydatków konsumpcyjnych przy różnych poziomach dochodu. Zależność (liniową) między wydatkami konsumpcyjnymi a dochodem charakteryzuje skłonność do konsumpcji.
- Przeciętna skłonność do konsumpcji to stosunek wydatków konsumpcyjnych do dochodu. Wielkość ta informuje, jaka części dochodu przeznaczona jest na konsumpcję:
 .
. - Krańcowa skłonność do konsumpcji to stosunek przyrostu wydatków konsumpcyjnych do przyrostu dochodu. Wielkość ta informuje jaka część przyrostu dochodu przeznaczona jest na wydatki konsumpcyjne:
W polityce gospodarczej znajomość krańcowej skłonności do konsumpcji ma duże znaczenie. Pozwala bowiem odpowiedzieć, z dużą dozą prawdopodobieństwa, na co ludzie przeznaczą dodatkowe dochody i w jakiej proporcji wydadzą je na dobra konsumpcyjne, a ile zaoszczędzą.
4. Funkcja użyteczności
Funkcja użyteczności to funkcja, której wartościami są wartości użyteczności (satysfakcji, komfortu psychicznego). Można mówić o użyteczności różnych zjawisk (koszyków towarów). Użyteczność pieniądza (bogactwa) jest np. funkcją, która wartości pieniężnej przyporządkowuje użyteczność dla otrzymującego tę wartość. Funkcja użyteczności jest pojęciem psychologicznym, co oznacza, że każdy ma swoją funkcję użyteczności. Jednak pewne ogólne własności są wspólne. Mianowicie, ponieważ każdy woli posiadać więcej niż mniej, więc funkcja użyteczności jest rosnąca. Ponadto krańcowa użyteczność jest malejąca, tzn. każdy dodatkowy procent wzrostu bogactwa powoduje coraz mniejszy przyrost użyteczności. Przykładowo, ktoś kto nic nie ma, podejmie wysiłek w celu zarobienia  zł., bo ta kwota zapewni mu np. posiłek. Dla osoby bogatej ta kwota będzie prawie bez znaczenia.
zł., bo ta kwota zapewni mu np. posiłek. Dla osoby bogatej ta kwota będzie prawie bez znaczenia.
Funkcja użyteczności 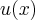 jest funkcją spełniającą warunki:
jest funkcją spełniającą warunki:
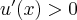 ‒ postulat niedosytu oznacza, że wzrost ilości towaru w koszyku zwiększa użyteczności koszyka,
‒ postulat niedosytu oznacza, że wzrost ilości towaru w koszyku zwiększa użyteczności koszyka, ‒ krańcowa użyteczność każdego towaru maleje, w miarę jak wzrasta jego spożycie.
‒ krańcowa użyteczność każdego towaru maleje, w miarę jak wzrasta jego spożycie.
 .
.2. Twierdzenia o wartości średniej i wnioski z nich
W tym rozdziale poznamy:
- twierdzenie
 Rolle'a i twierdzenie
Rolle'a i twierdzenie Lagrange'a
Lagrange'a - wnioski z twierdzenia Lagrange'a dotyczące monotoniczności funkcji
- twierdzenie
 Taylora.
Taylora.
Nauczymy się jak
- wykorzystać rachunek różniczkowy w dowodzeniu tożsamości (nie tylko trygonometrycznych)
- wyznaczać wielomiany Taylora i wielomiany Maclaurina dla wybranych funkcji.
2.1 Twierdzenie Rolle'a i twierdzenie Lagrange'a
W tym rozdziale dostępne są: Teoria, Przykłady, Ćwiczenia interaktywne.
Teoria
Iloraz  równy jest tangensowi kąta
równy jest tangensowi kąta  nachylenia prostej (siecznej) przechodzącej przez punkty
nachylenia prostej (siecznej) przechodzącej przez punkty 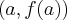 i
i 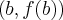 .
.
Z twierdzenie Lagrange'a wnioskujemy, że na wykresie funkcji  znajduje się przynajmniej jeden taki punkt (o odciętej
znajduje się przynajmniej jeden taki punkt (o odciętej 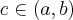 ), w którym styczna do wykresu funkcji
), w którym styczna do wykresu funkcji  jest równoległa do prostej przechodzącej przez punkty
jest równoległa do prostej przechodzącej przez punkty 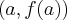 i
i 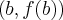 .
.

Wnioski z twierdzenia Lagrange'a
Implikacje odwrotne do podanych we wniosku 3 i wniosku 4 nie zachodzą. W szczególności nie jest prawdą, że jeżeli  jest funkcją rosnącą na przedziale
jest funkcją rosnącą na przedziale  , to
, to  dla każdego
dla każdego  . Przykładem jest funkcja
. Przykładem jest funkcja  , która jest ściśle rosnąca, ale jej pochodna
, która jest ściśle rosnąca, ale jej pochodna  zeruje się w punkcie
zeruje się w punkcie  .
.
Wnioski 3 i 4 nie zachodzą w przypadku, gdy przedział  zastąpimy sumą przedziałów.
zastąpimy sumą przedziałów.
Przykłady
Rozważmy funkcję 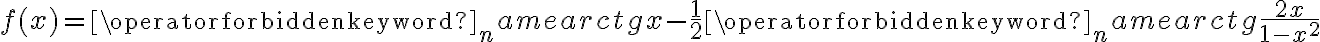 . Zauważmy, że jej dziedziną jest zbiór
. Zauważmy, że jej dziedziną jest zbiór 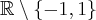 , zatem funkcja
, zatem funkcja  jest poprawnie określona na przedziale
jest poprawnie określona na przedziale 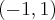 . Obliczmy pochodną funkcji
. Obliczmy pochodną funkcji  :
:
Obliczamy pierwszą i drugą pochodną funkcji  :
:
Zatem 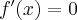 na każdym przedziale zawartym w dziedzinie tej funkcji, zatem w szczególności na
na każdym przedziale zawartym w dziedzinie tej funkcji, zatem w szczególności na 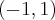 . Na mocy wniosku 1 otrzymujemy, że
. Na mocy wniosku 1 otrzymujemy, że  jest stała na tym przedziale, czyli istnieje stała
jest stała na tym przedziale, czyli istnieje stała  taka, że dla każdego
taka, że dla każdego 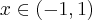 zachodzi równość
zachodzi równość 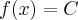 .
.
Obliczymy wartość funkcji  dla argumentu
dla argumentu  .
.
Ćwiczenia interaktywne
2.2 Twierdzenie Taylora
W tym rozdziale dostępne są: Teoria, Przykłady, Ćwiczenia interaktywne.
Teoria
Powyższy wzór nazywany jest wzorem Taylora, zaś wyrażenie 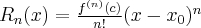 resztą Taylora w postaci Lagrange'a. Wielomian postaci
resztą Taylora w postaci Lagrange'a. Wielomian postaci
nazywamy wielomianem Taylora stopnia  w punkcie
w punkcie  .
.
Jeżeli  , to wzór Taylora ma postać
, to wzór Taylora ma postać
i nazywany jest wzorem Maclaurina (punkt  leży pomiędzy
leży pomiędzy  i
i  ). Pomijając w powyższym wzorze resztę Taylora
). Pomijając w powyższym wzorze resztę Taylora 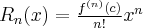 , otrzymujemy przybliżenie (aproksymację) funkcji
, otrzymujemy przybliżenie (aproksymację) funkcji  za pomocą wielomianu Maclaurina:
za pomocą wielomianu Maclaurina:
przy czym błąd bezwzględny tego przybliżenia wynosi 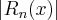 . Jeżeli wszystkie pochodne funkcji
. Jeżeli wszystkie pochodne funkcji  są wspólnie ograniczone, to
są wspólnie ograniczone, to 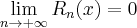 . Wówczas możemy obliczyć wartość funkcji
. Wówczas możemy obliczyć wartość funkcji  z dowolną dokładnością.
z dowolną dokładnością.
Przybliżenie wybranych funkcji za pomocą wzoru Maclaurina:
Przykłady
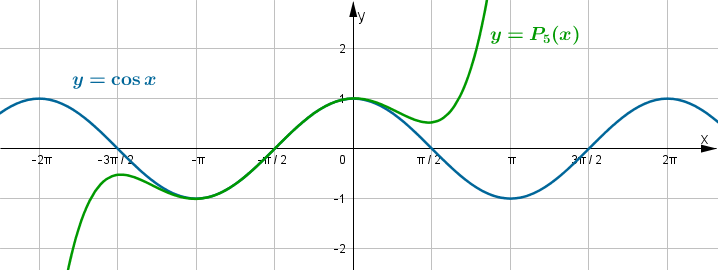
Pochodne funkcji 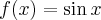 , począwszy od rzędu pierwszego do piątego, są odpowiednio równe
, począwszy od rzędu pierwszego do piątego, są odpowiednio równe
- Wyznaczamy wartość funkcji
 i jej pochodnych dla
i jej pochodnych dla 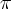 :
:
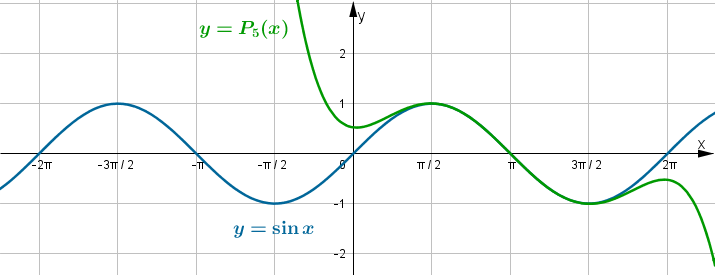
Zatem wielomianem Taylora stopnia piątego w punkcie
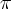 dla funkcji
dla funkcji 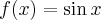 jest
jestPoniżej przedstawiamy wykres funkcji
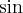 i jej wielomianu Taylora
i jej wielomianu Taylora 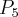 w punkcie
w punkcie 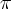 .
.
- Wartości
 i jej pochodnych dla argumentów
i jej pochodnych dla argumentów 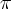 i
i 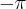 są sobie równe. Stąd wielomianem Taylora stopnia piątego w punkcie
są sobie równe. Stąd wielomianem Taylora stopnia piątego w punkcie 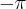 dla funkcji
dla funkcji 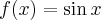 jest
jest
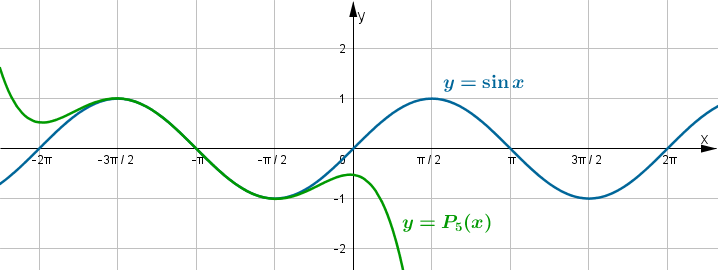
Poniżej znajduje się wykres funkcji
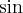 i jej wielomianu Taylora
i jej wielomianu Taylora 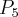 w punkcie
w punkcie  .
.
Pochodne funkcji 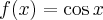 , począwszy od rzędu pierwszego do piątego, są odpowiednio równe
, począwszy od rzędu pierwszego do piątego, są odpowiednio równe
- Wyznaczamy wartość funkcji
 i jej pochodnych dla
i jej pochodnych dla 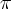 :
:
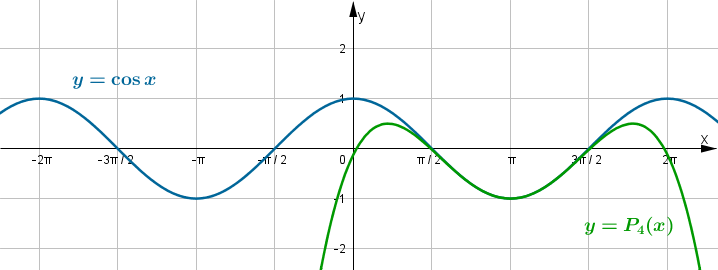
Zatem wielomianem Taylora stopnia czwartego w punkcie
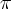 dla funkcji
dla funkcji  jest
jestPoniżej przedstawiamy wykres funkcji
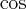 i jej wielomianu Taylora
i jej wielomianu Taylora 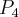 w punkcie
w punkcie 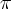 .
.
- Wyznaczamy wartość funkcji
 i jej pochodnych dla
i jej pochodnych dla 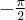 :
:
Wielomianem Taylora stopnia piątego w punkcie
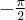 dla funkcji
dla funkcji 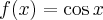 jest więc
jest więcPoniżej przedstawiamy wykres funkcji
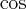 i jej wielomianu Taylora
i jej wielomianu Taylora 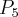 w punkcie
w punkcie 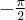 .
.
Ćwiczenia interaktywne
Przypomnij sobie:
• twierdzenie Taylora • przybliżenia wybranych funkcji za pomocą wielomianów Maclaurina
Przyporządkuj funkcji jej przybliżenie za pomocą wielomianu Maclaurina.
Wyznacz wielomian Maclaurina  stopnia
stopnia  dla funkcji
dla funkcji 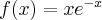 .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Wyznacz wielomian Taylora  stopnia
stopnia  dla funkcji
dla funkcji  w punkcie
w punkcie  .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Wyznacz wielomian Taylora  stopnia
stopnia  dla funkcji
dla funkcji  w punkcie
w punkcie  .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Przykłady
Obliczymy granice funkcji stosując regułę de l'Hospitala:
- Zaczynamy od określenia symbolu granicy, aby zdecydować, czy można zastosować regułę de l'Hospitala. Następnie badamy, czy istnieje granica ilorazu pochodnych: Na mocy reguły de l'Hospitala otrzymujemy odpowiedź
- Zwykle stosując regułę de l'Hospitala stosujemy uproszczony zapis przedstawiony poniżej.
- Określamy symbol badanej granicy: Symbol granicy jest oznaczony, a zatem w tym przypadku nie można wykorzystać reguły de l'Hospitala. Aby obliczyć granicę należy zastosować odpowiednie twierdzenia arytmetyki granic funkcji: Na koniec zauważmy, że w tym przypadku a zatem granica ilorazu pochodnych różni się od badanej granicy. Przykład ten pokazuje, iż stosowanie reguły de l'Hospitala bez sprawdzenia założeń tego twierdzenia może prowadzić do błędnej odpowiedzi.
Obliczymy granice funkcji stosując regułę de l'Hospitala:
- Obliczymy podaną granicę funkcji stosując regułę de l'Hospitala:
- W przypadku tej granicy regułę de l'Hospitala zastosujemy dwukrotnie:
- Obliczymy podaną granicę funkcji stosując regułę de l'Hospitala i wykorzystując fakt, że
 .
.
- Podobnie jak w poprzednich przykładach zaczynamy od określenia symbolu badanej granicy
przy czym
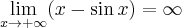 na mocy twierdzenia o dwóch funkcjach. W tym przypadku nie możemy wykorzystać reguły de l'Hospitala, gdyż
zaś taka granica nie istnieje. Nie oznacza to jednak, że nie istnieje badana granica – trzeba tylko policzyć ją innym sposobem. Ponieważ
oraz
na mocy twierdzenia o dwóch funkcjach. W tym przypadku nie możemy wykorzystać reguły de l'Hospitala, gdyż
zaś taka granica nie istnieje. Nie oznacza to jednak, że nie istnieje badana granica – trzeba tylko policzyć ją innym sposobem. Ponieważ
oraz  , więc na mocy twierdzenia o trzech funkcjach
, więc na mocy twierdzenia o trzech funkcjach 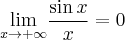 . Stąd
. Stąd
- W tym przypadku a zatem stosowanie reguły de l'Hospitala nie jest efektywne. Granicę funkcji możemy jednak obliczyć w inny sposób:
- Zaczynamy od określenia symbolu badanej granicy funkcji:
W tym przypadku, aby zastosować regułę de l'Hospitala, wyrażenie
 zapiszemy w postaci ilorazu
zapiszemy w postaci ilorazu  . Dwukrotnie stosując regułę de l'Hospitala otrzymujemy:
. Dwukrotnie stosując regułę de l'Hospitala otrzymujemy:
- Podobnie jak poprzednim przykładzie określimy najpierw symbol badanej granicy funkcji:
Następnie przekształcimy funkcję, której granicę obliczamy, w taki sposób by można było zastosować regułę de l'Hospitala. A zatem
- Ustalimy najpierw symbol badanej granicy funkcji:
Przekształcimy funkcję stosując tożsamość:
 . A zatem
. A zatem
Korzystając z wyniku otrzymanego w podpunkcie (b) mamy
![\left[\infty-\infty\right] \left[\infty-\infty\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/0a4382dc250cc70672eb67f35df398fa.png) , które po odpowiednich przekształceniach sprowadzimy do symbolu
, które po odpowiednich przekształceniach sprowadzimy do symbolu ![\left[ \frac{\infty}{\infty} \right] \left[ \frac{\infty}{\infty} \right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/de5999aa6f0b4ca90cab98e7c03f31a2.png) albo
albo ![\left[ \frac{0}{0} \right] \left[ \frac{0}{0} \right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/8e3f348a630785530b38a36fe9e9c071.png) .
.- Określamy symbol granicy i przekształcamy funkcję w następujący sposób:
Dalej pomocniczo obliczymy granicę
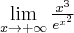 dwukrotnie stosując regułę de l'Hospitala:
Ostatecznie otrzymujemy
dwukrotnie stosując regułę de l'Hospitala:
Ostatecznie otrzymujemy
- Określamy symbol granicy: W tym przypadku, aby można było wykorzystać regułę de l'Hospitala, wystarczy sprowadzić ułamki do wspólnego mianownika. A zatem
- Stosujemy regułę de l'Hospitala po wykonaniu odpowiednich przekształceń:
Ćwiczenia interaktywne
Przypomnij sobie:
W przypadku których z poniższych symboli granic funkcji możemy bezpośrednio zastosować regułę de l'Hospitala?
Określ, czy podany symbol granicy jest oznaczony czy nieoznaczony, oraz czy możemy w takiej sytuacji bezpośrednio zastosować regułę de l'Hospitala:
Przeciągnij poprawne odpowiedzi w odpowiednie pola.
Oblicz podane granice.
Uzupełnij puste pola. Edycja tekstów w GeoGebrze
Oblicz podane granice. Czy i ile razy stosowałeś regułę de l'Hospitala?
Przeciągnij i upuść poprawne odpowiedzi.
Oblicz podane granice. Czy i ile razy stosowałeś regułę de l'Hospitala?
Przeciągnij i upuść poprawne odpowiedzi.
Oblicz podaną granicę.
Uzupełnij puste pola. Edycja tekstów w GeoGebrze
Oblicz podane granice stosując regułę de l'Hospitala po wykonaniu odpowiednich przekształceń.
Uzupełnij puste pola. Edycja tekstów w GeoGebrze
Zadania
4.1 Badanie monotoniczności funkcji
W tym rozdziale dostępne są: Teoria, Przykłady, Ćwiczenia interaktywne.
Teoria
- Jeżeli
 dla każdego
dla każdego  , to funkcja
, to funkcja  jest stała na przedziale
jest stała na przedziale  .
. - Jeżeli
 dla każdego
dla każdego  , to funkcja
, to funkcja  jest rosnąca na przedziale
jest rosnąca na przedziale  .
. - Jeżeli
 dla każdego
dla każdego  , to funkcja
, to funkcja  jest malejąca na przedziale
jest malejąca na przedziale  .
. - Jeżeli
 dla każdego
dla każdego  , to funkcja
, to funkcja  jest niemalejąca na przedziale
jest niemalejąca na przedziale  .
. - Jeżeli
 dla każdego
dla każdego  , to funkcja
, to funkcja  jest nierosnąca na przedziale
jest nierosnąca na przedziale  .
.
Zwróćmy uwagę, że w powyższych twierdzeniach dotyczących związku znaku pochodnej funkcji z jej monotonicznością zakładamy, że funkcja  jest określona na przedziale otwartym. Twierdzenia pozostają prawdziwe również w przypadku przedziałów domkniętych, jednostronnie domkniętych, czy też nieograniczonych. Natomiast nie można ich stosować np. dla funkcji określonej na zbiorze będącym sumą rozłącznych przedziałów.
jest określona na przedziale otwartym. Twierdzenia pozostają prawdziwe również w przypadku przedziałów domkniętych, jednostronnie domkniętych, czy też nieograniczonych. Natomiast nie można ich stosować np. dla funkcji określonej na zbiorze będącym sumą rozłącznych przedziałów.
Rozważmy funkcję  ,
,  . Pochodna tej funkcji jest równa
. Pochodna tej funkcji jest równa  dla
dla  . Zatem
. Zatem  dla każdego
dla każdego  . Funkcja jest więc malejąca na przedziale
. Funkcja jest więc malejąca na przedziale  i funkcja jest malejąca na przedziale
i funkcja jest malejąca na przedziale  . Natomiast nie jest prawdą, że funkcja
. Natomiast nie jest prawdą, że funkcja  jest malejąca na zbiorze
jest malejąca na zbiorze  .
.
Przykłady
Aby wyznaczyć dziedzinę funkcji  należy rozwiązać nierówność
należy rozwiązać nierówność 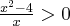 . Ponieważ
. Ponieważ
zatem 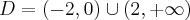 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
Zauważamy, że pochodna funkcji jest dodatnia w całej dziedzinie. Nie oznacza to jednak, że funkcja jest rosnąca w całej dziedzinie, gdyż dziedzina nie jest przedziałem a sumą przedziałów. A zatem stwierdzamy, że funkcja  jest rosnąca na przedziale
jest rosnąca na przedziale 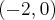 i na przedziale
i na przedziale  .
.
Dziedziną funkcji jest zbiór 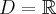 . Obliczamy pochodną funkcji:
. Obliczamy pochodną funkcji:
Aby wyznaczyć przedziały monotoniczności funkcji  badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Ponieważ
badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Ponieważ 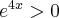 dla każdego
dla każdego  więc
więc
Zatem badana funkcja jest rosnąca na przedziale 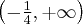 oraz malejąca na przedziale
oraz malejąca na przedziale 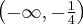 .
.
Z uwagi 2 wynika, że funkcja  jest również monotoniczna na przedziałach domkniętych, tzn. rosnąca na przedziale
jest również monotoniczna na przedziałach domkniętych, tzn. rosnąca na przedziale 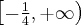 oraz malejąca na przedziale
oraz malejąca na przedziale ![\left(-\infty, -\frac14\right] \left(-\infty, -\frac14\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/05f7716a9abeb6d2ce9ac2ef90409b4c.png) – są to maksymalne przedziały monotoniczności funkcji
– są to maksymalne przedziały monotoniczności funkcji  .
.
Ćwiczenia interaktywne
Przypomnij sobie:
• warunki wystarczające monotoniczności funkcji
Wyznacz przedziały monotoniczności funkcji określonej wzorem 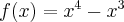 .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz przedziały monotoniczności funkcji określonej wzorem 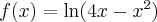 .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
4.2 Ekstrema lokalne funkcji
W tym rozdziale dostępne są: Teoria, Przykłady, Ćwiczenia interaktywne.
Teoria
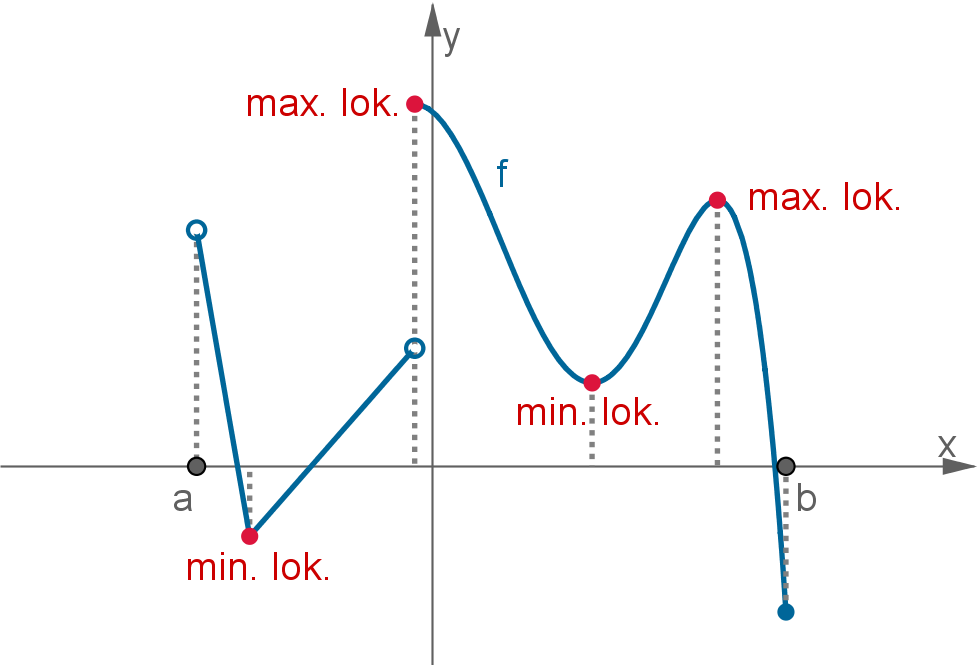
Mówimy, że funkcja  ma w punkcie
ma w punkcie  maksimum lokalne, jeżeli istnieje zawarte w dziedzinie funkcji
maksimum lokalne, jeżeli istnieje zawarte w dziedzinie funkcji  otoczenie
otoczenie  punktu
punktu  takie, że dla wszystkich
takie, że dla wszystkich 
Mówimy, że funkcja  ma w punkcie
ma w punkcie  minimum lokalne, jeżeli istnieje zawarte w dziedzinie funkcji
minimum lokalne, jeżeli istnieje zawarte w dziedzinie funkcji  otoczenie
otoczenie  punktu
punktu  takie, że dla wszystkich
takie, że dla wszystkich 
Jeżeli dla każdego  zachodzi nierówność
zachodzi nierówność 
 , to mówimy o maksimum (minimum) lokalnym właściwym.
, to mówimy o maksimum (minimum) lokalnym właściwym.
Jeżeli funkcja  jest różniczkowalna w punkcie
jest różniczkowalna w punkcie  i ma w tym punkcie ekstremum lokalne, to
i ma w tym punkcie ekstremum lokalne, to 
Funkcja  może mieć ekstremum lokalne jedynie w punkcie
może mieć ekstremum lokalne jedynie w punkcie  , takim że
, takim że  (gdy jest różniczkowalna w
(gdy jest różniczkowalna w  ) lub w punkcie
) lub w punkcie  , w którym funkcja
, w którym funkcja  nie ma pochodnej.
nie ma pochodnej.
Punkty, w których pochodna funkcji zeruje się nazywamy punktami stacjonarnymi tej funkcji.
Jeżeli funkcja  jest ciągła na pewnym otoczeniu
jest ciągła na pewnym otoczeniu  i różniczkowalna na sąsiedztwie
i różniczkowalna na sąsiedztwie  punktu
punktu  oraz
oraz
lub
to funkcja  ma w punkcie
ma w punkcie  ekstremum
ekstremum  lokalne właściwe. Jest to maksimum lokalne w przypadku 1 oraz minimum lokalne, gdy zachodzi warunek 2.
lokalne właściwe. Jest to maksimum lokalne w przypadku 1 oraz minimum lokalne, gdy zachodzi warunek 2.
Jeżeli funkcja  jest dwukrotnie różniczkowalna na pewnym otoczeniu punktu
jest dwukrotnie różniczkowalna na pewnym otoczeniu punktu  oraz
oraz
to funkcja  ma w punkcie
ma w punkcie  ekstremum
ekstremum  lokalne właściwe, przy czym jest to maksimum lokalne, jeżeli
lokalne właściwe, przy czym jest to maksimum lokalne, jeżeli  oraz minimum lokalne, gdy
oraz minimum lokalne, gdy  .
.
Przykłady
Funkcja  jest wielomianem, zatem dziedziną funkcji jest zbiór
jest wielomianem, zatem dziedziną funkcji jest zbiór 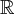 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
Ponieważ 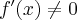 dla
dla  , więc
, więc  nie ma punktów stacjonarnych i w konsekwencji nie ma też ekstremów lokalnych (stosujemy wniosek z warunku koniecznego istnienia ekstremum lokalnego).
nie ma punktów stacjonarnych i w konsekwencji nie ma też ekstremów lokalnych (stosujemy wniosek z warunku koniecznego istnienia ekstremum lokalnego).
Obliczamy pochodną funkcji:
Wyznaczamy punkty stacjonarne funkcji  rozwiązując równanie:
rozwiązując równanie: 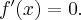
Wyznaczymy ekstrema lokalne funkcji określonej wzorem 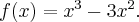
Zadanie rozpoczynamy od określenia dziedziny funkcji (w tym przypadku 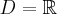 ) i zbadania, czy funkcja posiada punkty stacjonarne. Obliczamy pochodną funkcji
) i zbadania, czy funkcja posiada punkty stacjonarne. Obliczamy pochodną funkcji  :
:
Rozwiązujemy odpowiednie równanie:
Oba rozwiązania należą do dziedziny funkcji, a zatem  ma dwa punkty stacjonarne. Dalej rozstrzygamy o istnieniu ekstremów lokalnych w tych punktach stosując jedną z dwóch metod podanych poniżej.
ma dwa punkty stacjonarne. Dalej rozstrzygamy o istnieniu ekstremów lokalnych w tych punktach stosując jedną z dwóch metod podanych poniżej.
1 sposób (wykorzystujemy I warunek wystarczający istnienia ekstremum lokalnego)
Badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne:
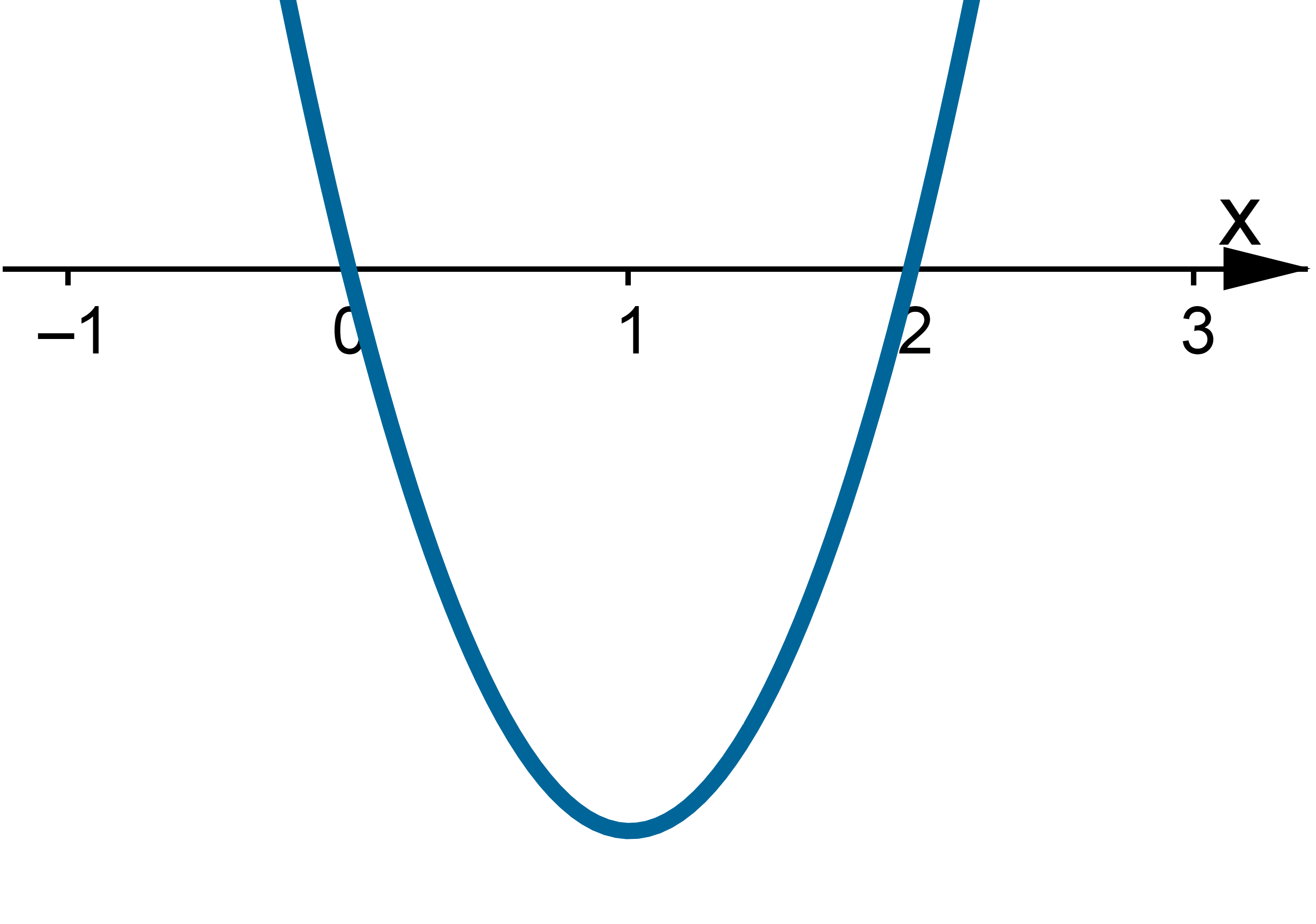 |
Stąd wynika, że 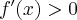 dla
dla 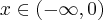 (a zatem także dla pewnego lewostronnego sąsiedztwa
(a zatem także dla pewnego lewostronnego sąsiedztwa  ) oraz
) oraz  dla
dla 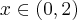 (przedział ten można potraktować jako prawostronne sąsiedztwo
(przedział ten można potraktować jako prawostronne sąsiedztwo  ). To oznacza, że
). To oznacza, że  ma w punkcie
ma w punkcie  maksimum lokalne
maksimum lokalne Pododnie
Pododnie  dla
dla 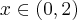 oraz
oraz 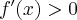 dla
dla 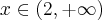 , czyli
, czyli  ma w punkcie
ma w punkcie  minimum lokalne.
minimum lokalne.
Metodę tę stosujemy najczęściej wtedy, gdy jednocześnie mamy wyznaczyć przedziały monotoniczności funkcji  .
.
2 sposób (wykorzystujemy II warunek wystarczający istnienia ekstremum lokalnego)
Obliczamy drugą pochodną funkcji  :
:
Ponieważ 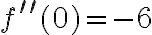 , a zatem
, a zatem  ma w punkcie
ma w punkcie  maksimum lokalne. Ponadto
maksimum lokalne. Ponadto 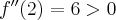 , co oznacza, że
, co oznacza, że  ma w punkcie
ma w punkcie  minimum lokalne.
minimum lokalne.
Ostatecznie stwierdzamy, że funkcja  posiada dwa ekstrema lokalne: maksimum lokalne w punkcie
posiada dwa ekstrema lokalne: maksimum lokalne w punkcie  o wartości
o wartości  oraz minimum lokalne w punkcie
oraz minimum lokalne w punkcie  o wartości
o wartości 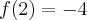 .
.
Wyznaczymy ekstrema lokalne funkcji określonej wzorem 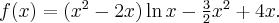
Funkcja  jest przykładem funkcji, dla której szukając ekstremów lokalnych wygodniej jest stosować II warunek wystarczający.
jest przykładem funkcji, dla której szukając ekstremów lokalnych wygodniej jest stosować II warunek wystarczający.
Dziedziną funkcji  jest zbiór
jest zbiór 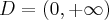 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  i zapisujemy ją w postaci iloczynowej:
i zapisujemy ją w postaci iloczynowej:
Wyznaczamy punkty stacjonarne funkcji  :
:
Dalej obliczamy drugą pochodną funkcji  :
:
Ponieważ
zatem  ma w punkcie
ma w punkcie 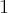 maksimum lokalne równe
maksimum lokalne równe 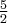 . Z kolei
. Z kolei
a zatem  ma w punkcie
ma w punkcie  minimum lokalne równe
minimum lokalne równe 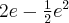 .
.
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji określonej wzorem 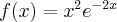 .
.
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji określonej wzorem 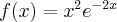 .
.
Na początek zauważmy, że 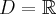 . Obliczamy pochodną funkcji i zapisujemy ją w postaci iloczynowej:
. Obliczamy pochodną funkcji i zapisujemy ją w postaci iloczynowej:
Wyznaczamy punkty stacjonarne funkcji  :
:
To oznacza, że funkcja  ma dwa punkty stacjonarne. Aby sprawdzić, czy
ma dwa punkty stacjonarne. Aby sprawdzić, czy  ma w nich ekstrema lokalne, zastosujemy I warunek wystarczający istnienia ekstremum lokalnego. W tym celu badamy, gdzie pochodna funkcji
ma w nich ekstrema lokalne, zastosujemy I warunek wystarczający istnienia ekstremum lokalnego. W tym celu badamy, gdzie pochodna funkcji  przyjmuje wartości dodatnie, a gdzie ujemne:
przyjmuje wartości dodatnie, a gdzie ujemne:
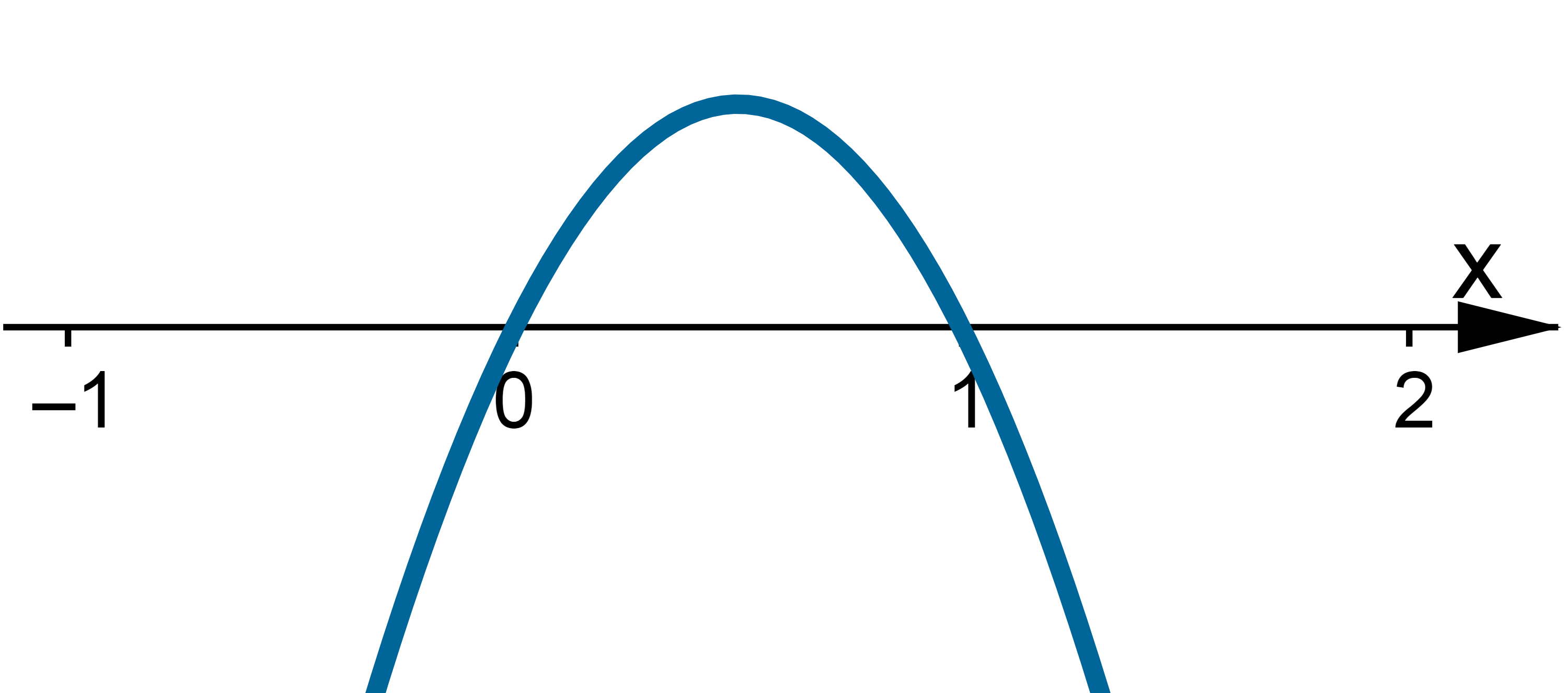
Stąd wynika, że istnieją sąsiedztwa 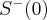 i
i 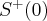 takie, że
takie, że 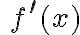 dla
dla 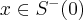 oraz
oraz 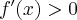 dla
dla 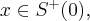 czyli
czyli  ma w
ma w  minimum lokalne. Podobnie uzasadniamy, że w
minimum lokalne. Podobnie uzasadniamy, że w 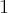 istnieje maksimum lokalne.
istnieje maksimum lokalne.
Uzyskane wyniki i odpowiedź (uwzględniając również przedziały monotoniczności badanej funkcji) najczęściej zapisujemy w postaci tabeli.

Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji określonej wzorem 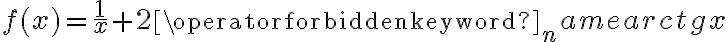 .
.
Na początek zauważmy, że 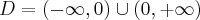 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
Wyznaczamy punkty stacjonarne funkcji  :
:
Następnie badamy, gdzie pochodna funkcji  przyjmuje wartości dodatnie, a gdzie ujemne. Ponieważ
przyjmuje wartości dodatnie, a gdzie ujemne. Ponieważ 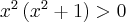 dla każdego
dla każdego 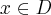 oraz
oraz
więc
Analogicznie
Uzyskane wyniki zapisujemy w tabeli:
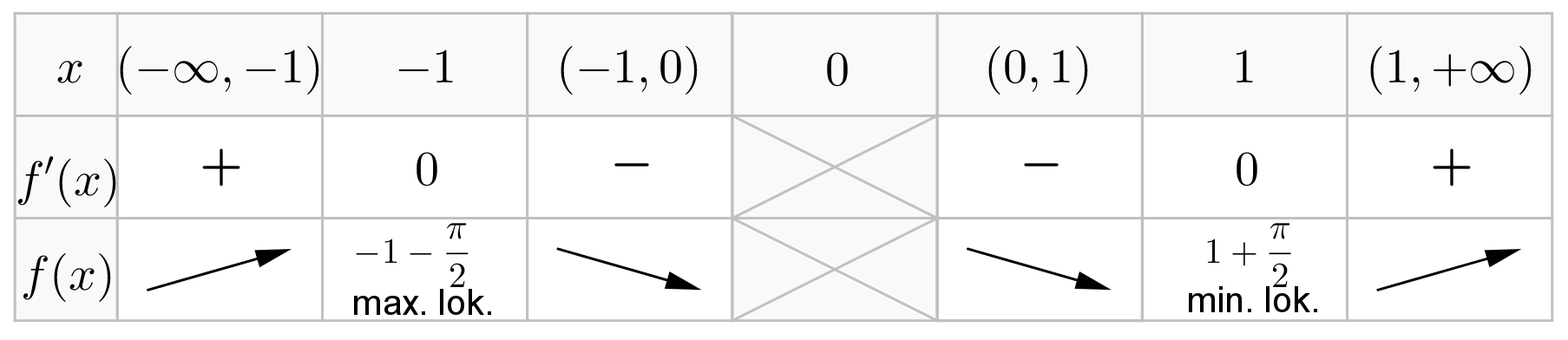
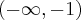 i
i 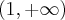 oraz malejąca na przedziałach
oraz malejąca na przedziałach 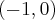 i
i 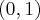 . Ponadto posiada dwa ekstrema lokalne: w punkcie
. Ponadto posiada dwa ekstrema lokalne: w punkcie  maksimum lokalne równe
maksimum lokalne równe 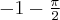 oraz w punkcie
oraz w punkcie 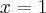 minimum lokalne równe
minimum lokalne równe 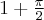 .
.Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji określonej wzorem 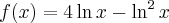 .
.
Na początek zauważmy, że 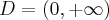 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
 :
:
Jeśli 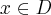 , to mianownik pierwszej pochodnej jest dodatni, a zatem
, to mianownik pierwszej pochodnej jest dodatni, a zatem
Analogicznie
Uzyskane wyniki zapisujemy w tabeli:
A zatem badana funkcja jest rosnąca na przedziae 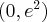 , malejąca na przedziale
, malejąca na przedziale 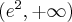 oraz posiada maksimum lokalne w
oraz posiada maksimum lokalne w 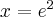 równe
równe  .
.
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji określonej wzorem 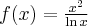 , a następnie naszkicujemy wykres funkcji
, a następnie naszkicujemy wykres funkcji  wiedząc dodatkowo, że
wiedząc dodatkowo, że 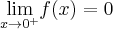 ,
, 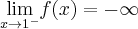 ,
, 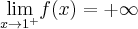 oraz
oraz 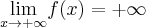 .
.
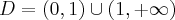 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
Wyznaczamy punkty stacjonarne funkcji  :
:
Analogicznie
Uzyskane wyniki zapisujemy w tabeli:
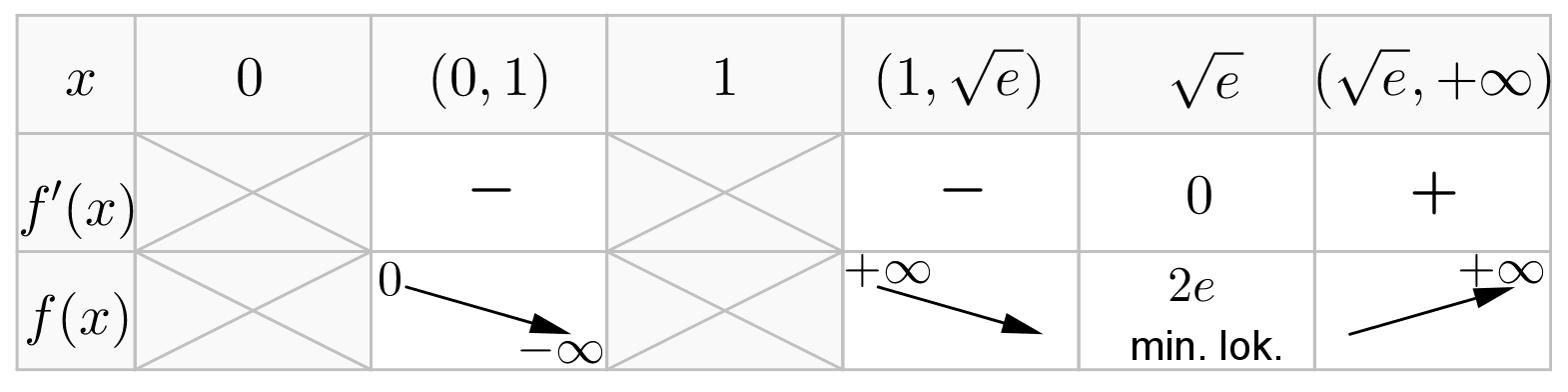
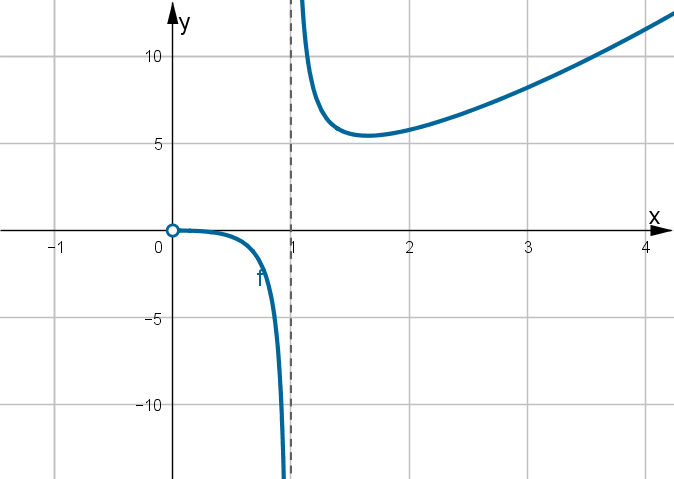
Badana funkcja jest zatem rosnąca na przedziale  , malejąca na przedziałach
, malejąca na przedziałach  i
i  oraz posiada w
oraz posiada w 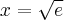 minimum lokalne równe
minimum lokalne równe 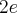 . Dodatkowo z informacji podanych w treści zadania wnioskujemy, że prosta o równaniu
. Dodatkowo z informacji podanych w treści zadania wnioskujemy, że prosta o równaniu 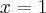 jest asymptotą pionową wykresu funkcji
jest asymptotą pionową wykresu funkcji  . Na tej podstawie szkicujemy wykres funkcji
. Na tej podstawie szkicujemy wykres funkcji  :
:
Ćwiczenia interaktywne, cz.1
Przypomnij sobie:
• definicje ekstremów lokalnych • warunek konieczny istnienia ekstremum lokalnego • I warunek wystarczający istnienia ekstremum lokalnego • II warunek wystarczający istnienia ekstremum lokalnego
Przyporządkuj podane funkcje do odpowiedniej grupy.
Przeciągnij poprawne odpowiedzi w odpowiednie pola.
Czy funkcja  posiada ekstrema lokalne we wskazanych punktach? Uzasadnij odpowiedź.
posiada ekstrema lokalne we wskazanych punktach? Uzasadnij odpowiedź.
Uzupełnij.
Czy funkcja  posiada ekstrema lokalne we wskazanych punktach? Uzasadnij odpowiedź.
posiada ekstrema lokalne we wskazanych punktach? Uzasadnij odpowiedź.
Uzupełnij.
Ćwiczenia interaktywne, cz.2
Przypomnij sobie:
• definicje ekstremów lokalnych • warunek konieczny istnienia ekstremum lokalnego • I warunek wystarczający istnienia ekstremum lokalnego • II warunek wystarczający istnienia ekstremum lokalnego
Wyznacz ekstrema lokalne funkcji  określonej wzorem
określonej wzorem 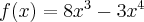 .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz ekstrema lokalne funkcji  określonej wzorem
określonej wzorem 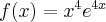 .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz ekstrema lokalne funkcji  określonej wzorem
określonej wzorem 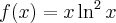 .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz przedziały monotoniczności i ekstrema lokalne funkcji  określonej wzorem
określonej wzorem 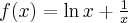 .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
4.3 Ekstrema globalne funkcji
W tym rozdziale dostępne są: Teoria, Przykłady, Ćwiczenia interaktywne.
Teoria
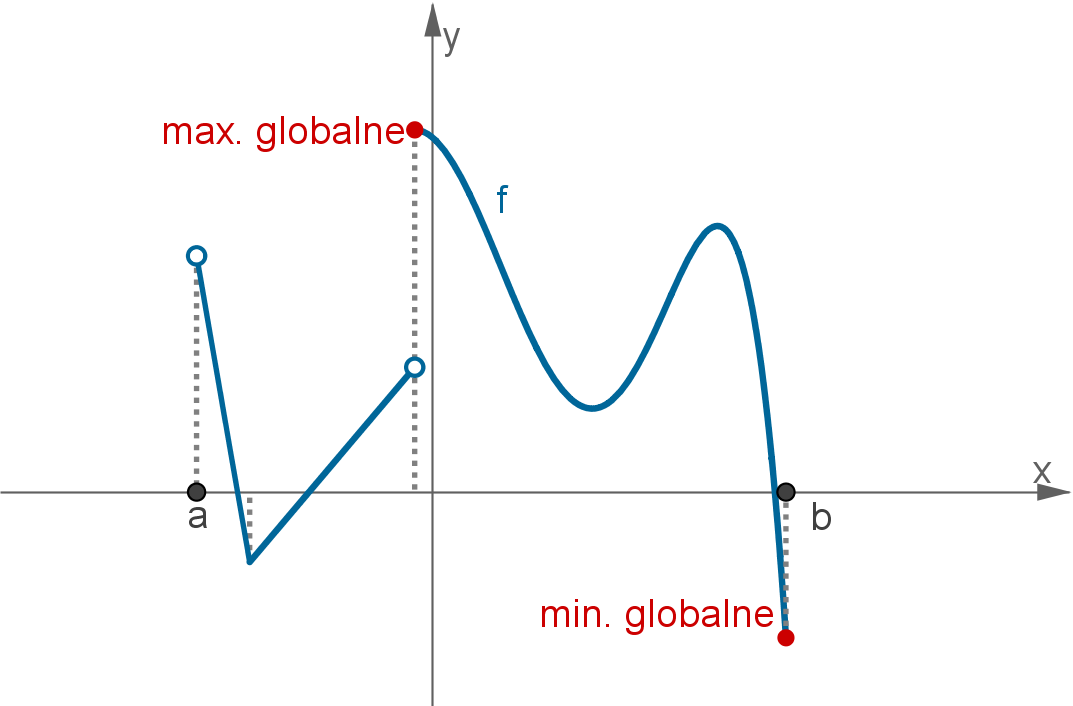
Z twierdzenia Weierstrassa wynika, iż każda funkcja ciągła na przedziale domkniętym posiada w tym przedziale ekstrema globalne. Ekstremum globalne może być osiągnięte wewnątrz tego przedziału (jest to wtedy jednocześnie ekstremum lokalne) lub w punkcie brzegowym przedziału. Stąd wynika
Metoda wyznaczania ekstremów globalnych funkcji ciągłej  na przedziale domkniętym
na przedziale domkniętym ![[a,b] [a,b]](https://port.edu.p.lodz.pl/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.png) :
:
- w przedziale
 znajdujemy punkty
znajdujemy punkty 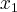 ,
,  ,
, 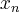 , w których funkcja może mieć ekstrema lokalne, czyli punkty będące rozwiązaniami równania
, w których funkcja może mieć ekstrema lokalne, czyli punkty będące rozwiązaniami równania  lub punkty, w których pochodna nie istnieje,
lub punkty, w których pochodna nie istnieje, - obliczamy wartości funkcji w punktach:
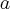 ,
, 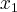 ,
,  ,
, 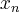 ,
, 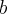 , czyli
, czyli
- największa z liczb
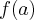 ,
, 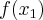 ,
,  ,
, 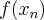 ,
, 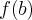 jest maksimum globalnym, a najmniejsza ‒ minimum globalnym funkcji
jest maksimum globalnym, a najmniejsza ‒ minimum globalnym funkcji  na przedziale domkniętym
na przedziale domkniętym ![[a,b] [a,b]](https://port.edu.p.lodz.pl/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
Przykłady
Wyznaczymy najmniejszą i największą wartość (ekstrema globalne) funkcji 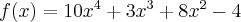 na przedziale
na przedziale ![\left[-1,2\right] \left[-1,2\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/36e0c00681a7b9d8a5526b7f5f8868ec.png) .
.
Wyznaczymy najpierw punkty wewnątrz przedziału, w których funkcja może mieć ekstrema lokalne.
Funkcja  jest różniczkowalna w każdym punkcie przedziału
jest różniczkowalna w każdym punkcie przedziału  , zatem punkt
, zatem punkt  jest jedynym punktem w tym przedziale, w którym funkcja może mieć ekstremum lokalne.
jest jedynym punktem w tym przedziale, w którym funkcja może mieć ekstremum lokalne.
Obliczymy teraz wartości funkcji w punktach, w których  może osiągnąć ekstrema globalne, czyli punkcie
może osiągnąć ekstrema globalne, czyli punkcie  oraz w punktach będących krańcami podanego przedziału:
oraz w punktach będących krańcami podanego przedziału:
Zatem w przedziale ![\left[-1,2\right] \left[-1,2\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/36e0c00681a7b9d8a5526b7f5f8868ec.png) największą wartość (maksimum globalne) dana funkcja przyjmuje dla
największą wartość (maksimum globalne) dana funkcja przyjmuje dla  i wartość ta jest równa
i wartość ta jest równa 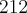 , najmniejszą wartość (minimum globalne) przyjmuje dla
, najmniejszą wartość (minimum globalne) przyjmuje dla  i wartość jest równa
i wartość jest równa  .
.
Możemy też zapisać:
Wyznaczymy najmniejszą i największą wartość (ekstrema globalne) funkcji  na przedziale
na przedziale ![\left[-\sqrt3,\sqrt3\right] \left[-\sqrt3,\sqrt3\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/b1297a8d5a2ce17fc2e847c64b504bf9.png) .
.
Wyznaczymy najmniejszą i największą wartość (ekstrema globalne) funkcji 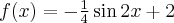 na przedziale
na przedziale ![\left[-\frac\pi2,\frac{3\pi}4\right] \left[-\frac\pi2,\frac{3\pi}4\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/a6499fbe992129b76ad723a4a416c17c.png) .
.
Wyznaczymy najpierw punkty wewnątrz przedziału, w których funkcja może mieć ekstrema lokalne.
Funkcja  jest różniczkowalna w każdym punkcie przedziału
jest różniczkowalna w każdym punkcie przedziału 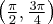 , zatem jedynymi punktami należącymi do tego przedziału, w których funkcja może mieć ekstrema lokalne są:
, zatem jedynymi punktami należącymi do tego przedziału, w których funkcja może mieć ekstrema lokalne są:  ,
,  .
.
Obliczymy teraz wartości funkcji w wyznaczonych wyżej punktach oraz w punktach, które są krańcami podanego przedziału.
Zatem w przedziale ![\left[-\frac\pi2,\frac{3\pi}4\right] \left[-\frac\pi2,\frac{3\pi}4\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/a6499fbe992129b76ad723a4a416c17c.png) największą wartość (maksimum globalne) dana funkcja przyjmuje dla
największą wartość (maksimum globalne) dana funkcja przyjmuje dla  ,
, 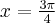 i wartość ta jest równa
i wartość ta jest równa 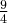 , najmniejszą wartość (minimum globalne) przyjmuje dla
, najmniejszą wartość (minimum globalne) przyjmuje dla  i wartość ta jest równa
i wartość ta jest równa  .
.
Wyznaczymy najmniejszą i największą wartość (ekstrema globalne) funkcji  na przedziale
na przedziale ![\left[-2,1\right] \left[-2,1\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/433b65bbd2fe21fcc67ec374215ff1c8.png) .
.
Wyznaczymy najpierw punkty wewnątrz przedziału, w których funkcja może mieć ekstrema lokalne.
Funkcja  jest różniczkowalna w każdym punkcie przedziału
jest różniczkowalna w każdym punkcie przedziału  , zatem punkty
, zatem punkty  ,
,  są jedynymi w tym przedziale, w których funkcja może mieć ekstrema lokalne.
są jedynymi w tym przedziale, w których funkcja może mieć ekstrema lokalne.
Obliczymy teraz wartości funkcji w wyznaczonych wyżej punktach oraz w punktach, które są krańcami podanego przedziału.
Zatem w przedziale ![\left[-2,1\right] \left[-2,1\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/433b65bbd2fe21fcc67ec374215ff1c8.png) największą wartość (maksimum globalne) dana funkcja przyjmuje dla
największą wartość (maksimum globalne) dana funkcja przyjmuje dla 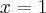 i wartość ta jest równa
i wartość ta jest równa  , najmniejszą wartość (minimum globalne) przyjmuje dla
, najmniejszą wartość (minimum globalne) przyjmuje dla  i wartość ta jest równa
i wartość ta jest równa  .
.
Wyznaczymy najmniejszą i największą wartość (ekstrema globalne) funkcji  na przedziale
na przedziale ![\left[e^{-2},e^2\right] \left[e^{-2},e^2\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/edeca57f6f48fa40bf719bc7bd30b885.png) .
.
Wyznaczymy najpierw punkty wewnątrz przedziału, w których funkcja może mieć ekstrema lokalne.
Funkcja  jest różniczkowalna w każdym punkcie przedziału
jest różniczkowalna w każdym punkcie przedziału  , zatem punkty
, zatem punkty  ,
,  są jedynymi w tym przedziale, w których funkcja może mieć ekstrema lokalne.
są jedynymi w tym przedziale, w których funkcja może mieć ekstrema lokalne.
Obliczymy teraz wartości funkcji w wyznaczonych wyżej punktach oraz w punktach, które są krańcami podanego przedziału.
Zatem w przedziale ![\left[e^{-2},e^2\right] \left[e^{-2},e^2\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/edeca57f6f48fa40bf719bc7bd30b885.png) największą wartość (maksimum globalne) dana funkcja przyjmuje dla
największą wartość (maksimum globalne) dana funkcja przyjmuje dla  i wartość ta jest równa
i wartość ta jest równa  , najmniejszą wartość (minimum globalne) przyjmuje w punkcie
, najmniejszą wartość (minimum globalne) przyjmuje w punkcie  i wartość ta jest równa
i wartość ta jest równa  .
.
Wyznaczymy najmniejszą i największą wartość (ekstrema globalne) funkcji ![f(x)=6x-9\sqrt[3]{x^2} f(x)=6x-9\sqrt[3]{x^2}](https://port.edu.p.lodz.pl/filter/tex/pix.php/eb62f0d910c81568987a04befe5e023a.png) na przedziale
na przedziale ![\left[-1,\sqrt{8}\right] \left[-1,\sqrt{8}\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/373666af5a368bfec033967341dff2ac.png) .
.
Wyznaczymy najpierw punkty wewnątrz przedziału, w których funkcja może mieć ekstrema lokalne.
Ponadto funkcja  nie jest różniczkowalna w
nie jest różniczkowalna w  (można pokazać, że
(można pokazać, że  oraz
oraz  ). To oznacza, że
). To oznacza, że  może mieć ekstrema lokalne jedynie w punktach
może mieć ekstrema lokalne jedynie w punktach  i
i 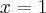 .
.
Obliczymy teraz wartości funkcji w wyznaczonych wyżej punktach oraz w punktach, które są krańcami podanego przedziału.
Zatem w przedziale ![\left[-1,\sqrt{8}\right] \left[-1,\sqrt{8}\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/373666af5a368bfec033967341dff2ac.png) największą wartość (maksimum globalne) dana funkcja przyjmuje dla
największą wartość (maksimum globalne) dana funkcja przyjmuje dla  i wartość ta jest równa
i wartość ta jest równa  , najmniejszą wartość (minimum globalne) przyjmuje dla
, najmniejszą wartość (minimum globalne) przyjmuje dla  i wartość ta jest równa
i wartość ta jest równa  .
.
Ćwiczenia interaktywne, cz.1
Przypomnij sobie:
• definicje ekstremów globalnych • metodę wyznaczania ekstremów globalnych
Przyporządkuj podane funkcje do odpowiedniej grupy.
Przeciągnij poprawne odpowiedzi w odpowiednie pola.
Ćwiczenia interaktywne, cz.2
Przypomnij sobie:
• definicje ekstremów globalnych • metodę wyznaczania ekstremów globalnych
Wyznacz ekstrema globalne funkcji określonej wzorem 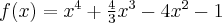 na przedziale
na przedziale ![[-1,3] [-1,3]](https://port.edu.p.lodz.pl/filter/tex/pix.php/82ed59f03b26c4e8173e2aa9cfa7ef87.png) .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz ekstrema globalne funkcji określonej wzorem 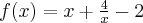 na przedziale
na przedziale ![[1,8] [1,8]](https://port.edu.p.lodz.pl/filter/tex/pix.php/27eea7e95ff813cca3f2668ed27b7bb5.png) .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz ekstrema globalne funkcji określonej wzorem 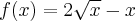 na przedziale
na przedziale ![[0,9] [0,9]](https://port.edu.p.lodz.pl/filter/tex/pix.php/ed4b9ac97624a64f5e34ea5e30246fa9.png) .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz ekstrema globalne funkcji określonej wzorem 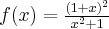 na przedziale
na przedziale ![[-2,2] [-2,2]](https://port.edu.p.lodz.pl/filter/tex/pix.php/98fab4cc523eb62bb9cf3a4fbefb7a69.png) .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz ekstrema globalne funkcji określonej wzorem 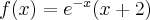 na przedziale
na przedziale ![[-3,0] [-3,0]](https://port.edu.p.lodz.pl/filter/tex/pix.php/f71e38c0b66d48ef317e099224862b62.png) .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
4.4 Zadania
Wyznacz ekstrema lokalne i przedziały monotoniczności funkcji określonej wzorem:
- Dziedziną funkcji jest zbiór
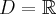 . Funkcja jest rosnąca na każdym z przedziałów:
. Funkcja jest rosnąca na każdym z przedziałów:  ,
, 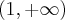 , malejąca na przedziale
, malejąca na przedziale 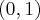 , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne,  , w punkcie
, w punkcie 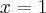 funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 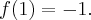
- Dziedziną funkcji jest zbiór
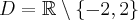 . Funkcja jest rosnąca na każdym z przedziałów:
. Funkcja jest rosnąca na każdym z przedziałów: 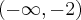 ,
, 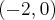 , malejąca na każdym z przedziałów:
, malejąca na każdym z przedziałów: 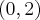 ,
,  , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 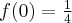 .
. - Dziedziną funkcji jest zbiór
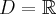 . Funkcja jest malejąca na każdym z przedziałów:
. Funkcja jest malejąca na każdym z przedziałów: 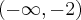 ,
,  , rosnąca na przedziale
, rosnąca na przedziale 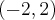 , w punkcie
, w punkcie  funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 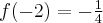 , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 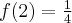 .
. - Dziedziną funkcji jest zbiór
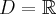 . Funkcja jest rosnąca na każdym z przedziałów:
. Funkcja jest rosnąca na każdym z przedziałów: 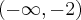 ,
,  , malejąca na przedziale
, malejąca na przedziale 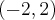 , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 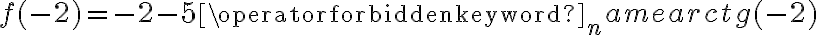 , w punkcie
, w punkcie  funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 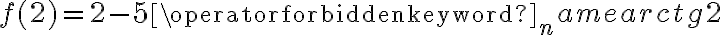 .
.
Wyznacz ekstrema lokalne i przedziały monotoniczności funkcji określonej wzorem:
- Dziedziną funkcji jest zbiór
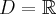 . Funkcja jest rosnąca w całej swojej dziedzinie.
. Funkcja jest rosnąca w całej swojej dziedzinie. - Funkcja jest rosnąca na każdym z przedziałów:
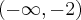 ,
,  , malejąca na przedziale
, malejąca na przedziale 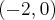 , w punkcie
, w punkcie  funkcja ma minimum lokalne, o wartości
funkcja ma minimum lokalne, o wartości  , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 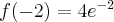 .
. - Dziedziną funkcji jest zbiór
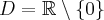 . Funkcja jest rosnąca na każdym z przedziałów:
. Funkcja jest rosnąca na każdym z przedziałów:  ,
, 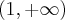 , malejąca na przedziale
, malejąca na przedziale 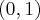 , w punkcie
, w punkcie 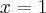 funkcja ma minimum lokalne,
funkcja ma minimum lokalne,  .
. - Dziedziną funkcji jest zbiór
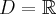 . Funkcja jest rosnąca na każdym z przedziałów:
. Funkcja jest rosnąca na każdym z przedziałów:  ,
, 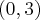 , malejąca na przedziale
, malejąca na przedziale 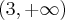 , w punkcie j
, w punkcie j 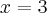 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 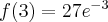 .
.
Wyznacz ekstrema lokalne i przedziały monotoniczności funkcji określonej wzorem:
- Dziedziną funkcji jest zbiór
 . Funkcja jest rosnąca na przedziale
. Funkcja jest rosnąca na przedziale 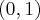 , malejąca na przedziale
, malejąca na przedziale 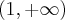 , w punkcie
, w punkcie 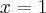 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 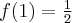 .
. - Dziedziną funkcji jest zbiór
 . Funkcja jest rosnąca na przedziale
. Funkcja jest rosnąca na przedziale 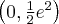 , malejąca na przedziale
, malejąca na przedziale 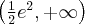 , w punkcie
, w punkcie 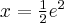 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 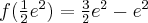 .
. - Dziedziną funkcji jest zbiór
 . Funkcja jest rosnąca na każdym z przedziałów:
. Funkcja jest rosnąca na każdym z przedziałów: 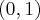 ,
, 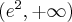 , malejąca na przedziale
, malejąca na przedziale 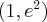 , w punkcie
, w punkcie 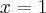 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 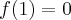 , w punkcie
, w punkcie 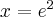 funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 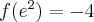 .
.
Wyznacz asymptoty, ekstrema lokalne, przedziały monotoniczności oraz naszkicuj wykres funkcji określonej wzorem:
- Dziedziną funkcji jest zbiór
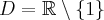 . Funkcja ma asymptotę pionową obustronną
. Funkcja ma asymptotę pionową obustronną 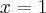 , asymptotę ukośną
, asymptotę ukośną 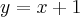 w
w 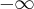 i w
i w 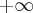 . Funkcja jest malejąca na każdym z przedziałów:
. Funkcja jest malejąca na każdym z przedziałów: 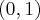 ,
, 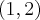 , rosnąca na każdym z przedziałów:
, rosnąca na każdym z przedziałów:  ,
,  , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne,  , w punkcie
, w punkcie  funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 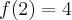 .
.
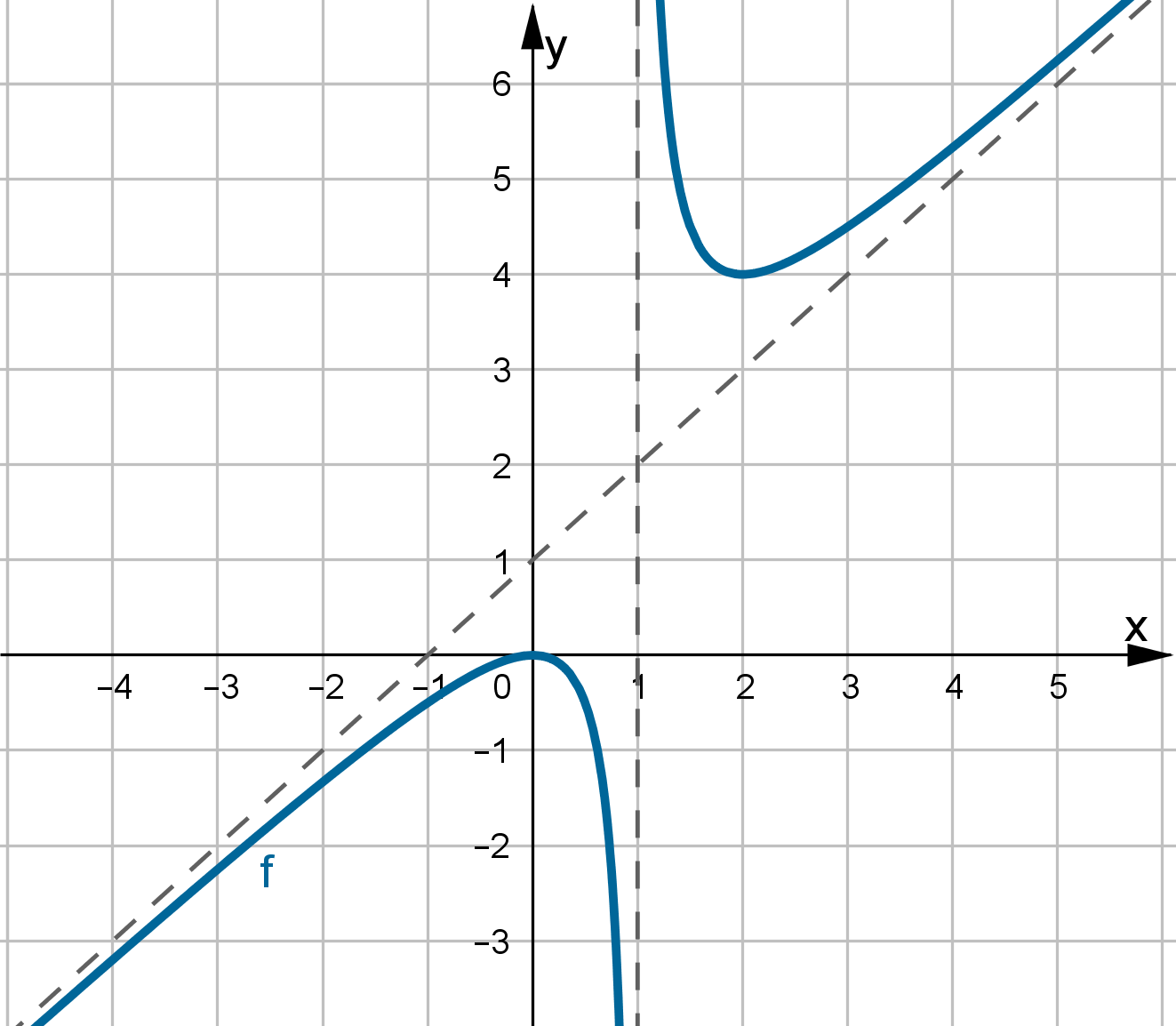
- Dziedziną funkcji jest zbiór
 . Funkcja ma asymptotę poziomą
. Funkcja ma asymptotę poziomą  w
w  . Funkcja jest rosnąca na przedziale
. Funkcja jest rosnąca na przedziale 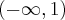 , malejąca na przedziale
, malejąca na przedziale 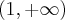 , w punkcie
, w punkcie 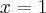 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 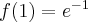 .
.
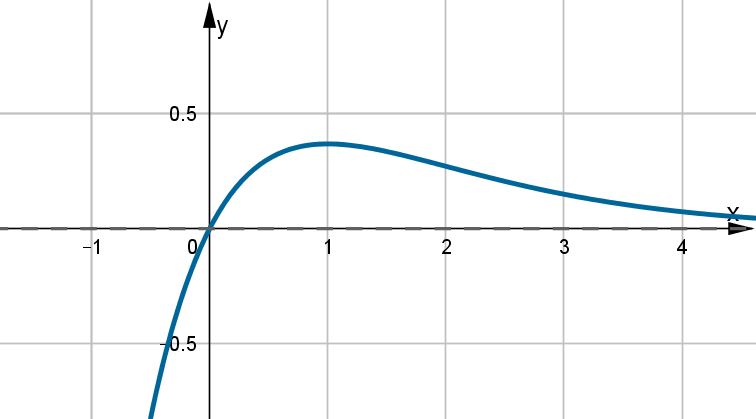
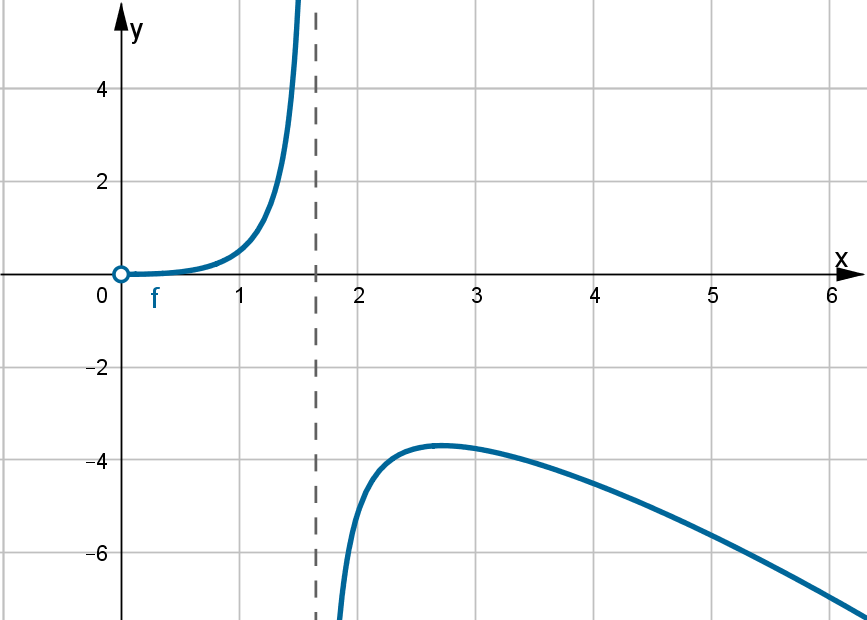
- Dziedziną funkcji jest zbiór
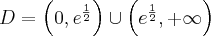 . Funkcja ma asymptotę pionową obustronną
. Funkcja ma asymptotę pionową obustronną 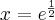 . Funkcja jest rosnąca na każdym z przedziałów
. Funkcja jest rosnąca na każdym z przedziałów 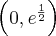 ,
,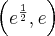 , malejąca na przedziale
, malejąca na przedziale 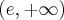 , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 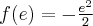 .
.
5. Wypukłość, wklęsłość funkcji, punkty przegięcia
W tym rozdziale poznamy:
- definicję funkcji wypukłej/wklęsłej w punkcie i na przedziale
- warunki wystarczające
 wypukłości/wklęsłości funkcji na przedziale
wypukłości/wklęsłości funkcji na przedziale - definicję punktu przegięcia wykresu funkcji
- warunek konieczny
 istnienia punktu przegięcia
istnienia punktu przegięcia - warunek wystarczający istnienia punktu przegięcia.
Nauczymy się jak:
- wyznaczać przedziały wypukłości/wklęsłości funkcji wykorzystując drugą pochodną
- badać istnienie punktów przegięcia w oparciu o warunki wystarczające.
5.1 Badanie wypukłości i wklęsłości funkcji
W tym rozdziale dostępne są: Teoria, Przykłady, Ćwiczenia interaktywne.
Teoria
Załóżmy, że funkcja  jest różniczkowalna na pewnym otoczeniu punktu
jest różniczkowalna na pewnym otoczeniu punktu  .
.
- wypukłą w punkcie
 , jeżeli istnieje takie sąsiedztwo
, jeżeli istnieje takie sąsiedztwo  punktu
punktu  , że dla każdego
, że dla każdego  zachodzi nierówność
zachodzi nierówność 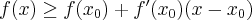 ;
; - wklęsłą w punkcie
 , jeżeli istnieje takie sąsiedztwo
, jeżeli istnieje takie sąsiedztwo  punktu
punktu  , że dla każdego
, że dla każdego  zachodzi nierówność
zachodzi nierówność 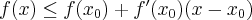 .
.
Jeżeli nierówności w powyższych definicjach są ostre, to funkcja jest odpowiednio ściśle wypukła lub ściśle wklęsła.
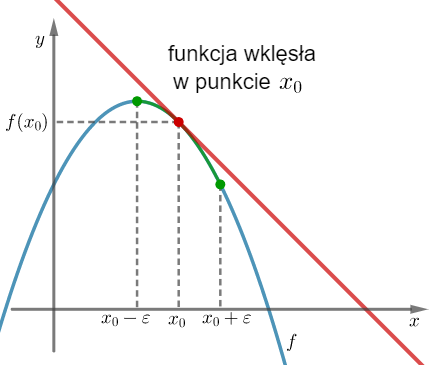
Geometrycznie oznacza to, że funkcja jest wypukła (wklęsła) w punkcie  , jeżeli istnieje takie sąsiedztwo
, jeżeli istnieje takie sąsiedztwo  , że na
, że na  wykres funkcji leży powyżej (poniżej) lub pokrywa się z prostą styczną do wykresu tej funkcji w punkcie
wykres funkcji leży powyżej (poniżej) lub pokrywa się z prostą styczną do wykresu tej funkcji w punkcie  .
.
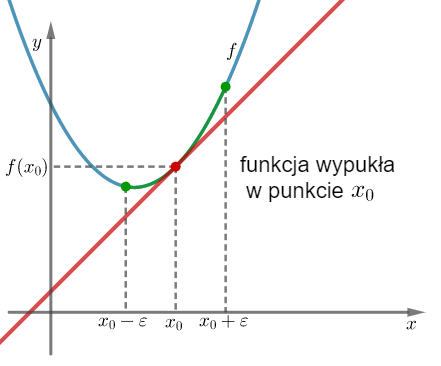
Geometrycznie oznacza to, że funkcja jest wypukła (wklęsła) na przedziale  , jeżeli na dowolnym przedziale
, jeżeli na dowolnym przedziale 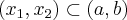 wykres funkcji leży pod (nad) lub pokrywa się z prostą sieczną przechodzącą przez punkty
wykres funkcji leży pod (nad) lub pokrywa się z prostą sieczną przechodzącą przez punkty 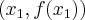 i
i 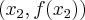 .
.
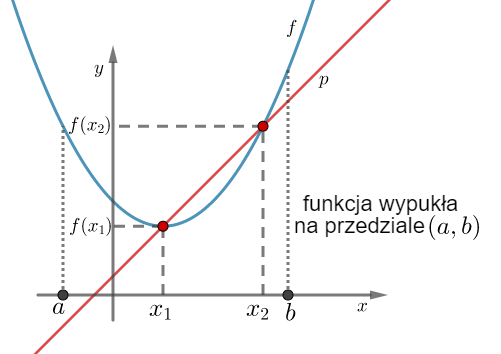
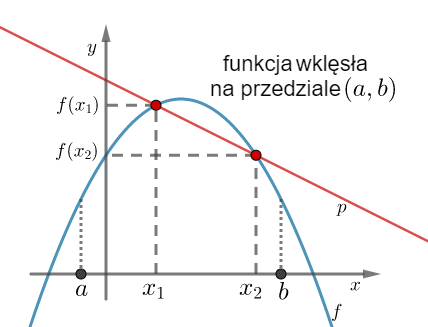
Przykłady
Ćwiczenia interaktywne, cz.1
Przypomnij sobie:
• definicję funkcji wypukłej w punkcie • definicję funkcji wklęsłej w punkcie • definicję funkcji wypukłej na przedziale • definicję funkcji wklęsłej na przedziale • warunki wystarczające wypukłości/wklęsłości funkcji
Dokończ poprawnie zdanie wybierając jedną z odpowiedzi.
Zastanów się nad wypukłością/wklęsłością przedstawionych funkcji na poszczególnych przedziałach dziedziny.
Dokończ zdanie wybierając poprawne odpowiedzi.
Uzupełnij luki.
Połącz w pary: wzór i własność funkcji.
Przyciągnij wzory do własności.
Połącz w pary: wykres i własność funkcji.
Ćwiczenia interaktywne, cz.2
Przypomnij sobie:
• definicję funkcji wypukłej w punkcie • definicję funkcji wklęsłej w punkcie • definicję funkcji wypukłej na przedziale • definicję funkcji wklęsłej na przedziale • warunki wystarczające wypukłości/wklęsłości funkcji
Wyznacz przedziały wypukłości/wklęsłości funkcji  określonej wzorem
określonej wzorem  .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz przedziały wypukłości/wklęsłości funkcji  określonej wzorem
określonej wzorem  .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
5.2 Punkty przegięcia wykresu funkcji
W tym rozdziale dostępne są: Teoria, Przykłady, Ćwiczenia interaktywne.
Teoria
Przykłady
Dziedziną funkcji jest zbiór  .
.
Obliczamy pierwszą i drugą pochodną funkcji  :
:
Zauważmy, że dla każdego  pochodna rzędu drugiego jest dodatnia, zatem nie jest spełniony warunek konieczny istnienia punktu przegięcia i wykres funkcji
pochodna rzędu drugiego jest dodatnia, zatem nie jest spełniony warunek konieczny istnienia punktu przegięcia i wykres funkcji  nie posiada punktów przegięcia.
nie posiada punktów przegięcia.
Funkcja  jest wielomianem, jest więc określona dla każdego
jest wielomianem, jest więc określona dla każdego  .
.
Obliczamy pierwszą i drugą pochodną funkcji  :
:
i przyrównujemy drugą pochodną do zera:
Stąd wynika, że wykres funkcji  może mieć tylko jeden punkt przegięcia. Dalej o istnieniu punktu przegięcia rozstrzygamy stosując jedną z dwóch metod podanych poniżej.
może mieć tylko jeden punkt przegięcia. Dalej o istnieniu punktu przegięcia rozstrzygamy stosując jedną z dwóch metod podanych poniżej.
1 sposób (wykorzystamy I warunek wystarczający istnienia punktu przegięcia)
Badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie a gdzie ujemne:
oraz
Stąd wynika, że  dla
dla 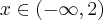 (a zatem także dla pewnego lewostronnego sąsiedztwa 2) oraz
(a zatem także dla pewnego lewostronnego sąsiedztwa 2) oraz  dla
dla  (przedział ten można potraktować jako prawostronne sąsiedztwo 2). Zatem punkt
(przedział ten można potraktować jako prawostronne sąsiedztwo 2). Zatem punkt  jest punktem przegięcia wykresu funkcji
jest punktem przegięcia wykresu funkcji  .
.
Metodę tę stosujemy najczęściej wtedy, gdy jednocześnie mamy wyznaczyć przedziały wklęsłości i wypukłości funkcji  .
.
2 sposób (wykorzystamy II warunek wystarczający istnienia punktu przegięcia)
Funkcja  jest określona dla każdego
jest określona dla każdego  .
.
Obliczamy pierwszą i drugą pochodną funkcji  :
:
i przyrównujemy drugą pochodną do zera:
Ponieważ  dla każdego
dla każdego  , więc
, więc  dla
dla  . Oczywiście
. Oczywiście  należy do dziedziny funkcji. Dalej badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie a gdzie ujemne:
należy do dziedziny funkcji. Dalej badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie a gdzie ujemne:
oraz
Ponieważ  dla
dla  , więc funkcja jest wypukła na przedziale
, więc funkcja jest wypukła na przedziale  . Ponieważ
. Ponieważ  dla
dla  , więc funkcja jest wklęsła na przedziale
, więc funkcja jest wklęsła na przedziale 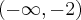 . Na mocy I warunku wystarczającego istnienia punktu przegięcia punkt
. Na mocy I warunku wystarczającego istnienia punktu przegięcia punkt  jest punktem przegięcia wykresu funkcji
jest punktem przegięcia wykresu funkcji  .
.
Uzyskane wyniki i odpowiedź (uwzględniając również przedziały wypukłości i wklęsłości badanej funkcji) najczęściej zapisujemy w postaci tabeli.

Zauważmy, że funkcja  jest określona dla każdego
jest określona dla każdego  .
.
Obliczamy pierwszą i drugą pochodną funkcji  :
:
i przyrównujemy drugą pochodną do zera:
Stąd wynika, że wykres funkcji  może mieć tylko jeden punkt przegięcia. Dalej badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie a gdzie ujemne:
może mieć tylko jeden punkt przegięcia. Dalej badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie a gdzie ujemne:
oraz
Wyniki umieszczamy w tabeli:

Funkcja jest wypukła na przedziale  , wklęsła na przedziale
, wklęsła na przedziale  , a punkt
, a punkt 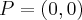 jest punktem przegięcia wykresu funkcji
jest punktem przegięcia wykresu funkcji  .
.
Ćwiczenia interaktywne, cz.1
Przypomnij sobie:
• definicję punktu przegięcia • warunek konieczny istnienia punktu przegięcia • I warunek wystarczający istnienia punktu przegięcia • II warunek wystarczający istnienia punktu przegięcia
Zastanów się, jakie punkty przegięcia posiadają funkcje o przedstawionych wykresach.
Przyporządkuj podane funkcje do odpowiedniej grupy.
Dopasuj do funkcji punkty przegięcia ich wykresów.
Zaznacz punkty przegięcia wykresu funkcji.
Ćwiczenia interaktywne, cz.2
Przypomnij sobie:
• definicję punktu przegięcia • warunek konieczny istnienia punktu przegięcia • I warunek wystarczający istnienia punktu przegięcia • II warunek wystarczający istnienia punktu przegięcia
Wyznacz przedziały wypukłości/wklęsłości i punkty przegięcia wykresu funkcji  określonej wzorem
określonej wzorem 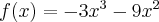 .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz przedziały wypukłości/wklęsłości i punkty przegięcia wykresu funkcji  określonej wzorem
określonej wzorem  .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz przedziały wypukłości/wklęsłości i punkty przegięcia wykresu funkcji  określonej wzorem
określonej wzorem  .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
5.3 Zadania
 Punkt przegięcia:
Punkt przegięcia: 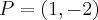 . Funkcja jest wypukła na przedziale
. Funkcja jest wypukła na przedziale 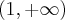 , wklęsła na przedziale
, wklęsła na przedziale 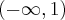 .
.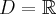 . Punkty przegięcia:
. Punkty przegięcia: 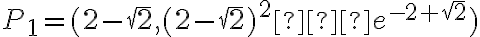 ,
, 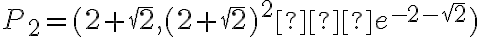 . Funkcja jest wypukła na przedziałach
. Funkcja jest wypukła na przedziałach 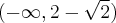 ,
, 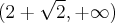 , wklęsła na przedziale
, wklęsła na przedziale 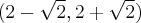 .
.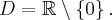 Brak punktów przegięcia. Funkcja jest wypukła na przedziale
Brak punktów przegięcia. Funkcja jest wypukła na przedziale  , wklęsła na przedziale
, wklęsła na przedziale  .
. . Punkt przegięcia:
. Punkt przegięcia: 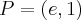 . Funkcja jest wypukła na przedziale
. Funkcja jest wypukła na przedziale 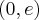 , wklęsła na przedziale
, wklęsła na przedziale 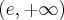 .
.
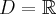 . Punkty przegięcia:
. Punkty przegięcia: 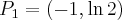 ,
, 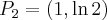 . Funkcja jest wypukła na przedziale
. Funkcja jest wypukła na przedziale 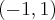 , wklęsła na przedziałach
, wklęsła na przedziałach 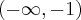 ,
, 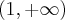 .
. Punkt przegięcia:
Punkt przegięcia: 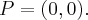 Funkcja jest wypukła na przedziale
Funkcja jest wypukła na przedziale 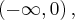 wklęsła na przedziale
wklęsła na przedziale 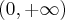 .
.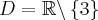 . Brak punktów przegięcia. Funkcja jest wypukła na przedziale
. Brak punktów przegięcia. Funkcja jest wypukła na przedziale 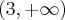 , wklęsła na przedziale
, wklęsła na przedziale 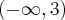 .
.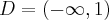 . Brak punktów przegięcia. Funkcja jest wklęsła na na przedziale
. Brak punktów przegięcia. Funkcja jest wklęsła na na przedziale 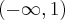 .
.
6. Badanie przebiegu zmienności funkcji
W tym rozdziale nauczymy się badać przebieg zmienności funkcji wykorzystując rachunek różniczkowy.
Teoria
Badanie przebiegu zmienności funkcji  jest zadaniem złożonym i obejmuje kilka etapów:
jest zadaniem złożonym i obejmuje kilka etapów:
- wyznaczenie dziedziny funkcji,
- wyznaczenie asymptot wykresu funkcji,
- wyznaczenie przedziałów monotoniczności i ekstremów lokalnych funkcji (badanie pierwszej pochodnej funkcji: rozwiązanie równania
 oraz nierówności
oraz nierówności  i
i  ),
), - wyznaczenie przedziałów wypukłości i wklęsłości oraz punktów przegięcia funkcji (badanie drugiej pochodnej funkcji: rozwiązanie równania
 oraz nierówności
oraz nierówności  i
i 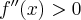 ),
), - zestawienie uzyskanych wyników w tabeli i sporządzenie na tej podstawie wykresu funkcji.
Przykłady
-
Wyznaczymy asymptoty wykresu funkcji
 . Obliczamy w tym celu granice funkcji na krańcach jej dziedziny:
. Obliczamy w tym celu granice funkcji na krańcach jej dziedziny:Zatem prosta o równaniu
 jest asymptotą poziomą wykresu funkcji w
jest asymptotą poziomą wykresu funkcji w 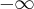 i
i 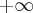 .
.Wykres funkcji nie ma asymptot pionowych.
-
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji
 . Obliczamy w tym celu pochodną funkcji.
. Obliczamy w tym celu pochodną funkcji.Wyznaczamy punkty stacjonarne funkcji:
Badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Zauważmy najpierw, że
 dla każdego
dla każdego  , zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia  . Mamy więc:
. Mamy więc:Zatem funkcja jest malejąca na przedziale
 , rosnąca na przedziale
, rosnąca na przedziale  .
.Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie
 funkcja ma minimum lokalne równe
funkcja ma minimum lokalne równe  .
. -
Wyznaczymy przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji
 . Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie
. Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie  .
.Badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie , a gdzie ujemne. Zauważmy, że
 dla każdego
dla każdego  , zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia  .
.Zatem funkcja jest wypukła na przedziale
 , wklęsła na przedziałach
, wklęsła na przedziałach  ,
,  . Punkty
. Punkty  ,
, 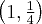 są punktami przegięcia wykresu funkcji.
są punktami przegięcia wykresu funkcji. -
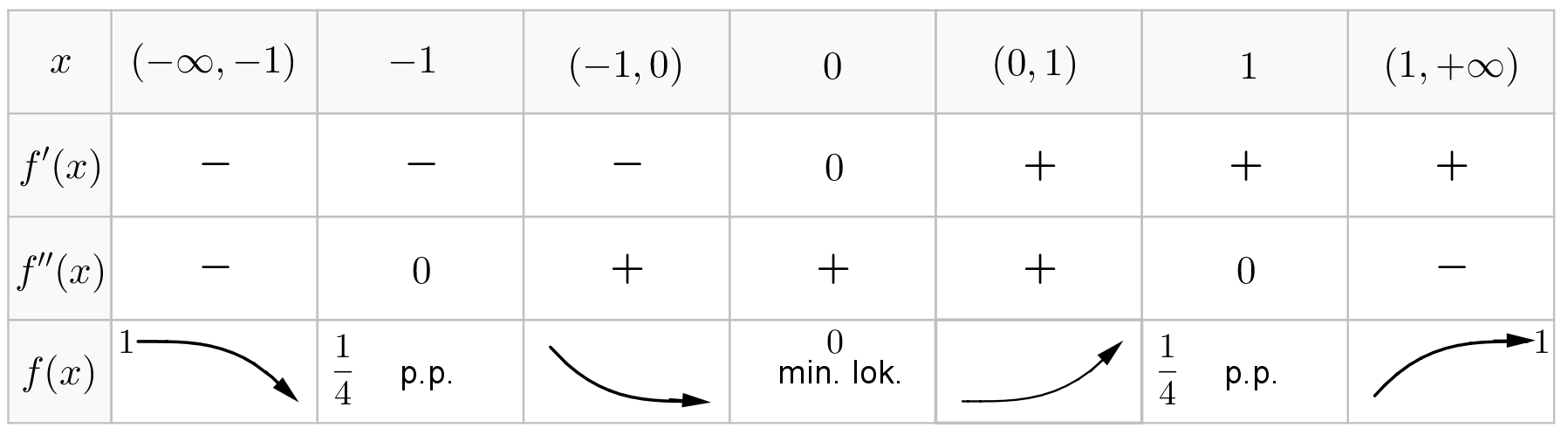
Tabelka przebiegu zmienności funkcji
 .
.
-
Wykres funkcji
 . Zaczynamy od narysowania asymptot, następnie zaznaczamy wyznaczone punkty specjalne (punkty ekstremalne i punkty przegięcia) oraz szkicujemy wykres funkcji na podstawie tabeli.
. Zaczynamy od narysowania asymptot, następnie zaznaczamy wyznaczone punkty specjalne (punkty ekstremalne i punkty przegięcia) oraz szkicujemy wykres funkcji na podstawie tabeli.
- Dziedziną funkcji
 jest zbiór
jest zbiór  .
. - Wyznaczymy asymptoty wykresu funkcji
 . Obliczymy w tym celu granice funkcji na krańcach jej dziedziny:
. Obliczymy w tym celu granice funkcji na krańcach jej dziedziny:
Zatem funkcja ma asymptotę pionową prawostronną
 .
.Zatem prosta o równaniu
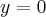 jest asymptotą poziomą wykresu funkcji
jest asymptotą poziomą wykresu funkcji  w
w 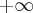 .
. -
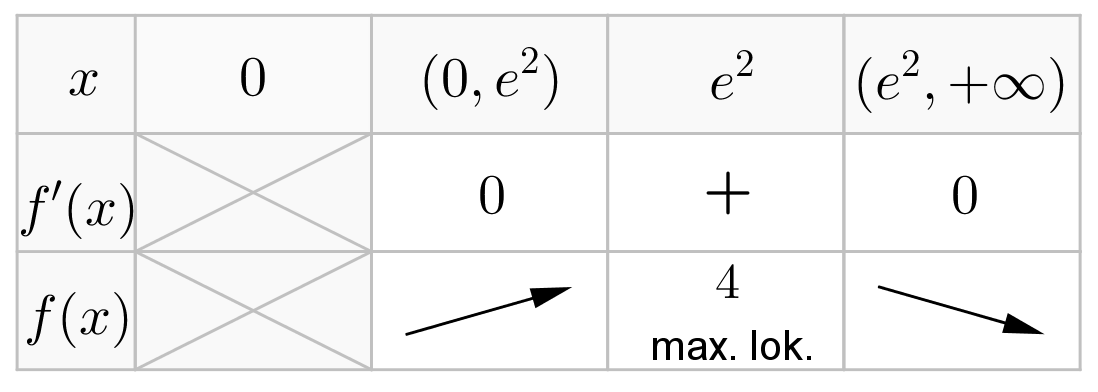
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji
 . Obliczamy w tym celu pochodną funkcji.
. Obliczamy w tym celu pochodną funkcji.Wyznaczamy punkty stacjonarne funkcji:
Badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Zauważmy najpierw, że
 dla każdego
dla każdego  , zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia  . Mamy więc:
. Mamy więc:Zatem funkcja jest rosnąca na przedziale
 , malejąca na przedziale
, malejąca na przedziale  .
.Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie
 funkcja ma maksimum lokalne równe
funkcja ma maksimum lokalne równe  .
. -
Wyznaczymy przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji
 . Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie
. Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie  .
.Badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie , a gdzie ujemne. Zauważmy, że
 dla każdego
dla każdego  , zatem znak drugiej pochodnej funkcji będzie taki sam jak znak wyrażenia
, zatem znak drugiej pochodnej funkcji będzie taki sam jak znak wyrażenia  .
.Zatem funkcja
 jest wklęsła na przedziale
jest wklęsła na przedziale  , wypukła na przedziale
, wypukła na przedziale 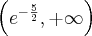 , punkt
, punkt 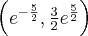 jest punktem przegięcia wykresu funkcji.
jest punktem przegięcia wykresu funkcji. -
Tabelka przebiegu zmienności funkcji
 .
.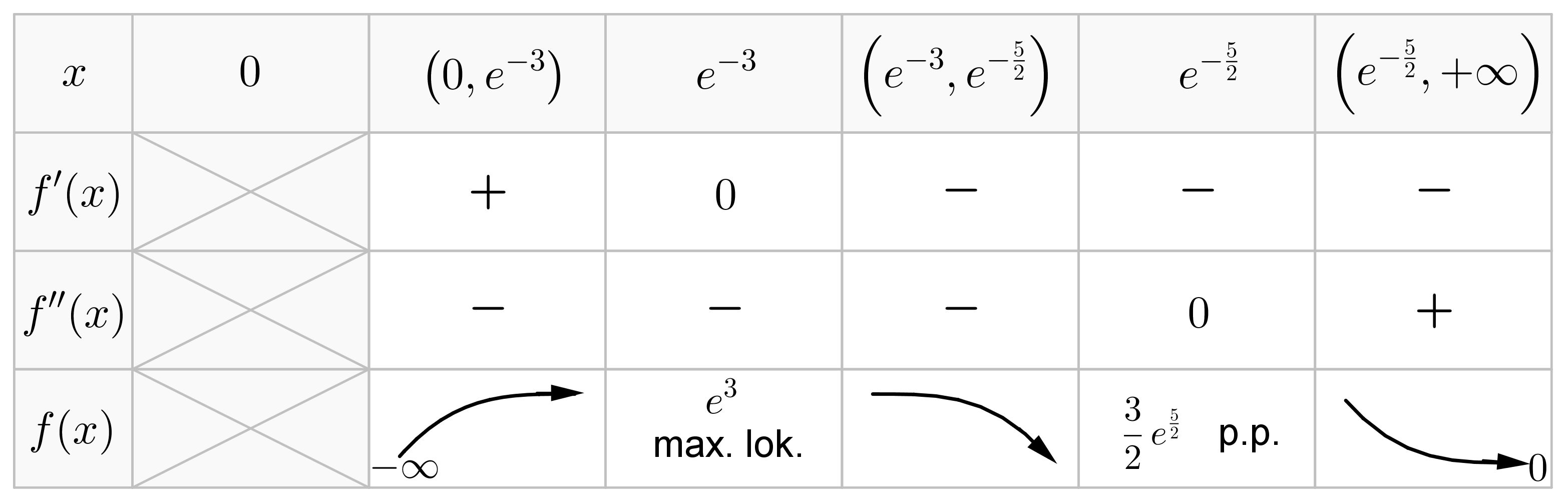
-
Wykres funkcji
 . Zaczynamy od narysowania asymptot, następnie zaznaczamy wyznaczone punkty specjalne (punkty ekstremalne i punkty przegięcia) oraz szkicujemy wykres funkcji na podstawie tabeli.
. Zaczynamy od narysowania asymptot, następnie zaznaczamy wyznaczone punkty specjalne (punkty ekstremalne i punkty przegięcia) oraz szkicujemy wykres funkcji na podstawie tabeli.
- Dziedziną funkcji
 jest zbiór
jest zbiór  .
. -
Wyznaczymy asymptoty wykresu funkcji
 . Obliczymy w tym celu granice funkcji na krańcach jej dziedziny:
. Obliczymy w tym celu granice funkcji na krańcach jej dziedziny:Ponieważ obie policzone powyżej granice są niewłaściwe więc wykres funkcji nie ma symptoty poziomej. Sprawdzamy istnienie asymptot ukośnych wykresu funkcji w
 i
i  .
.Prosta o równaniu
 , czyli
, czyli  jest asymptotą ukośną wykresu funkcji w
jest asymptotą ukośną wykresu funkcji w  .
.Zatem prosta o równaniu
 jest asymptotą ukośną wykresu funkcji w
jest asymptotą ukośną wykresu funkcji w  .
.Podsumowując otrzymujemy, że prosta o równaniu
 jest asymptotą ukośną wykresu funkcji w
jest asymptotą ukośną wykresu funkcji w  , prosta prosta o równaniu
, prosta prosta o równaniu  jest asymptotą ukośną wykresu funkcji w
jest asymptotą ukośną wykresu funkcji w 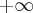 . Wykres funkcji
. Wykres funkcji  nie ma asymptot pionowych.
nie ma asymptot pionowych. -
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji
 . Obliczamy w tym celu pochodną funkcji.
. Obliczamy w tym celu pochodną funkcji.Wyznaczamy punkty stacjonarne funkcji:
Badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Zauważmy najpierw, że
 dla każdego
dla każdego  , zatem znak pochodnej funkcji będzie taki sam jak znak wyrażenia
, zatem znak pochodnej funkcji będzie taki sam jak znak wyrażenia  . Mamy więc:
. Mamy więc:Zatem funkcja jest malejąca na każdym z przedziałów
 ,
, 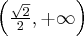 , rosnąca na przedziale
, rosnąca na przedziale  . Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie
. Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie 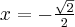 funkcja ma minimum lokalne równe
funkcja ma minimum lokalne równe  , zaś w punkcie
, zaś w punkcie  funkcja ma maksimum lokalne równe
funkcja ma maksimum lokalne równe 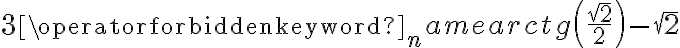 .
. -
Wyznaczymy przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji
 . Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie
. Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie  .
.Badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Zauważmy, że
 dla każdego
dla każdego  , zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia  .
.Zatem funkcja
 jest wypukła na przedziale
jest wypukła na przedziale  , wklęsła na przedziale
, wklęsła na przedziale  , punkt
, punkt  jest punktem przegięcia wykresu funkcji.
jest punktem przegięcia wykresu funkcji. -
Tabelka przebiegu zmienności funkcji
 .
.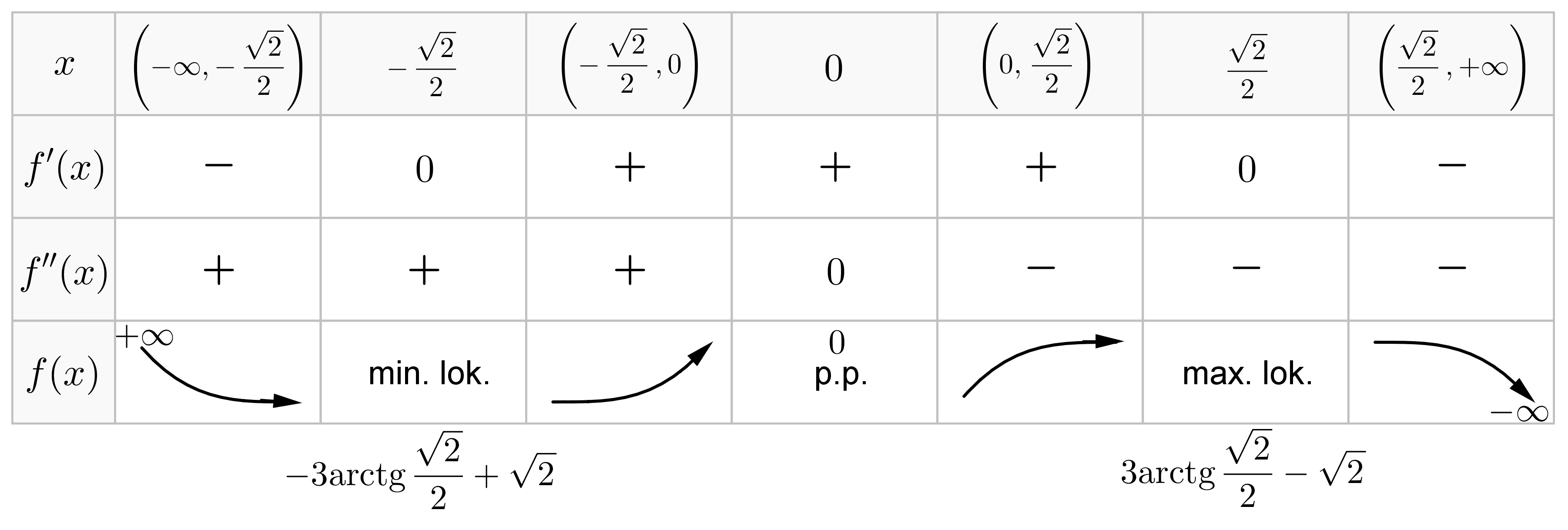
-
Wykres funkcji
 . Zaczynamy od narysowania asymptot, następnie zaznaczamy wyznaczone punkty specjalne (punkty ekstremalne i punkty przegięcia) oraz szkicujemy wykres funkcji na podstawie tabeli.
. Zaczynamy od narysowania asymptot, następnie zaznaczamy wyznaczone punkty specjalne (punkty ekstremalne i punkty przegięcia) oraz szkicujemy wykres funkcji na podstawie tabeli.
Ćwiczenia interaktywne, cz.1
Przypomnij sobie:
• etapy badania przebiegu zmienności funkcji
Uzupełnij.
Uzupełnij.
Uzupełnij.
Uzupełnij.
Niech 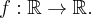 Informacje o pierwszej i drugiej pochodnej funkcji
Informacje o pierwszej i drugiej pochodnej funkcji  zawarte są w poniższej tabeli. Uzupełnij ostatni wiersz tabeli.
zawarte są w poniższej tabeli. Uzupełnij ostatni wiersz tabeli.
Zawartość pustych pól w tabeli możesz zmienić poprzez kliknięcie.
Wybierz rysunki mogące przedstawiać wykres funkcji 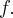
Przenieś wybrane rysunki do obszaru znajdującego się nad nimi.
Ćwiczenia interaktywne, cz.2
Zadania
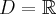 .
. 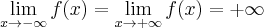 , brak asymptot. Funkcja jest malejąca na przedziale
, brak asymptot. Funkcja jest malejąca na przedziale  , rosnąca na przedziale
, rosnąca na przedziale 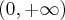 , w punkcie
, w punkcie  funkcja ma minimum lokalne równe
funkcja ma minimum lokalne równe  . Funkcja jest wypukła na każdym z przedziałów:
. Funkcja jest wypukła na każdym z przedziałów: 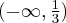 ,
, 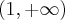 , wklęsła na przedziale
, wklęsła na przedziale  , punkty
, punkty  ,
, 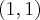 są punktami przegięcia wykresu funkcji.
są punktami przegięcia wykresu funkcji.

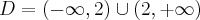 . Wykres funkcji ma asymptotę pionową obustronną
. Wykres funkcji ma asymptotę pionową obustronną  ,
, 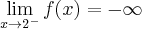 ,
, 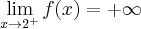 , oraz asymptotę ukośną o równaniu
, oraz asymptotę ukośną o równaniu 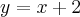 w
w  i
i  . Funkcja jest rosnąca na każdym z przedziałów:
. Funkcja jest rosnąca na każdym z przedziałów:  ,
, 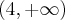 , malejąca na każdym z przedziałów
, malejąca na każdym z przedziałów 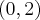 ,
, 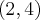 , w punkcie
, w punkcie  funkcja ma maksimum lokalne równe
funkcja ma maksimum lokalne równe  , w punkcie
, w punkcie 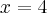 funkcja ma minimum lokalne równe
funkcja ma minimum lokalne równe  . Funkcja jest wklęsła na przedziale
. Funkcja jest wklęsła na przedziale  , wypukła na przedziale
, wypukła na przedziale 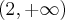 , brak punktów przegięcia.
, brak punktów przegięcia.
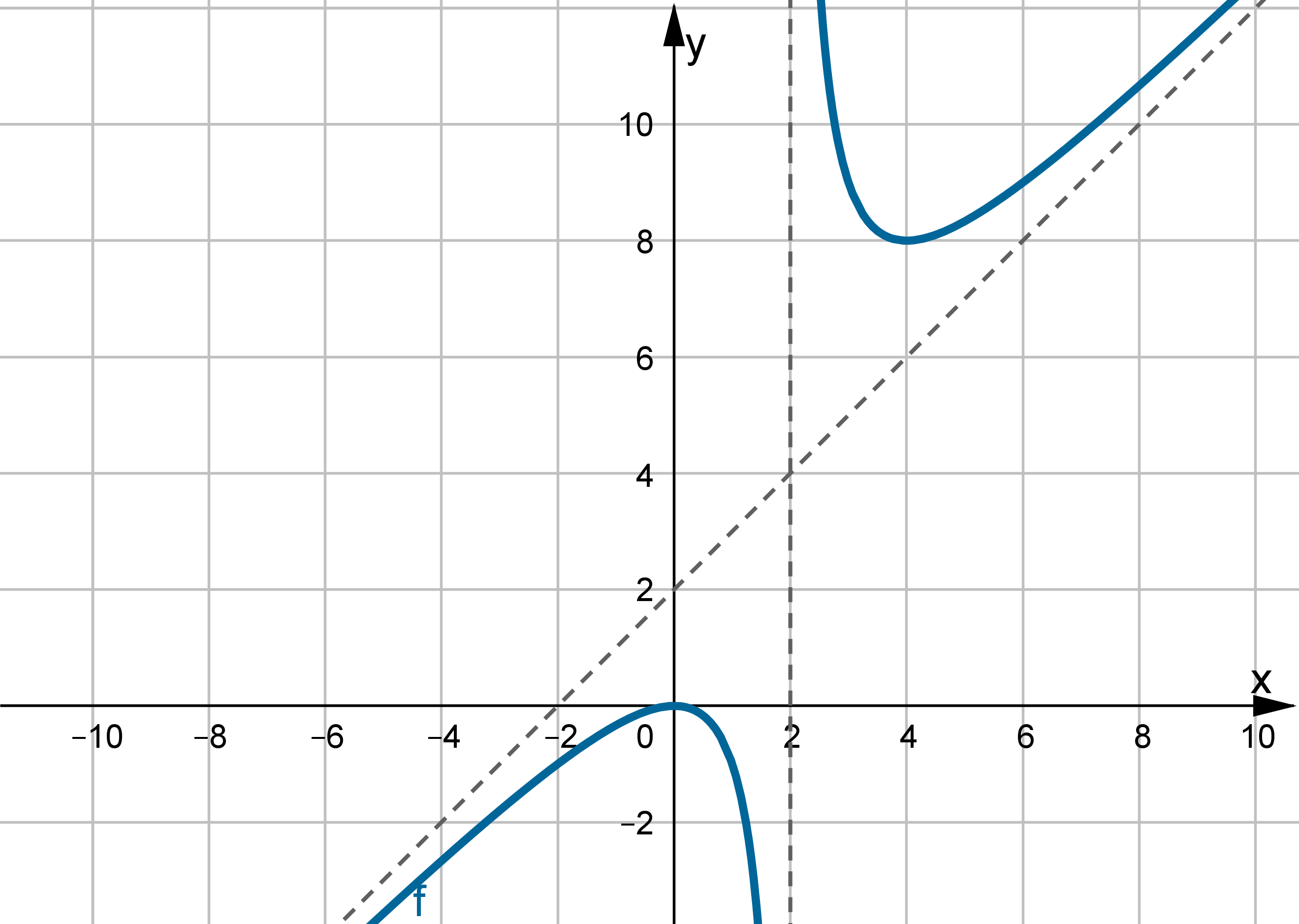
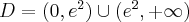 .
. 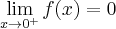 , wykres funkcji ma asymptotę pionową obustronną
, wykres funkcji ma asymptotę pionową obustronną 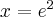 ,
, 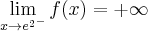 ,
, 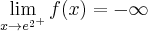 ,
, 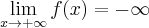 , brak asymptoty ukośnej. Funkcja jest rosnąca na każdym z przedziałów:
, brak asymptoty ukośnej. Funkcja jest rosnąca na każdym z przedziałów: 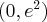 ,
, 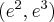 , malejąca na przedziale
, malejąca na przedziale 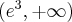 , w punkcie
, w punkcie 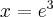 funkcja ma maksimum lokalne równe
funkcja ma maksimum lokalne równe  . Funkcja jest wypukła na każdym z przedziałów
. Funkcja jest wypukła na każdym z przedziałów 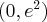 ,
, 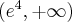 , wklęsła na przedziale
, wklęsła na przedziale 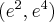 , punkt
, punkt 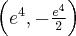 jest punktem przegięcia wykresu funkcji.
jest punktem przegięcia wykresu funkcji.
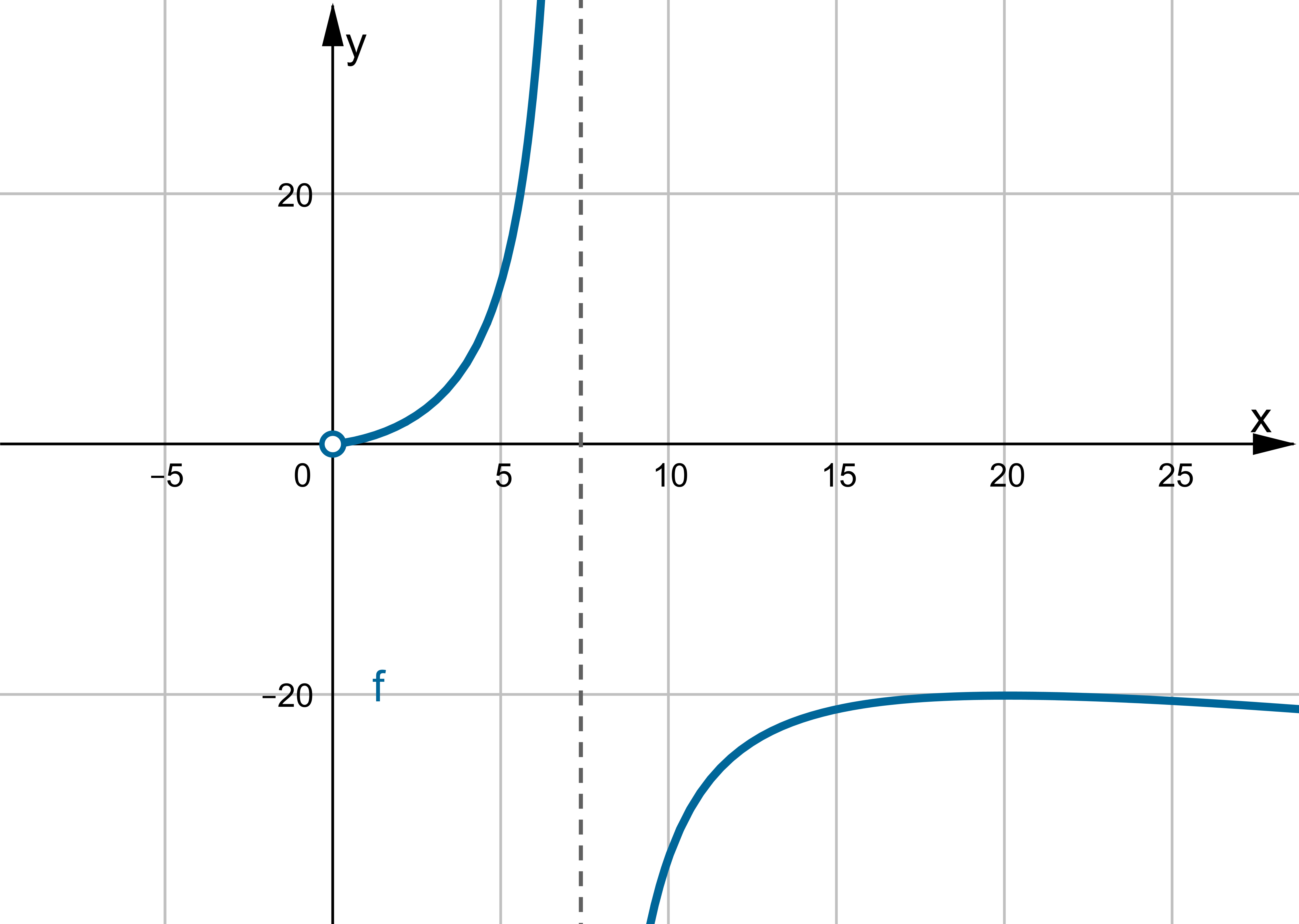
 . Wykres funkcji ma asymptotę pionową prawostronną
. Wykres funkcji ma asymptotę pionową prawostronną 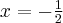 ,
, 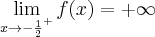 ,
, 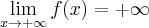 , brak asymptoty ukośnej. Funkcja jest malejąca na przedziale
, brak asymptoty ukośnej. Funkcja jest malejąca na przedziale 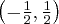 , rosnąca na przedziale
, rosnąca na przedziale 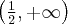 , w punkcie
, w punkcie  funkcja ma minimum lokalne równe
funkcja ma minimum lokalne równe 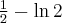 . Funkcja jest wypukła w całej dziedzinie.
. Funkcja jest wypukła w całej dziedzinie.

 .
. 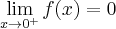 ,
, 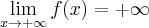 , brak asymptot. Funkcja jest malejąca na przedziale
, brak asymptot. Funkcja jest malejąca na przedziale 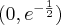 , rosnąca na przedziale
, rosnąca na przedziale  , w punkcie
, w punkcie 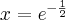 funkcja ma minimum lokalne równe
funkcja ma minimum lokalne równe 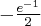 . Funkcja jest wypukła na przedziale:
. Funkcja jest wypukła na przedziale: 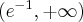 , wklęsła na przedziale
, wklęsła na przedziale 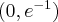 , punkt
, punkt 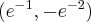 jest punktem przegięcia wykresu funkcji.
jest punktem przegięcia wykresu funkcji.
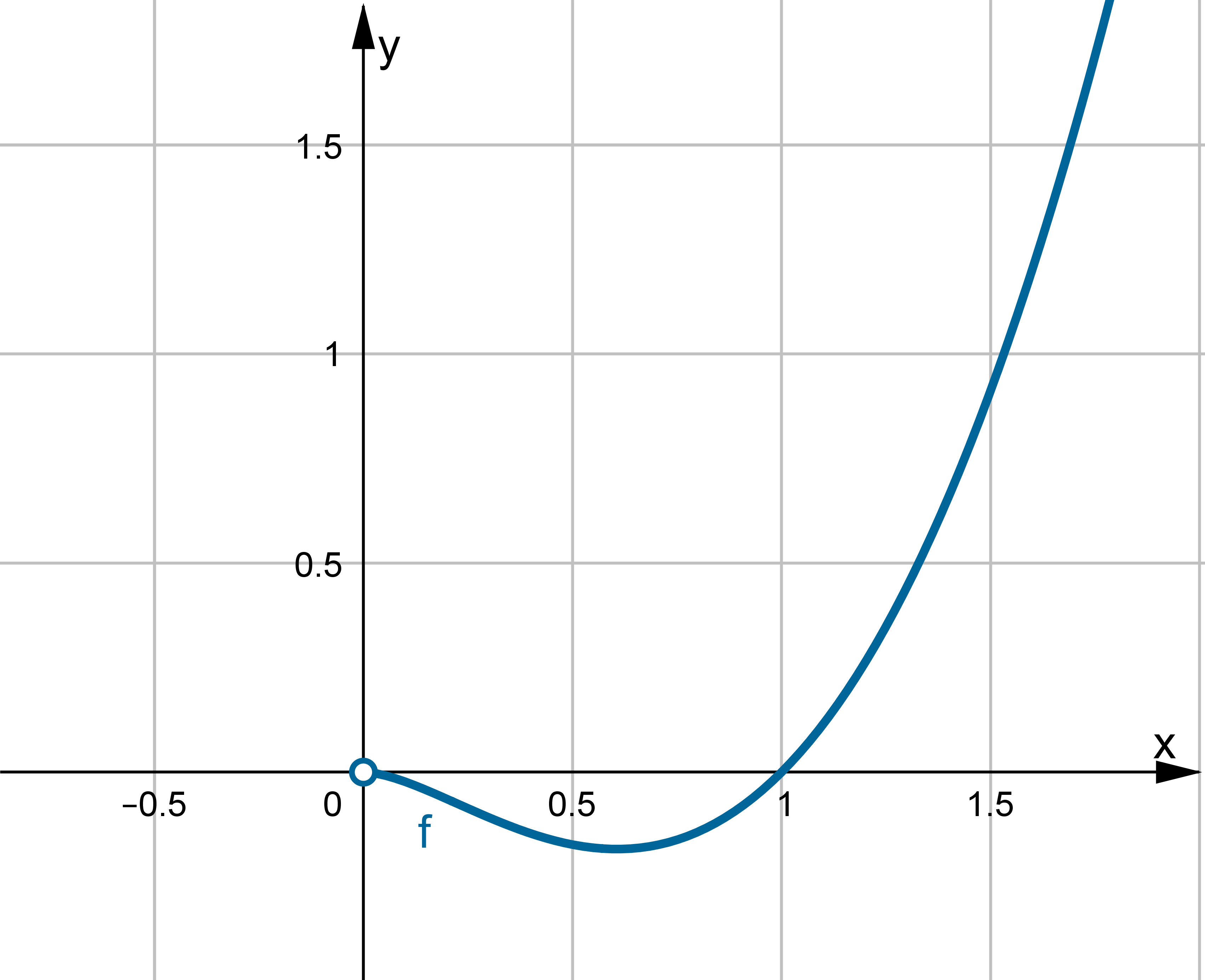
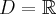 . Wykres funkcji ma asymptotę poziomą
. Wykres funkcji ma asymptotę poziomą 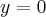 w
w 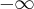 ,
, 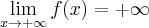 . Funkcja jest malejąca na przedziale
. Funkcja jest malejąca na przedziale  , rosnąca na każdym z przedziałów
, rosnąca na każdym z przedziałów 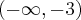 ,
, 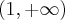 , w punkcie
, w punkcie 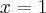 funkcja ma minimum lokalne równe
funkcja ma minimum lokalne równe  , w punkcie
, w punkcie  funkcja ma maksimum lokalne równe
funkcja ma maksimum lokalne równe  . Funkcja jest wypukła na każdym z przedziałów:
. Funkcja jest wypukła na każdym z przedziałów: 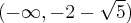 ,
,  , wklęsła na przedziale
, wklęsła na przedziale  , punkty
, punkty 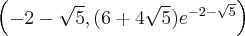 ,
,  są punktami przegięcia wykresu funkcji.
są punktami przegięcia wykresu funkcji.
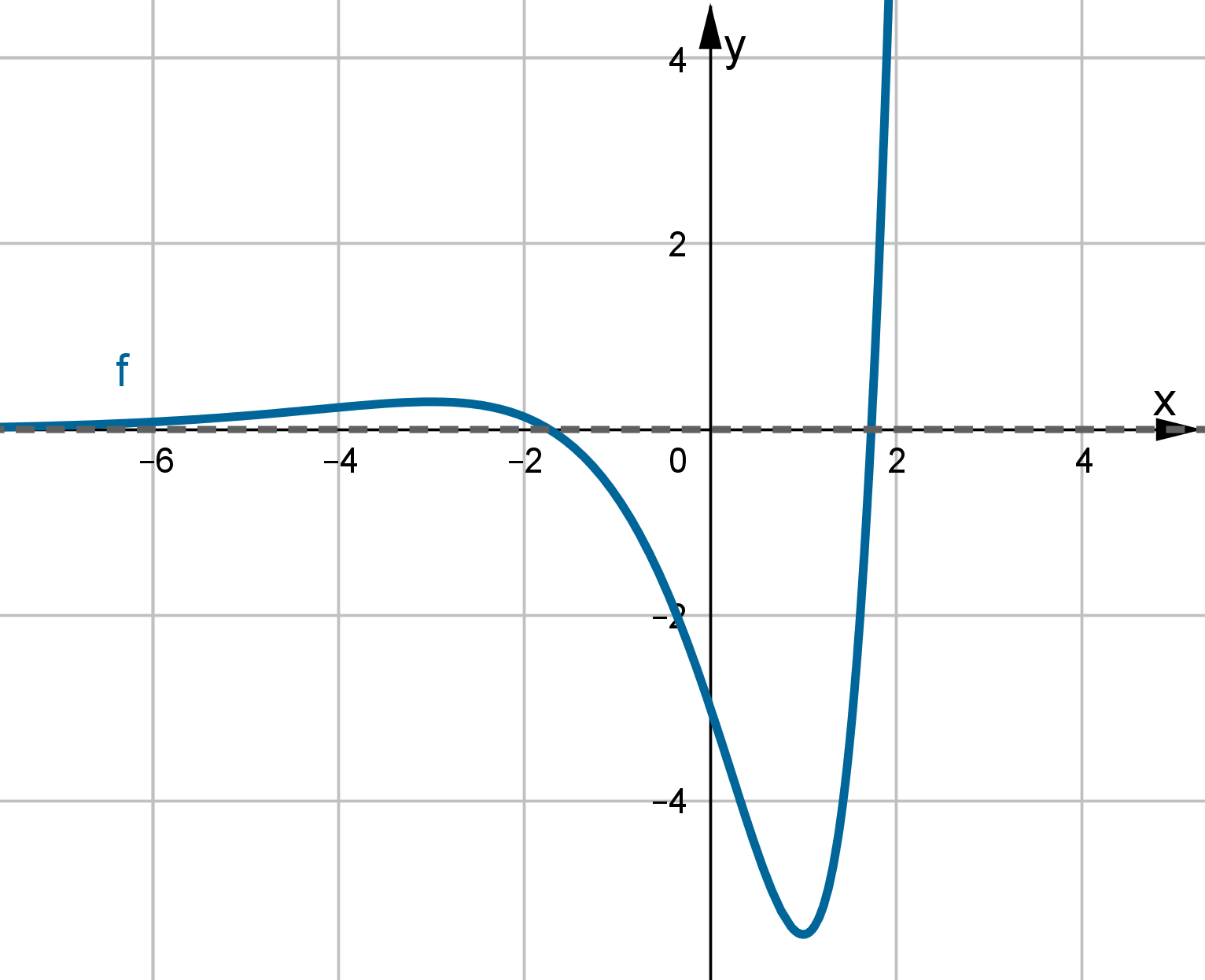
7. Pochodna w zastosowaniach praktycznych - przykłady
Od podwojonej pewnej liczby ujemnej odjęto kwadrat jej odwrotności. Jaka powinna być ta liczba, aby wartość tak otrzymanego wyrażenia była największa?
Oznaczmy przez  szukaną liczbę. Wówczas funkcja opisująca warunki zadania ma postać:
szukaną liczbę. Wówczas funkcja opisująca warunki zadania ma postać:
Wyznaczamy punkty stacjonarne funkcji  :
:
Rozwiązujemy odpowiednie nierówności pamiętając, że  :
:
Z I warunku wystarczającego istnienia ekstremum lokalnego wynika, że funkcja  ma maksimum lokalne dla
ma maksimum lokalne dla  . Czyli szukaną liczbą jest
. Czyli szukaną liczbą jest  .
.
Pewien tokarz otrzymał mosiężną kulę o promieniu  by wykonać z niej walec o jak największej objętości. Jakie będą wymiary tego walca i jaka będzie objętość skrawków?
by wykonać z niej walec o jak największej objętości. Jakie będą wymiary tego walca i jaka będzie objętość skrawków?
Niech  oznacza promień podstawy walca wpisanego w kulę, zaś
oznacza promień podstawy walca wpisanego w kulę, zaś  jego wysokość. Wykonujemy pomocniczy rysunek (aplet), na którym możemy zaobserwować, w jaki sposób objętość walca zależy od jego wysokości:
jego wysokość. Wykonujemy pomocniczy rysunek (aplet), na którym możemy zaobserwować, w jaki sposób objętość walca zależy od jego wysokości:
Przypomnijmy wzór na objętość walca
Z twierdzenia Pitagorasa (zastosowanego do trójkąta prostokątnego będącego połową przekroju osiowego walca) wynika, że
Stąd  . Wstawiając do wzoru na objętość walca otrzymujemy:
. Wstawiając do wzoru na objętość walca otrzymujemy:
Dalej wyznaczymy największą wartość funkcji  . W tym celu obliczamy pochodną
. W tym celu obliczamy pochodną
i przyrównujemy ją do zera:
 dla
dla  , natomiast
, natomiast  dla
dla  . A zatem walec przyjmuje największą objętość dla
. A zatem walec przyjmuje największą objętość dla  cm i objętość ta jest równa
cm i objętość ta jest równa
Pozostaje obliczyć jeszcze objętość kuli
i na koniec objętość skrawków
Dana jest funkcja ![f(x)=\frac12(x+3)\sqrt{2-x},\;\; x\in [-2,2] f(x)=\frac12(x+3)\sqrt{2-x},\;\; x\in [-2,2]](https://port.edu.p.lodz.pl/filter/tex/pix.php/b08973d0afd694288627df52f04ec353.png) . Wyznacz taki punkt na wykresie funkcji
. Wyznacz taki punkt na wykresie funkcji  , którego odległość od punktu
, którego odległość od punktu  jest najmniejsza.
jest najmniejsza.
Niech ![P=(x,f(x)), \;x\in [-2,2] P=(x,f(x)), \;x\in [-2,2]](https://port.edu.p.lodz.pl/filter/tex/pix.php/229ff2b9b24066c4212d1f1f5204f0d5.png) będzie punktem wykresu funkcji
będzie punktem wykresu funkcji  . Wówczas odległość
. Wówczas odległość  tego punktu od początku układu współrzędnych można przedstawić jako funkcję zmiennej
tego punktu od początku układu współrzędnych można przedstawić jako funkcję zmiennej 
Po podstawieniu otrzymujemy
Obliczamy najpierw pochodną funkcji 
i przyrównujemy ją do zera:
Zgodnie z algorytmem wyznaczania ekstremów globalnych funkcja  może posiadać minimum globalne w punktach:
może posiadać minimum globalne w punktach:  oraz
oraz  . Obliczamy wartości funkcji we wskazanych punktach:
. Obliczamy wartości funkcji we wskazanych punktach:
Stąd wynika, że funkcja  przyjmuje wartość najmniejszą na przedziale
przyjmuje wartość najmniejszą na przedziale ![[-2,2] [-2,2]](https://port.edu.p.lodz.pl/filter/tex/pix.php/98fab4cc523eb62bb9cf3a4fbefb7a69.png) w punktach
w punktach  oraz
oraz  . Punkty wykresu funkcji
. Punkty wykresu funkcji  , których odległość od początku układu jest najmniejsza to
, których odległość od początku układu jest najmniejsza to  oraz
oraz  . Odległość ta wynosi
. Odległość ta wynosi  .
.
Poniższy aplet przedstawia wykres funkcji  z ruchomym punktem
z ruchomym punktem  oraz funkcję
oraz funkcję  .
.
Dwa miasta  i
i  położone po przeciwnych stronach rzeki trzeba połączyć drogą z mostem prostopadłym do brzegów rzeki o prostoliniowych i równoległych brzegach. W którym miejscu należy wybudować most, aby droga łącząca te miasta miała najmniejszą długość? Odległość miasta
położone po przeciwnych stronach rzeki trzeba połączyć drogą z mostem prostopadłym do brzegów rzeki o prostoliniowych i równoległych brzegach. W którym miejscu należy wybudować most, aby droga łącząca te miasta miała najmniejszą długość? Odległość miasta  od rzeki wynosi
od rzeki wynosi  km, odległość miasta
km, odległość miasta  od rzeki wynosi
od rzeki wynosi  km, zaś odległość między rzutami miast na linię rzeki to
km, zaś odległość między rzutami miast na linię rzeki to  km.
km.

Niech  będzie odległością mostu od rzutu miasta
będzie odległością mostu od rzutu miasta  na linię rzeki. Wówczas
na linię rzeki. Wówczas  , zaś droga łącząca miasta
, zaś droga łącząca miasta  i
i  ma długość
ma długość
Ponieważ odcinek  równy długości mostu ma stałą długość, wystarczy, że znajdziemy najmniejszą wartość funkcji
równy długości mostu ma stałą długość, wystarczy, że znajdziemy najmniejszą wartość funkcji  na przedziale
na przedziale ![[0,21] [0,21]](https://port.edu.p.lodz.pl/filter/tex/pix.php/faa027f55788c0be58d3fa3d24c10ae1.png) .
.
i przyrównujemy ją do zera:
Ponieważ
więc
Zgodnie z algorytmem wyznaczania ekstremów globalnych funkcja  może posiadać minimum globalne w punktach:
może posiadać minimum globalne w punktach:  oraz
oraz  . Obliczamy wartości funkcji we wskazanych punktach:
. Obliczamy wartości funkcji we wskazanych punktach:
Stąd wynika, że funkcja  przyjmuje wartość najmniejszą na przedziale
przyjmuje wartość najmniejszą na przedziale ![[0,21] [0,21]](https://port.edu.p.lodz.pl/filter/tex/pix.php/faa027f55788c0be58d3fa3d24c10ae1.png) w punkcie
w punkcie  . Most należy zatem wybudować w odległości
. Most należy zatem wybudować w odległości  km od miasta
km od miasta  (licząc wzdłuż brzegu rzeki).
(licząc wzdłuż brzegu rzeki).
Stacja orbitalna porusza się prostoliniowo na wysokości  km nad Ziemią z prędkością
km nad Ziemią z prędkością  km/h. Antena odbierająca sygnały znajduje się bezpośrednio pod trajektorią stacji. W każdej chwili oś anteny jest skierowana na stację. Jaka jest prędkość kątowa anteny w chwili, gdy stacja znajduje się w odległości
km/h. Antena odbierająca sygnały znajduje się bezpośrednio pod trajektorią stacji. W każdej chwili oś anteny jest skierowana na stację. Jaka jest prędkość kątowa anteny w chwili, gdy stacja znajduje się w odległości  km od anteny?
km od anteny?
Stół bilardowy ma następujący kształt (bandy są w kształcie parabol). Gracz ma możliwość ustawienia bili w dowolnym miejscu na linii łączącej wierzchołki parabol. Jego zadanie polega na trafieniu do pokazanego otworu przy wykorzystaniu dokładnie jednego odbicia od bandy. Zakładając, że ustawił bilę w konkretnym miejscu, w którym kierunku powinien uderzyć?
Obróćmy stół bilardowy i opiszmy go funkcjami następująco:

Rozważymy jedną przykładową sytuację. Czytelnik może przeanalizować każdy inny przypadek samodzielnie. Załóżmy zatem, że otwór na stole bilardowym znajduje się w miejscu:  Z prawa odbicia wynika, że bila (która leży na części osi
Z prawa odbicia wynika, że bila (która leży na części osi  zawartej pomiędzy parabolami) pchnięta w stronę ramienia paraboli, odbije się od niej pod kątem równym kątowi padania na to ramię, czyli
zawartej pomiędzy parabolami) pchnięta w stronę ramienia paraboli, odbije się od niej pod kątem równym kątowi padania na to ramię, czyli

będzie poruszała się wzdłuż prostej padania i po odbiciu wróci wzdłuż prostej odbicia.
Prosta  jest styczną do paraboli w punkcie, w którym uderzy bila, prosta
jest styczną do paraboli w punkcie, w którym uderzy bila, prosta 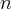 jest prostopadła do stycznej, kąty padania i odbicia pokazane są na rysunku.
jest prostopadła do stycznej, kąty padania i odbicia pokazane są na rysunku.
Zakładamy, że bilę umieścimy na stole bilardowym w punkcie 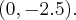
Wówczas należy uderzyć bilę w kierunku prostej o równaniu 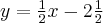 w kierunku lewej bandy (w przypadku uderzania w prawą bandę, prosta miałaby równanie
w kierunku lewej bandy (w przypadku uderzania w prawą bandę, prosta miałaby równanie 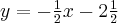 ).
).
Bila odbije się od bandy w punkcie 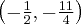 .
.
Styczna do bandy w tym punkcie ma równanie 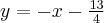 , zaś prosta odbicia
, zaś prosta odbicia 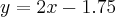 .
.
Bila, po odbicu, potoczy się do wskazanego otworu.
Koszt całkowity produkcji zależny od wielkości produkcji określa funkcja: 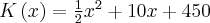 .
.
(a) Wyznaczymy koszt krańcowy dla pewnych wielkości produkcji.
(b) Sprawdzimy, kiedy producent zrealizuje maksymalny zysk (optimum ekonomiczne) przy określonej cenie sprzedaży jednostki produktu.
(c) Ustalimy wielkość produkcji zapewniającą minimalny koszt jednostkowy (optimum techniczne).
(a) Koszt krańcowy produkcji jest równy pochodnej funkcji  :
:
Dla wielkości produkcji 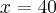 ,
, 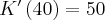 , zaś dla
, zaś dla 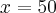 ,
, 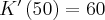 . Oznacza to, że wytworzenie dodatkowej jednostki produktu przy wielkości produkcji
. Oznacza to, że wytworzenie dodatkowej jednostki produktu przy wielkości produkcji  jednostek wynosi
jednostek wynosi  jednostek pieniężnych, a przy wielkości produkcji
jednostek pieniężnych, a przy wielkości produkcji  jednostek wynosi więcej, bo
jednostek wynosi więcej, bo  jednostek pieniężnych.
jednostek pieniężnych.
(b) Zakładamy, że cała produkcja może zostać sprzedana. Załóżmy teraz , że cena sprzedaży jednostki produktu wynosi 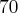 j.p. Niech funkcja
j.p. Niech funkcja 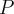 oznacza przychód ze sprzedaży,
oznacza przychód ze sprzedaży, 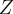 - zysk producenta. Wtedy:
- zysk producenta. Wtedy: 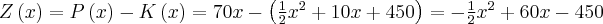 .
. 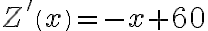 ,
, 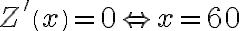 . Ponadto
. Ponadto 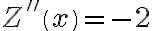 . Oznacza to, że przy wielkości produkcji
. Oznacza to, że przy wielkości produkcji 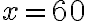 jednostek producent osiągnie maksymalny zysk w wysokości
jednostek producent osiągnie maksymalny zysk w wysokości 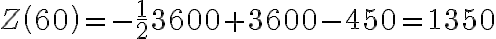 , czyli
, czyli  j.p. (c) Niech funkcja
j.p. (c) Niech funkcja  oznacza koszt jednostkowy.
oznacza koszt jednostkowy. 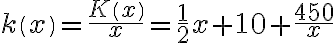 .
. 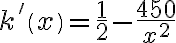 . Stąd
. Stąd 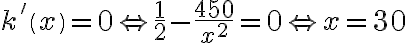 . Ponadto
. Ponadto 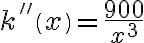 i
i 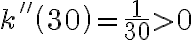 . Tym samym przy produkcji
. Tym samym przy produkcji 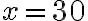 j.p. koszt jednostkowy jest minimalny i wynosi
j.p. koszt jednostkowy jest minimalny i wynosi 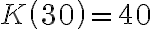 j.p.
j.p.



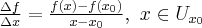






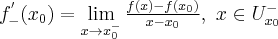

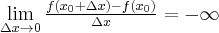

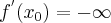


































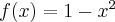
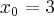
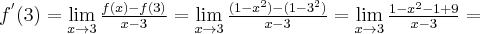
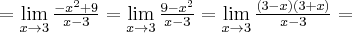
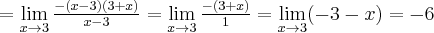
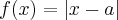
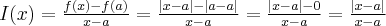
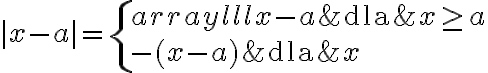
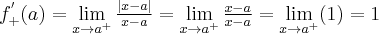
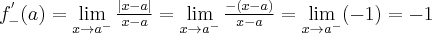
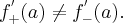

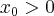
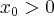
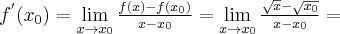
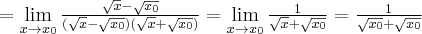
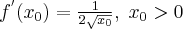
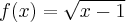
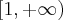
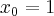
![f_{+}^{^{\prime }}(1)=\lim\limits_{x\rightarrow 1^{+}}\frac{f(x)-f(1)}{x-1} =\lim\limits_{x\rightarrow 1^{+}}\frac{\sqrt{x-1}-\sqrt{1-1}}{x-1}= \lim\limits_{x\rightarrow 1^{+}}\frac{\sqrt{x-1}}{x-1}=\lim\limits_{x \rightarrow 1^{+}}\frac{1}{\sqrt{x-1}}=\left[\frac{1}{0^{+}}\right]=+\infty . f_{+}^{^{\prime }}(1)=\lim\limits_{x\rightarrow 1^{+}}\frac{f(x)-f(1)}{x-1} =\lim\limits_{x\rightarrow 1^{+}}\frac{\sqrt{x-1}-\sqrt{1-1}}{x-1}= \lim\limits_{x\rightarrow 1^{+}}\frac{\sqrt{x-1}}{x-1}=\lim\limits_{x \rightarrow 1^{+}}\frac{1}{\sqrt{x-1}}=\left[\frac{1}{0^{+}}\right]=+\infty .](https://port.edu.p.lodz.pl/filter/tex/pix.php/bd5a2abdbcbe6c961b439381cc9cb17c.png)
![\sqrt[3]{1003} \sqrt[3]{1003}](https://port.edu.p.lodz.pl/filter/tex/pix.php/21198aaf21c8295ae62ce5956d6ee3e6.png)
![f(x)=\sqrt[3]{x} f(x)=\sqrt[3]{x}](https://port.edu.p.lodz.pl/filter/tex/pix.php/415c4f39a1a68ccac15da99969baacfc.png)
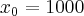
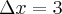
![f'(x)=\left(x^\frac{1}{3}\right)'=\frac{1}{3} x^{-\frac{2}{3}}=\frac{1}{3 \sqrt[3]{x^2}} f'(x)=\left(x^\frac{1}{3}\right)'=\frac{1}{3} x^{-\frac{2}{3}}=\frac{1}{3 \sqrt[3]{x^2}}](https://port.edu.p.lodz.pl/filter/tex/pix.php/4cd84df3cc7145002e071a84220a14c2.png)
![f'(x_0)=\frac{1}{3( \sqrt[3]{1000})^2}=\frac{1}{300} f'(x_0)=\frac{1}{3( \sqrt[3]{1000})^2}=\frac{1}{300}](https://port.edu.p.lodz.pl/filter/tex/pix.php/03f578dee63d18ee1d37e2921b032754.png)
![\sqrt[3]{1003}=f(1000+3)\approx f(1000)+f^\prime(1000)\cdot 3 = 10+\frac{1}{300}\cdot 3=10.01 \sqrt[3]{1003}=f(1000+3)\approx f(1000)+f^\prime(1000)\cdot 3 = 10+\frac{1}{300}\cdot 3=10.01](https://port.edu.p.lodz.pl/filter/tex/pix.php/e552baeea97fe6eaec5a60c8f5592568.png)
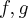
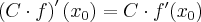
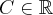
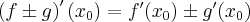
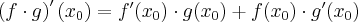
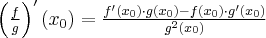
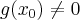
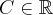
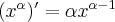
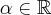
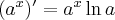
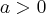
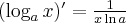
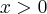
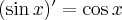
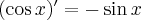
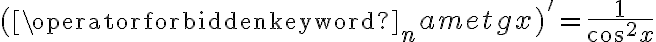
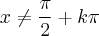
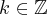
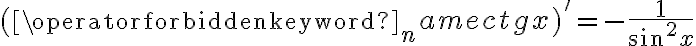
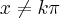
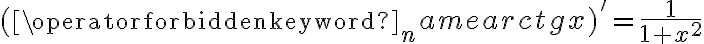
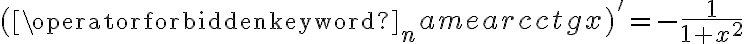
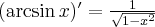
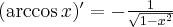
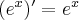
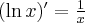
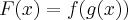

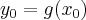
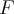
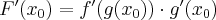
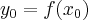
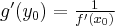
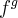
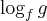
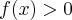

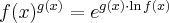
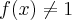
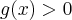
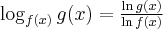
![f(x)=4x^5-3x^2+x\sqrt[3]x-\ln 3 f(x)=4x^5-3x^2+x\sqrt[3]x-\ln 3](https://port.edu.p.lodz.pl/filter/tex/pix.php/4c1597319373d765ab0bcec5bfa92402.png)
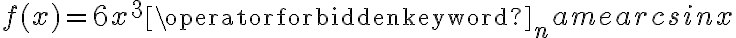
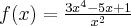
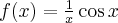

![f^\prime(x)=\left(4x^5-3x^2+x\sqrt[3]x-\ln 3\right)^\prime=4\left(x^5\right)^\prime-3\left(x^2\right)^\prime+\left(x^{\frac43}\right)^\prime-\left(\ln 3\right)^\prime= f^\prime(x)=\left(4x^5-3x^2+x\sqrt[3]x-\ln 3\right)^\prime=4\left(x^5\right)^\prime-3\left(x^2\right)^\prime+\left(x^{\frac43}\right)^\prime-\left(\ln 3\right)^\prime=](https://port.edu.p.lodz.pl/filter/tex/pix.php/514b051c428e523d73f06927e47beccc.png)
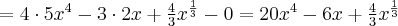
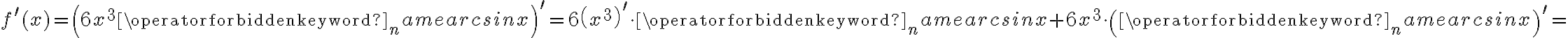
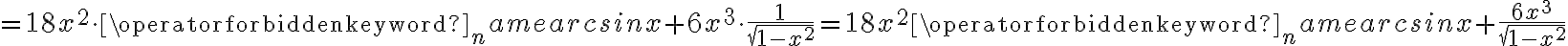
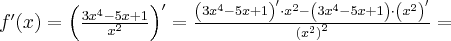
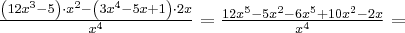
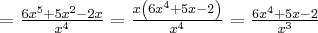
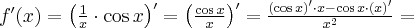
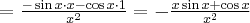
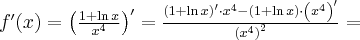
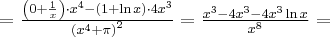
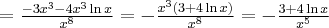
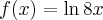
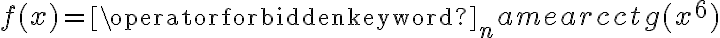
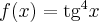
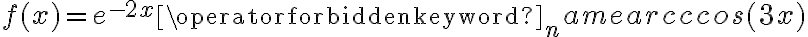
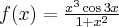
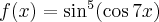
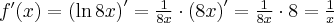
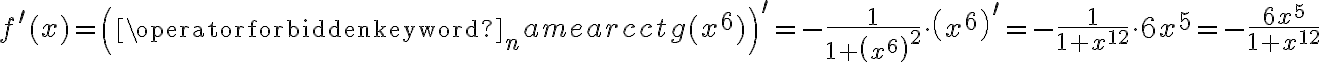
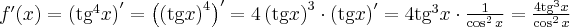
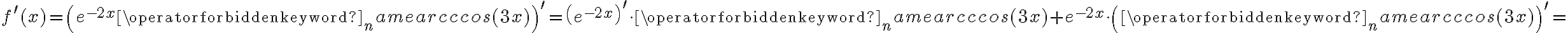
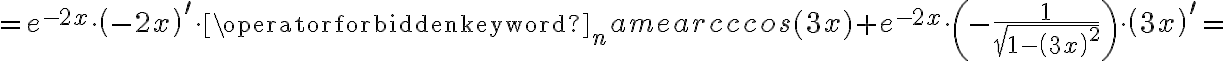
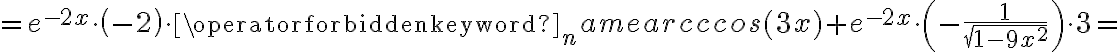
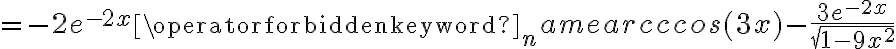
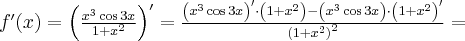
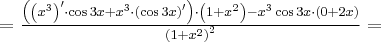
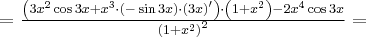
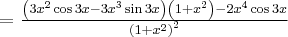
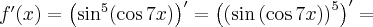
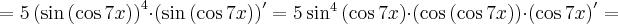
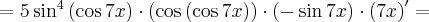
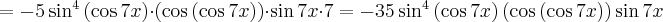
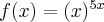
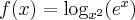
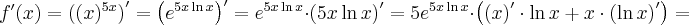
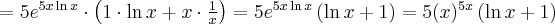
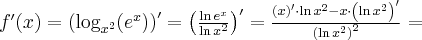
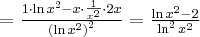
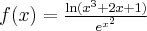
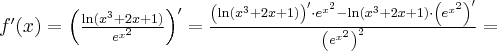
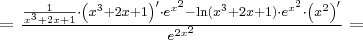
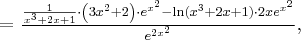
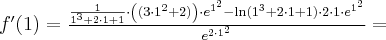
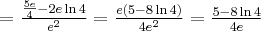







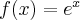

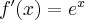
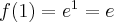
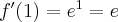
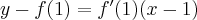
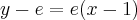
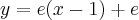
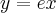
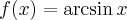
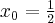
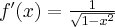

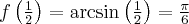
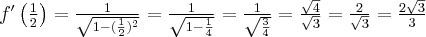
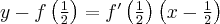
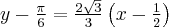
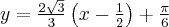
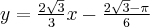

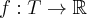


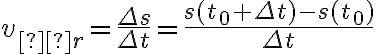
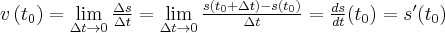
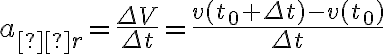
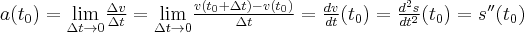
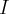
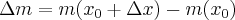
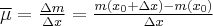
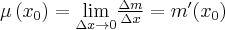







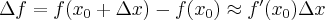










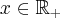












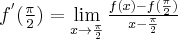








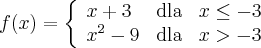





















![f(x)=2x^5+4e\sqrt[3]x+\frac1{x^6}-7 f(x)=2x^5+4e\sqrt[3]x+\frac1{x^6}-7](https://port.edu.p.lodz.pl/filter/tex/pix.php/138fc9c336cfff3ec499714eb4e63e45.png)









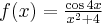

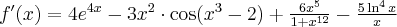




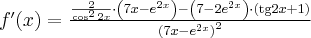


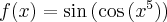
















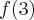


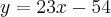



















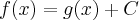
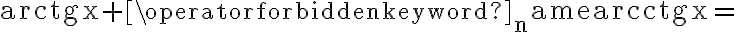
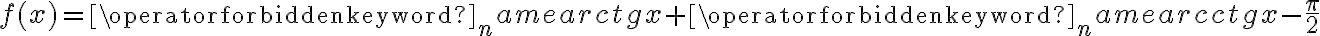
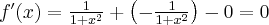
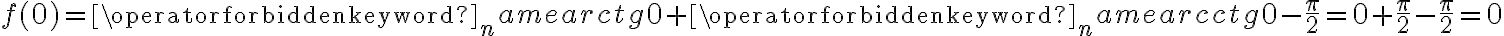
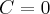
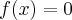
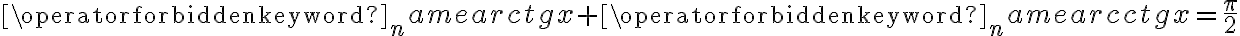
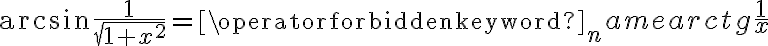

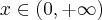

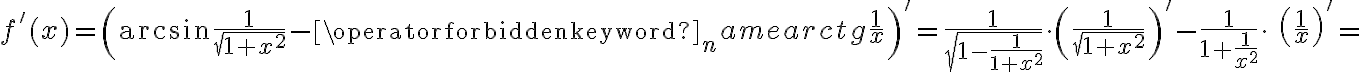
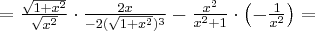
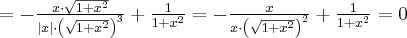
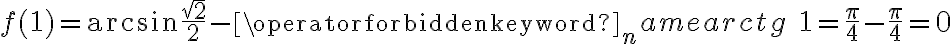
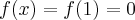
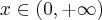
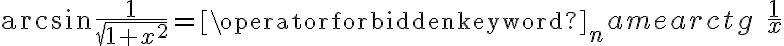
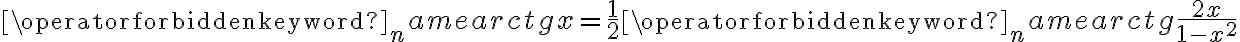
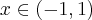
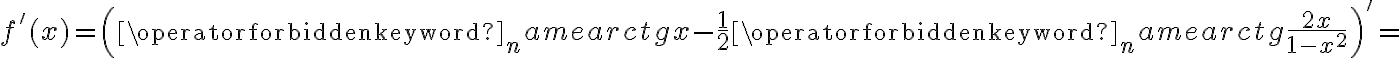
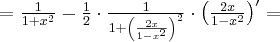
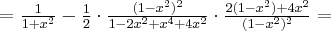
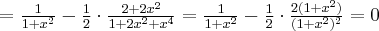
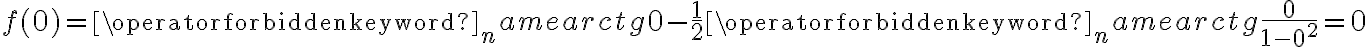
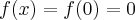
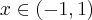
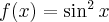
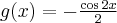
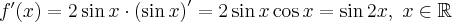
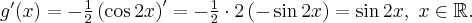
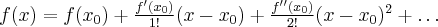
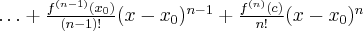
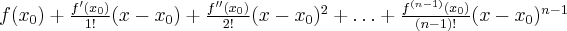
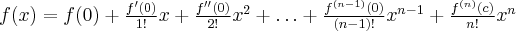
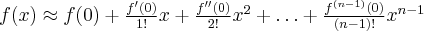
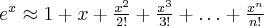
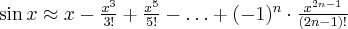
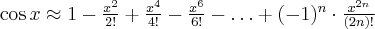
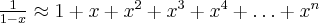
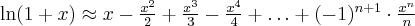
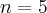
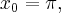
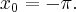
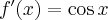
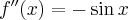
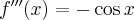
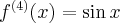
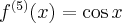
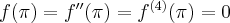
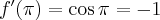
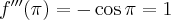
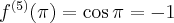
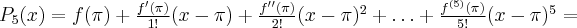
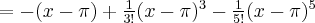
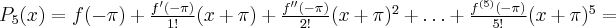
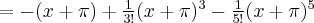
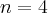
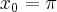
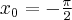
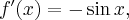
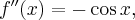
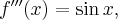
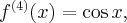
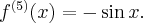
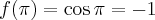
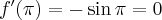
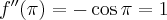
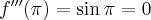
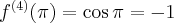
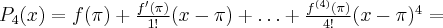
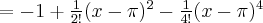
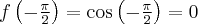
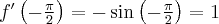
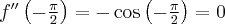
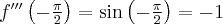
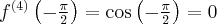
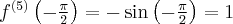
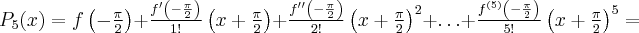
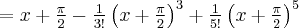
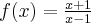
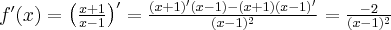
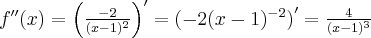
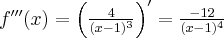
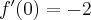
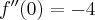
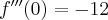
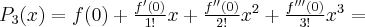
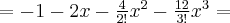
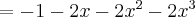
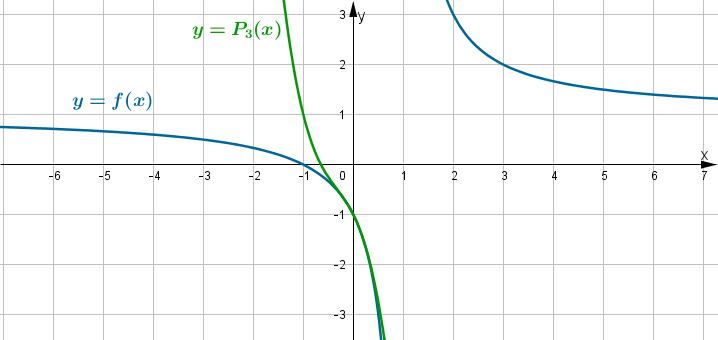
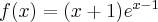
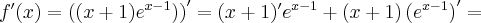
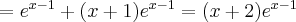
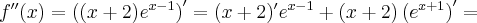
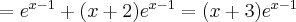
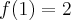
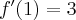
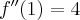
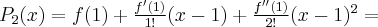
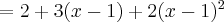
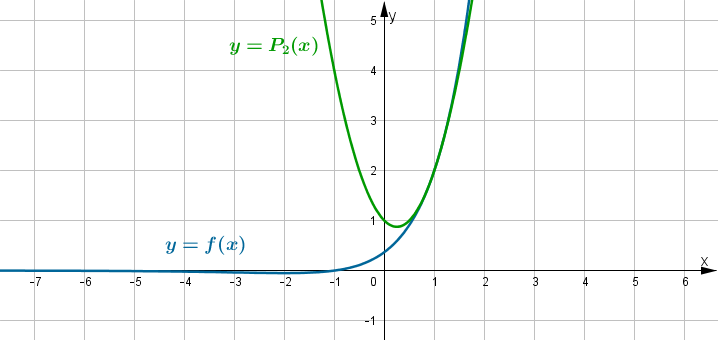
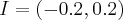
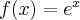
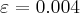
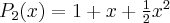
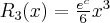
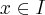
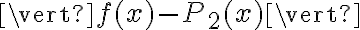
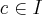
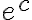
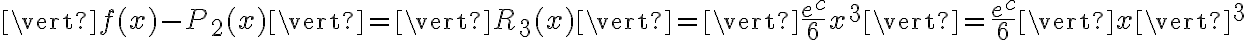
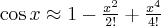
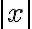
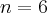
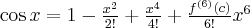
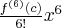
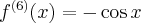
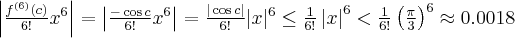








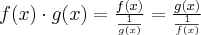

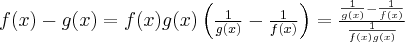









![\dfrac{e^x-1}{2\sin x} = \left[\dfrac{0}{0}\right] \dfrac{e^x-1}{2\sin x} = \left[\dfrac{0}{0}\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/3a32e8a400e82e6025c8fc27f796d3e7.png)



![\underset{x\rightarrow +\infty }{\lim }\, \dfrac{x}{\ln x} = \left[\dfrac{\infty}{\infty}\right] \overset{\text{H}}{=} \underset{x\rightarrow +\infty }{\lim }\, \dfrac{x}{\ln x} = \left[\dfrac{\infty}{\infty}\right] \overset{\text{H}}{=}](https://port.edu.p.lodz.pl/filter/tex/pix.php/f51b93dc00924ac3be8ae55eb4aec36b.png)

![\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\ln x }{x} = \left[\dfrac{-\infty}{0^{+}}\right]. \underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\ln x }{x} = \left[\dfrac{-\infty}{0^{+}}\right].](https://port.edu.p.lodz.pl/filter/tex/pix.php/d8ff9a271b17743a4c7cfd0f3a66f70e.png)
![\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\ln x }{x} = \underset{x\rightarrow 0^{+} }{\lim }\, \ln x \cdot \dfrac{1}{x} =\left[-\infty \cdot \dfrac{1}{0^{+}}\right] = [-\infty \cdot \infty]=-\infty. \underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\ln x }{x} = \underset{x\rightarrow 0^{+} }{\lim }\, \ln x \cdot \dfrac{1}{x} =\left[-\infty \cdot \dfrac{1}{0^{+}}\right] = [-\infty \cdot \infty]=-\infty.](https://port.edu.p.lodz.pl/filter/tex/pix.php/d9c9c4343188476654c6443e78e3ba90.png)
![\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{(\ln x)'}{(x)'} =\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\frac{1}{x}}{1} = \left[\dfrac{1}{0^{+}}\right] = +\infty \underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{(\ln x)'}{(x)'} =\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\frac{1}{x}}{1} = \left[\dfrac{1}{0^{+}}\right] = +\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/307501b572f59af6a574a7f2021ad6b8.png)



![\underset{x\rightarrow 0}{\lim }\,\dfrac{x\cos 2x}{x+\arcsin x} = \left[\dfrac{0}{0}\right]\overset{\text{H}}{=} \underset{x\rightarrow 0}{\lim }\dfrac{(x\cos 2x)'}{(x+\arcsin x)'}=\underset{x\rightarrow 0}{\lim }\,\dfrac{\cos 2x-x\sin 2x\cdot 2}{1+\frac{1}{\sqrt{1-x^{2}}}}= \underset{x\rightarrow 0}{\lim }\,\dfrac{x\cos 2x}{x+\arcsin x} = \left[\dfrac{0}{0}\right]\overset{\text{H}}{=} \underset{x\rightarrow 0}{\lim }\dfrac{(x\cos 2x)'}{(x+\arcsin x)'}=\underset{x\rightarrow 0}{\lim }\,\dfrac{\cos 2x-x\sin 2x\cdot 2}{1+\frac{1}{\sqrt{1-x^{2}}}}=](https://port.edu.p.lodz.pl/filter/tex/pix.php/10b4959c1038fb647798ed685676c5a1.png)
![\left[\dfrac{1-0}{1+1}\right]=\dfrac{1}{2}\, \left[\dfrac{1-0}{1+1}\right]=\dfrac{1}{2}\,](https://port.edu.p.lodz.pl/filter/tex/pix.php/25eb870e22a13f078b899d09b5c337ee.png)
![\underset{x\rightarrow + \infty }{\lim }\dfrac{e^{x^{2}}}{x^{3}}=\left[ \dfrac{\infty }{\infty }\right] \overset{\text{H}}{=}\underset{x\rightarrow +\infty } {\lim }\dfrac{(e^{x^{2}})^{\prime }}{(x^{3})^{\prime }}=\underset{ x\rightarrow +\infty }{\lim }\dfrac{e^{x^{2}}\cdot 2x}{3x^{2}}=\underset{ x\rightarrow +\infty }{\lim }\dfrac{2e^{x^{2}}}{3x}=\left[ \dfrac{\infty }{\infty }\right] \overset{\text{H}}{=} \underset{x\rightarrow + \infty }{\lim }\dfrac{e^{x^{2}}}{x^{3}}=\left[ \dfrac{\infty }{\infty }\right] \overset{\text{H}}{=}\underset{x\rightarrow +\infty } {\lim }\dfrac{(e^{x^{2}})^{\prime }}{(x^{3})^{\prime }}=\underset{ x\rightarrow +\infty }{\lim }\dfrac{e^{x^{2}}\cdot 2x}{3x^{2}}=\underset{ x\rightarrow +\infty }{\lim }\dfrac{2e^{x^{2}}}{3x}=\left[ \dfrac{\infty }{\infty }\right] \overset{\text{H}}{=}](https://port.edu.p.lodz.pl/filter/tex/pix.php/5b80619ac8676c4a800681bf3a57b9d2.png)
![=\underset{ x\rightarrow +\infty }{\lim }\dfrac{(2e^{x^{2}})^{\prime }}{(3x)^{\prime }}=\underset{x\rightarrow +\infty }{\lim }\dfrac{2e^{x^{2}}\cdot 2x}{3 }=\left[ \dfrac{\infty}{3} \right] =\infty =\underset{ x\rightarrow +\infty }{\lim }\dfrac{(2e^{x^{2}})^{\prime }}{(3x)^{\prime }}=\underset{x\rightarrow +\infty }{\lim }\dfrac{2e^{x^{2}}\cdot 2x}{3 }=\left[ \dfrac{\infty}{3} \right] =\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/8a4a774eb1bb0f943edb6037da6c6f85.png)
![\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{\ln (\sin x )}{\ln ^{2}{x}}=\left[ \dfrac{-\infty }{\infty }\right] \overset{\text{H}}{=}\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{\frac{1}{\sin x}\cdot \cos x}{2\ln x \cdot \frac{1}{x}}=\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{x}{\sin x} \cdot \dfrac{\cos x}{2\ln x}=\left[ 1\cdot\dfrac{1}{-\infty}\right] =0 \underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{\ln (\sin x )}{\ln ^{2}{x}}=\left[ \dfrac{-\infty }{\infty }\right] \overset{\text{H}}{=}\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{\frac{1}{\sin x}\cdot \cos x}{2\ln x \cdot \frac{1}{x}}=\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{x}{\sin x} \cdot \dfrac{\cos x}{2\ln x}=\left[ 1\cdot\dfrac{1}{-\infty}\right] =0](https://port.edu.p.lodz.pl/filter/tex/pix.php/d561fe251231a59d20bc3ef61fef5c00.png)


![\underset{x\rightarrow +\infty }{\lim }\, \dfrac{x-\sin x }{x} = \left[\dfrac{\infty}{\infty}\right] \underset{x\rightarrow +\infty }{\lim }\, \dfrac{x-\sin x }{x} = \left[\dfrac{\infty}{\infty}\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/f48f480c622a09984ee03134a12800bd.png)

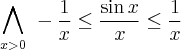
![\underset{x\rightarrow +\infty }{\lim }\dfrac{x-\sin x }{x}=\underset{x\rightarrow +\infty }{\lim }\left(1-\dfrac{\sin x}{x} \right)=[1-0]=1 \underset{x\rightarrow +\infty }{\lim }\dfrac{x-\sin x }{x}=\underset{x\rightarrow +\infty }{\lim }\left(1-\dfrac{\sin x}{x} \right)=[1-0]=1](https://port.edu.p.lodz.pl/filter/tex/pix.php/4c5f265f4283e60e82ecd5cf8dc4ff7a.png)
![\underset{x\rightarrow +\infty}{\lim }\,\dfrac{\sqrt{x^2+1}}{x}=\left[\dfrac{\infty}{\infty}\right]\overset{\text{H}}{=}\underset{x\rightarrow +\infty}{\lim }\,\dfrac{\frac{1}{2\sqrt{x^2+1}}\cdot 2x}{1}=\underset{x\rightarrow +\infty}{\lim }\,\dfrac{x}{\sqrt{x^2+1}}\overset{\text{H}}{=}\underset{x\rightarrow+ \infty}{\lim }\,\dfrac{\sqrt{x^2+1}}{x} \underset{x\rightarrow +\infty}{\lim }\,\dfrac{\sqrt{x^2+1}}{x}=\left[\dfrac{\infty}{\infty}\right]\overset{\text{H}}{=}\underset{x\rightarrow +\infty}{\lim }\,\dfrac{\frac{1}{2\sqrt{x^2+1}}\cdot 2x}{1}=\underset{x\rightarrow +\infty}{\lim }\,\dfrac{x}{\sqrt{x^2+1}}\overset{\text{H}}{=}\underset{x\rightarrow+ \infty}{\lim }\,\dfrac{\sqrt{x^2+1}}{x}](https://port.edu.p.lodz.pl/filter/tex/pix.php/4eae5571d7aa2578a16e83b947c34088.png)




![\lim\limits_{x\to + \infty }\,x^2 \,e^{-x}= \left[ \infty\cdot0 \,\right] \lim\limits_{x\to + \infty }\,x^2 \,e^{-x}= \left[ \infty\cdot0 \,\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/0516aaa46e442443d1fec0c616104686.png)
![\lim\limits_{x\to +\infty }\,x^2 \,e^{-x}=\lim\limits_{x\to +\infty } \dfrac{x^2}{e^x}=\left[ \dfrac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to +\infty } \dfrac{(x^2)'}{(e^x)'} = \lim\limits_{x\to +\infty }\,\dfrac{2x}{e^x} \lim\limits_{x\to +\infty }\,x^2 \,e^{-x}=\lim\limits_{x\to +\infty } \dfrac{x^2}{e^x}=\left[ \dfrac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to +\infty } \dfrac{(x^2)'}{(e^x)'} = \lim\limits_{x\to +\infty }\,\dfrac{2x}{e^x}](https://port.edu.p.lodz.pl/filter/tex/pix.php/7a87707e4486a2e482602f1fd1c8330e.png)
![=\left[ \dfrac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to +\infty }\,\dfrac{(2x)'}{(e^x)'} = \lim\limits_{x\to +\infty }\,\dfrac{2}{e^x} = \left[ \dfrac{2}{\infty} \right] = 0 =\left[ \dfrac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to +\infty }\,\dfrac{(2x)'}{(e^x)'} = \lim\limits_{x\to +\infty }\,\dfrac{2}{e^x} = \left[ \dfrac{2}{\infty} \right] = 0](https://port.edu.p.lodz.pl/filter/tex/pix.php/8568adb4c17df80de0f81c62d130d8ea.png)
![\lim\limits_{x\to 0^{+}}\,x \ln x=\left[ 0\cdot (-\infty) \right] \lim\limits_{x\to 0^{+}}\,x \ln x=\left[ 0\cdot (-\infty) \right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/135067031e61492d7de5429a2b9c1ee6.png)
![\lim\limits_{x\to 0^{+}} x\ln x=\lim\limits_{x\to 0^+}\dfrac{\ln x}{\frac{1}{x}}=\left[ \dfrac{-\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to 0^+}\dfrac{(\ln x)'}{(\frac{1}{x})'} \lim\limits_{x\to 0^{+}} x\ln x=\lim\limits_{x\to 0^+}\dfrac{\ln x}{\frac{1}{x}}=\left[ \dfrac{-\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to 0^+}\dfrac{(\ln x)'}{(\frac{1}{x})'}](https://port.edu.p.lodz.pl/filter/tex/pix.php/7aa38f9e30534a256c15a186be3e5035.png)


![\lim\limits_{x\to 0^{+} }x^x=\left[ 0^0\right] \lim\limits_{x\to 0^{+} }x^x=\left[ 0^0\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/abd653623333c1342282ffac79945643.png)

![\displaystyle \lim\limits_{x\to 0^{+} }x^x=\lim\limits_{x\to 0^{+} }e^{x\ln x}=\left[ e^0 \right]=1 \displaystyle \lim\limits_{x\to 0^{+} }x^x=\lim\limits_{x\to 0^{+} }e^{x\ln x}=\left[ e^0 \right]=1](https://port.edu.p.lodz.pl/filter/tex/pix.php/e0bdf2feebca2cc6a672b588f7b79179.png)


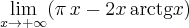
![\lim\limits_{x\to+ \infty } (e^{x^2}-x^3)=\left[\infty-\infty\right] =\lim\limits_{x\to +\infty } e^{x^2}\left(1-\dfrac{x^3}{e^{x^2}}\right) \lim\limits_{x\to+ \infty } (e^{x^2}-x^3)=\left[\infty-\infty\right] =\lim\limits_{x\to +\infty } e^{x^2}\left(1-\dfrac{x^3}{e^{x^2}}\right)](https://port.edu.p.lodz.pl/filter/tex/pix.php/2edce056c38c4224c25761738706ec2b.png)
![\lim\limits_{x\to+ \infty }\dfrac{x^3}{e^{x^2}}=\left[ \dfrac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to+ \infty } \dfrac{(x^3)'}{(e^{x^2})'} = \lim\limits_{x\to +\infty }\,\dfrac{3x^2}{2x\,e^{x^2}} = \lim\limits_{x\to +\infty }\,\dfrac{3x}{2\,e^{x^2}} \lim\limits_{x\to+ \infty }\dfrac{x^3}{e^{x^2}}=\left[ \dfrac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to+ \infty } \dfrac{(x^3)'}{(e^{x^2})'} = \lim\limits_{x\to +\infty }\,\dfrac{3x^2}{2x\,e^{x^2}} = \lim\limits_{x\to +\infty }\,\dfrac{3x}{2\,e^{x^2}}](https://port.edu.p.lodz.pl/filter/tex/pix.php/92411a055f061f6f408303086c95e284.png)
![= \left[ \dfrac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to +\infty }\,\dfrac{(3x)'}{(2e^{x^2})'} = \lim\limits_{x\to+ \infty }\,\dfrac{3}{4x\,e^{x^2}} = \left[ \dfrac{3}{\infty} \right] = 0 = \left[ \dfrac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to +\infty }\,\dfrac{(3x)'}{(2e^{x^2})'} = \lim\limits_{x\to+ \infty }\,\dfrac{3}{4x\,e^{x^2}} = \left[ \dfrac{3}{\infty} \right] = 0](https://port.edu.p.lodz.pl/filter/tex/pix.php/6d510f636f7469e87cfe2c0a7be30fe0.png)
![\lim\limits_{x\to+ \infty } e^{x^2}(1-\frac{x^3}{e^{x^2}})=\left[ \infty \cdot(1-0) \right]=\infty \lim\limits_{x\to+ \infty } e^{x^2}(1-\frac{x^3}{e^{x^2}})=\left[ \infty \cdot(1-0) \right]=\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/0d95713a31528a1b492e9b704cf372dd.png)
![\lim\limits_{x\to 0^{+} }\left( \dfrac1x-\dfrac{1}{\sin x}\right) = \left[\infty-\infty\right] \lim\limits_{x\to 0^{+} }\left( \dfrac1x-\dfrac{1}{\sin x}\right) = \left[\infty-\infty\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/5f26034f064d8d5c466b7ed92700d9d8.png)
![\lim\limits_{x\to 0^{+} }\left( \dfrac1x-\dfrac{1}{\sin x}\right) = \lim\limits_{x\to 0^{+} }\dfrac{\sin x-x}{x\sin x}= \left[ \dfrac{0}{0} \right] \overset{\text{H}}{=} \lim\limits_{x\to 0^{+} }\dfrac{(\sin x-x)'}{(x\sin x)'} \lim\limits_{x\to 0^{+} }\left( \dfrac1x-\dfrac{1}{\sin x}\right) = \lim\limits_{x\to 0^{+} }\dfrac{\sin x-x}{x\sin x}= \left[ \dfrac{0}{0} \right] \overset{\text{H}}{=} \lim\limits_{x\to 0^{+} }\dfrac{(\sin x-x)'}{(x\sin x)'}](https://port.edu.p.lodz.pl/filter/tex/pix.php/1f40b9f8f00d5187cf676e7f63e0466b.png)
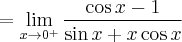
![= \left[ \dfrac{0}{0} \right]\overset{\text{H}}{=} \lim\limits_{x\to 0^{+} }\dfrac{-\sin x}{\cos x+\cos x-x\sin x}= \left[ \dfrac{0}{2} \right]=0 = \left[ \dfrac{0}{0} \right]\overset{\text{H}}{=} \lim\limits_{x\to 0^{+} }\dfrac{-\sin x}{\cos x+\cos x-x\sin x}= \left[ \dfrac{0}{2} \right]=0](https://port.edu.p.lodz.pl/filter/tex/pix.php/c3cb9ea4224a3a4222c2267240aaffab.png)
![\lim\limits_{x\to +\infty }(\pi\, x-2x\,\text{arctg} x)=\left[\infty-\infty\right] = \lim\limits_{x\to +\infty }x\,(\pi\,-2\,\text{arctg} x)=\left[ \infty\cdot 0\right] \lim\limits_{x\to +\infty }(\pi\, x-2x\,\text{arctg} x)=\left[\infty-\infty\right] = \lim\limits_{x\to +\infty }x\,(\pi\,-2\,\text{arctg} x)=\left[ \infty\cdot 0\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/f8c06a25e94b80f9e4e415d8f906a8a4.png)
![= \lim\limits_{x\to+ \infty }\dfrac{\pi\,-2\,\text{arctg} x}{\frac1x}= \left[ \dfrac{0}{0} \right] \overset{\text{H}}{=} \lim\limits_{x\to+\infty }\dfrac{(\pi\,-2\,\text{arctg} x)'}{(\frac1x)'} = \lim\limits_{x\to+ \infty }\dfrac{\pi\,-2\,\text{arctg} x}{\frac1x}= \left[ \dfrac{0}{0} \right] \overset{\text{H}}{=} \lim\limits_{x\to+\infty }\dfrac{(\pi\,-2\,\text{arctg} x)'}{(\frac1x)'}](https://port.edu.p.lodz.pl/filter/tex/pix.php/7dcb0b4aba4c455a35f6e03efb894949.png)





















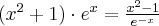







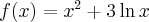
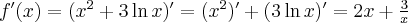
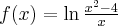
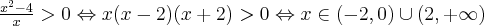
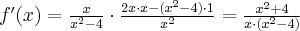
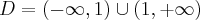
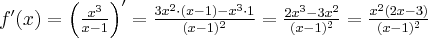
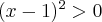
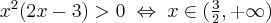
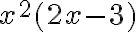
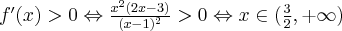
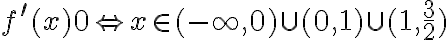
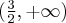
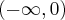
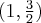
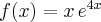
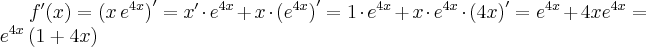
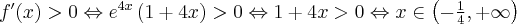
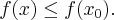







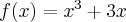
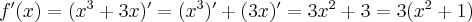
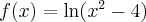
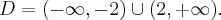

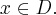
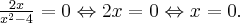
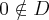
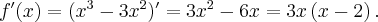
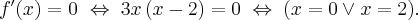
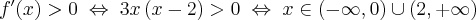
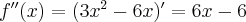
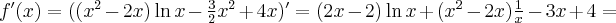
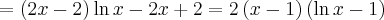
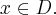
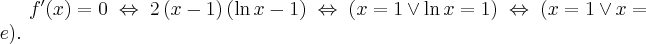
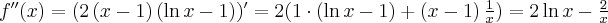
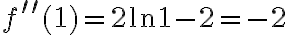
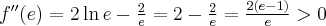
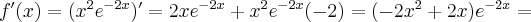
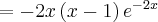
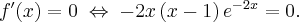
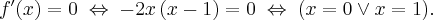
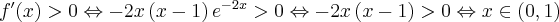
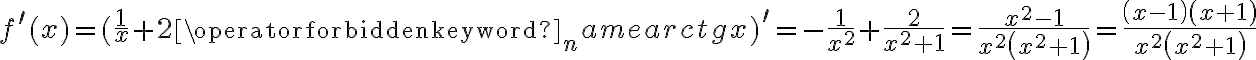
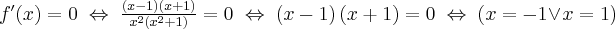
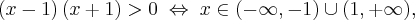
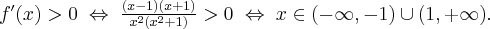
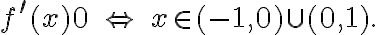
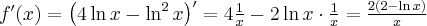
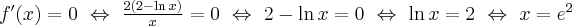
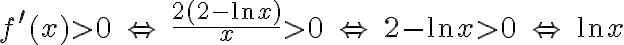
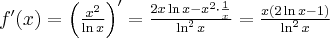
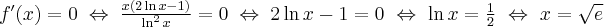
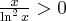
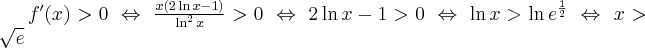
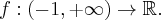
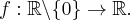
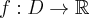
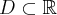
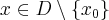




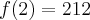
![\displaystyle \max _{x\in \left[-1,2\right]} f(x)=212=f(2) \displaystyle \max _{x\in \left[-1,2\right]} f(x)=212=f(2)](https://port.edu.p.lodz.pl/filter/tex/pix.php/8234effd116b04e91a7f87805d8f4962.png)
![\quad \displaystyle \min _{x\in \left[-1,2\right]} f(x)=-4=f(0) \quad \displaystyle \min _{x\in \left[-1,2\right]} f(x)=-4=f(0)](https://port.edu.p.lodz.pl/filter/tex/pix.php/d2d68bb9e08434d01982aba7b6dd7c6e.png)











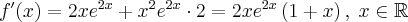




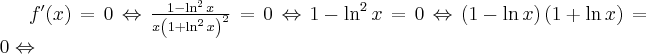





![f^\prime(x)=6-9\cdot \frac{2}{3} x^{-\frac{1}{3}}=6-\frac{6}{\sqrt[3]{x}}, \; x\in \mathbb R\setminus \{0\} f^\prime(x)=6-9\cdot \frac{2}{3} x^{-\frac{1}{3}}=6-\frac{6}{\sqrt[3]{x}}, \; x\in \mathbb R\setminus \{0\}](https://port.edu.p.lodz.pl/filter/tex/pix.php/cb566b4956551492c2b59f07af7ac320.png)
![f^\prime(x)=0 \Leftrightarrow 6-\frac{6}{\sqrt[3]{x}}=0\Leftrightarrow \sqrt[3]{x}=1 \Leftrightarrow x=1 f^\prime(x)=0 \Leftrightarrow 6-\frac{6}{\sqrt[3]{x}}=0\Leftrightarrow \sqrt[3]{x}=1 \Leftrightarrow x=1](https://port.edu.p.lodz.pl/filter/tex/pix.php/3bd36848ca99f6f7ce890b29ed577e59.png)



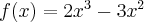
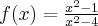
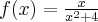
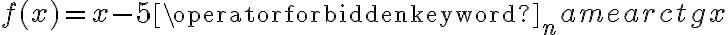
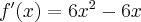
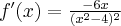
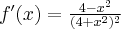
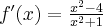
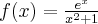
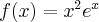
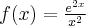
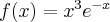
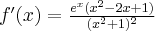
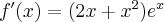
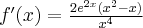
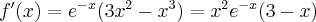

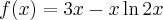
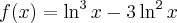

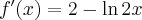
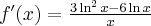
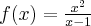
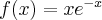
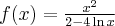
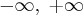
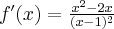
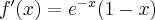
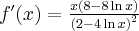
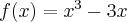
![\left[-\frac32,\frac32\right] \left[-\frac32,\frac32\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/3d37f8f24db07b76ec409152758ed442.png)

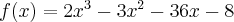
![\left[-3,6\right] \left[-3,6\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/00c68647083b2f383f560b6ad5d18e1c.png)
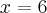
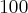
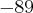
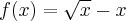
![\left[0,4\right] \left[0,4\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/3a3336efbf8dc022f837ea242eac6177.png)

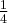

![\left[1,e\right] \left[1,e\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/e39736481a2c1c09c86876a0ced4f203.png)
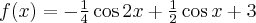
![\left[-\frac\pi2,\pi\right] \left[-\frac\pi2,\pi\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/1486e6af07e678eb58db2c32d27129d2.png)
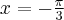
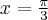

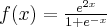
![\left[-1,0\right] \left[-1,0\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/30c62099d861ab81bd5edee7ff9f8135.png)
![\left[-1, 0\right] \left[-1, 0\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/e0ee2ce98c0425348a3c8e433375ea7a.png)
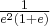
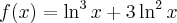
![\left[e^{-3},e^2\right] \left[e^{-3},e^2\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/c58f04d9ed02b443e1d72d25a406c467.png)
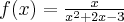
![\left[-2,0\right] \left[-2,0\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/6f7d52e96ec1f58a451ede2a24d276e0.png)
![\left[-2, 0\right] \left[-2, 0\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/344e6b26818e46f5e51bacbcd8fc943f.png)
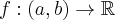
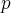
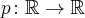
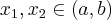
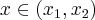
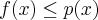
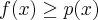
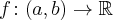




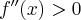


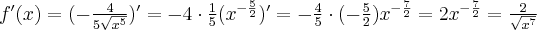










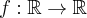
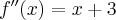
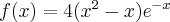
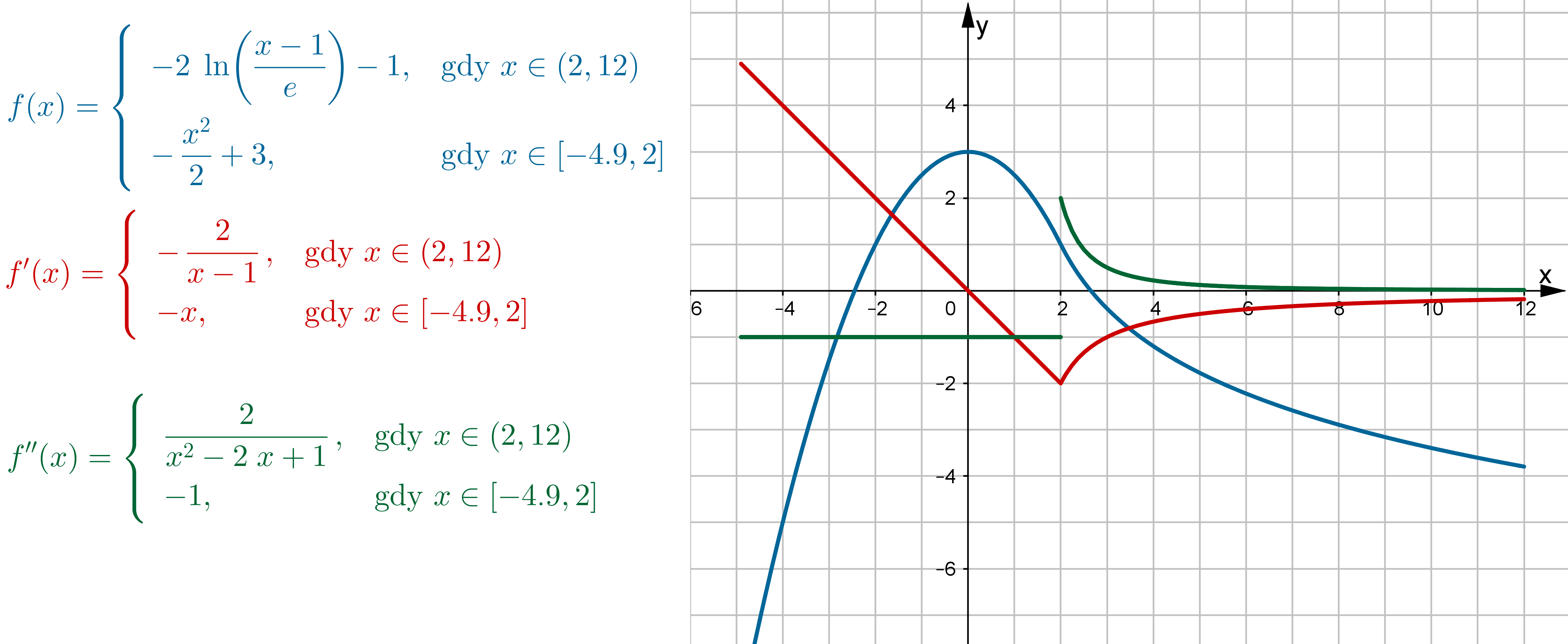
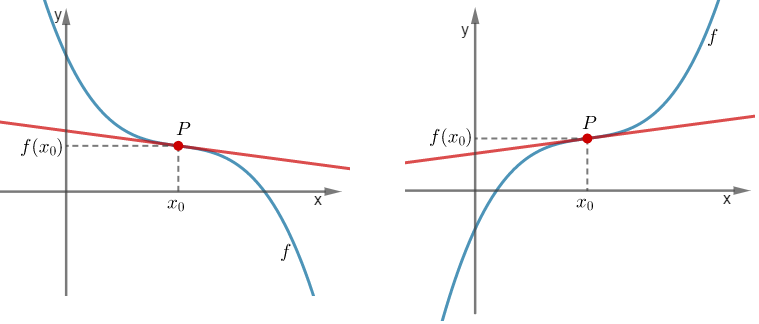
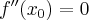
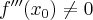






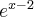

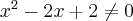









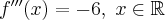

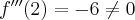



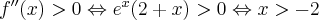

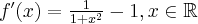






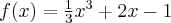
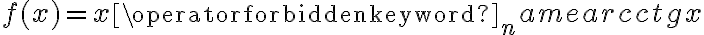
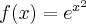
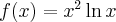
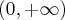
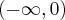
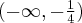
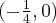
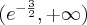
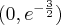
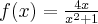
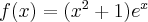
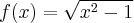
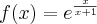
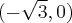
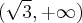
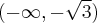
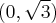
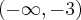
![D=\mathbb{(}-\infty ,-1]\cup \lbrack 1,+\infty ) D=\mathbb{(}-\infty ,-1]\cup \lbrack 1,+\infty )](https://port.edu.p.lodz.pl/filter/tex/pix.php/51b15beb33b9ffe9bea68cdebad4f543.png)
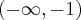
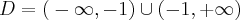
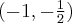
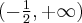
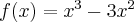
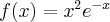
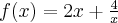
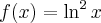
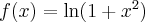
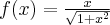
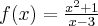
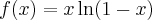


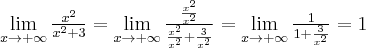



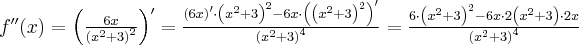






![\lim\limits_{x\to 0^+} \frac{4+\ln x}{x}=\lim\limits_{x\to 0^+} (4+\ln x)\cdot \frac{1}{x}=\left[(4+\ln 0^+)\cdot \frac{1}{0^+}=-\infty\cdot (+\infty)\right]=-\infty \lim\limits_{x\to 0^+} \frac{4+\ln x}{x}=\lim\limits_{x\to 0^+} (4+\ln x)\cdot \frac{1}{x}=\left[(4+\ln 0^+)\cdot \frac{1}{0^+}=-\infty\cdot (+\infty)\right]=-\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/0e15e5c8539e7d53566dd9503d9352ab.png)
![\lim\limits_{x\to+ \infty} \frac{4+\ln x}{x}=\left[\frac{+\infty}{+\infty}\right]\stackrel{[H]}{=}\lim\limits_{x\to +\infty}\frac{\frac1x}{1}=\lim\limits_{x\to +\infty}\frac{1}{x}=\left[\frac{1}{+\infty}\right]=0 \lim\limits_{x\to+ \infty} \frac{4+\ln x}{x}=\left[\frac{+\infty}{+\infty}\right]\stackrel{[H]}{=}\lim\limits_{x\to +\infty}\frac{\frac1x}{1}=\lim\limits_{x\to +\infty}\frac{1}{x}=\left[\frac{1}{+\infty}\right]=0](https://port.edu.p.lodz.pl/filter/tex/pix.php/d9448ffb6c1a09ff78f17d7908456b2a.png)
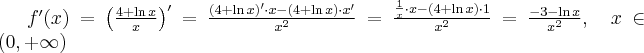
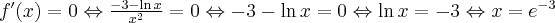

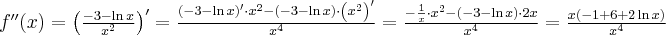





![\lim\limits_{x\to -\infty} f(x)=\lim\limits_{x\to -\infty}\left(3\operatorname{arctg}x-2x\right)=\left[{3\operatorname{arctg}(-\infty)-2\cdot(-\infty)=\frac {-3\pi}{2}}+\infty\right]=+\infty \lim\limits_{x\to -\infty} f(x)=\lim\limits_{x\to -\infty}\left(3\operatorname{arctg}x-2x\right)=\left[{3\operatorname{arctg}(-\infty)-2\cdot(-\infty)=\frac {-3\pi}{2}}+\infty\right]=+\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/30ea6d168837bd5b21d43d217e5e5f44.png)
![\lim\limits_{x\to+ \infty} f(x)=\lim\limits_{x\to+ \infty}\left(3\operatorname{arctg}x-2x\right)=\left[{3\operatorname{arctg}(+\infty)-2\cdot\infty=\frac {3\pi}{2}}-\infty\right]=-\infty \lim\limits_{x\to+ \infty} f(x)=\lim\limits_{x\to+ \infty}\left(3\operatorname{arctg}x-2x\right)=\left[{3\operatorname{arctg}(+\infty)-2\cdot\infty=\frac {3\pi}{2}}-\infty\right]=-\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/467362e47bd4f2af6f66355d15955973.png)

![=\left[\frac{3\operatorname{arctg}(-\infty)}{-\infty}-2 =\frac{-\frac {3\pi}{2}}{-\infty}-2\right] =\left[\frac{3\operatorname{arctg}(-\infty)}{-\infty}-2 =\frac{-\frac {3\pi}{2}}{-\infty}-2\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/62c379a9f7a1cb0b2ce70618ab4d2447.png)



![=\left[3\operatorname{arctg}(-\infty)\right] =\left[3\operatorname{arctg}(-\infty)\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/e03ec2c19fc0a4b8314d1b40ecc1591e.png)


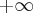

![=\left[\frac{3\operatorname{arctg}(+\infty)}{+\infty}-2=\frac{\frac {3\pi}{2}}{+\infty}-2\right] =\left[\frac{3\operatorname{arctg}(+\infty)}{+\infty}-2=\frac{\frac {3\pi}{2}}{+\infty}-2\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/862e15519d3bf493f62f47ef1bdfe697.png)

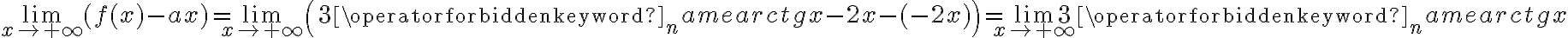
![=\left[3\operatorname{arctg}(+\infty)\right] =\left[3\operatorname{arctg}(+\infty)\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/57cd78e0649f9719d2850057c76120f9.png)
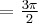

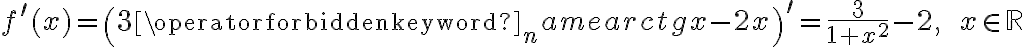







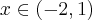
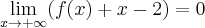

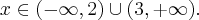

![[-5, 4] [-5, 4]](https://port.edu.p.lodz.pl/filter/tex/pix.php/c1c70481fe548642a4a88044d86f065d.png)
![[-3, 1] [-3, 1]](https://port.edu.p.lodz.pl/filter/tex/pix.php/d2df8b17485bbc7266d72fd130f949fe.png)




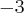






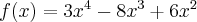
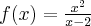
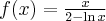
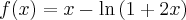

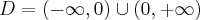
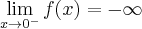

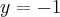

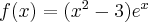















![d(x)=\sqrt{x^2+\tfrac14(x+3)^2(2-x)}=\frac12\sqrt{-x^3+3x+18}, \, x\in [-2,2] d(x)=\sqrt{x^2+\tfrac14(x+3)^2(2-x)}=\frac12\sqrt{-x^3+3x+18}, \, x\in [-2,2]](https://port.edu.p.lodz.pl/filter/tex/pix.php/0961fa07615b6f4fe26e2e047be82b00.png)








![x\in [0,21] x\in [0,21]](https://port.edu.p.lodz.pl/filter/tex/pix.php/a837523de1167fc1a1b5fee332fe474c.png)
![f^\prime (x)=0 \Leftrightarrow \frac{x}{\sqrt{x^{2}+4}}=\frac{21-x}{\sqrt{(21-x)^{2}+144}} \Leftrightarrow \left(\frac{x^2}{x^{2}+4}=\frac{(21-x)^2}{(21-x)^{2}+144} \wedge x\in [0,21]\right). f^\prime (x)=0 \Leftrightarrow \frac{x}{\sqrt{x^{2}+4}}=\frac{21-x}{\sqrt{(21-x)^{2}+144}} \Leftrightarrow \left(\frac{x^2}{x^{2}+4}=\frac{(21-x)^2}{(21-x)^{2}+144} \wedge x\in [0,21]\right).](https://port.edu.p.lodz.pl/filter/tex/pix.php/8c398f262d63e7d9e375ace25222b1bd.png)