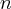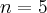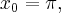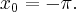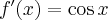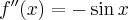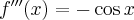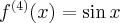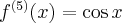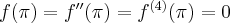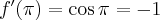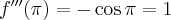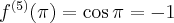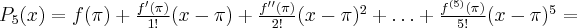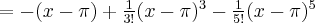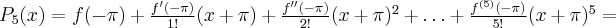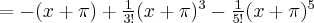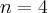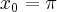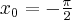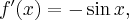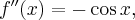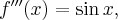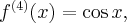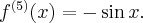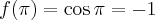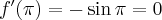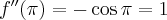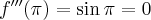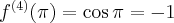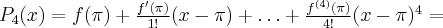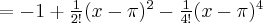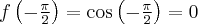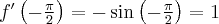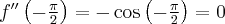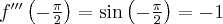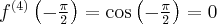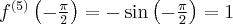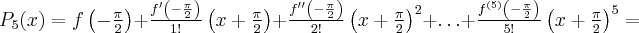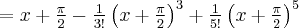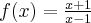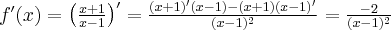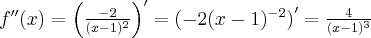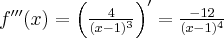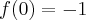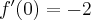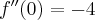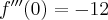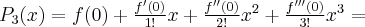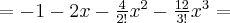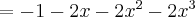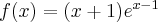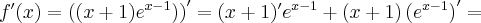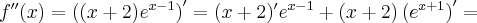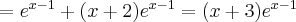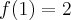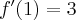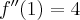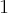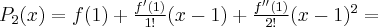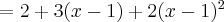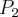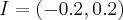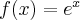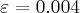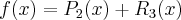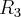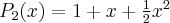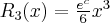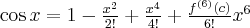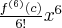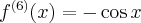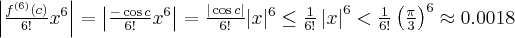2.2 Twierdzenie Taylora
Przykłady
1
Pochodne funkcji 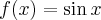 , począwszy od rzędu pierwszego do piątego, są odpowiednio równe
, począwszy od rzędu pierwszego do piątego, są odpowiednio równe
- Wyznaczamy wartość funkcji
 i jej pochodnych dla
i jej pochodnych dla 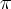 :
:
Zatem wielomianem Taylora stopnia piątego w punkcie
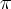 dla funkcji
dla funkcji 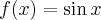 jest
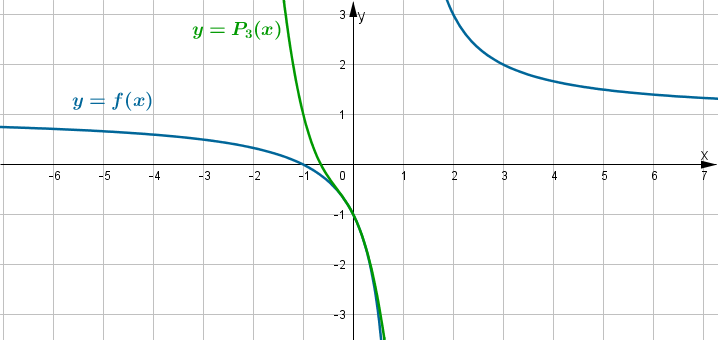
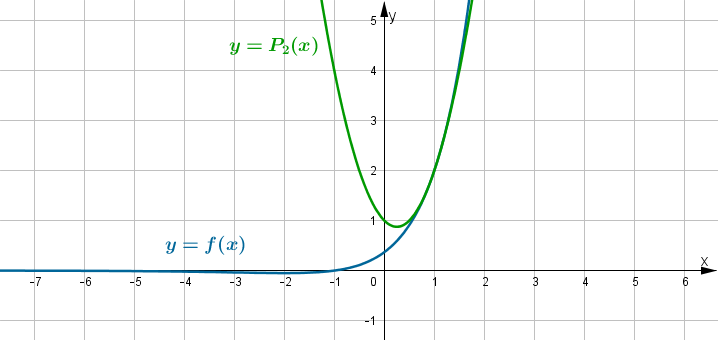
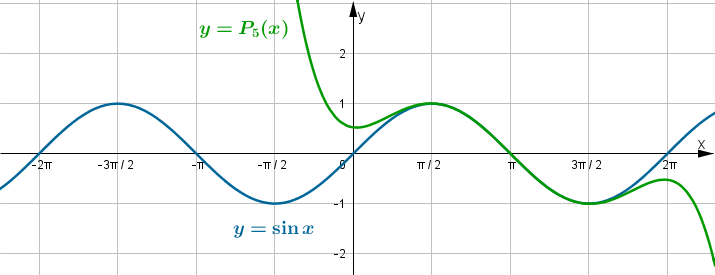
jestPoniżej przedstawiamy wykres funkcji
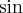 i jej wielomianu Taylora
i jej wielomianu Taylora 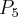 w punkcie
w punkcie 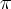 .
.
- Wartości
 i jej pochodnych dla argumentów
i jej pochodnych dla argumentów 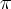 i
i 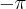 są sobie równe. Stąd wielomianem Taylora stopnia piątego w punkcie
są sobie równe. Stąd wielomianem Taylora stopnia piątego w punkcie 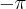 dla funkcji
dla funkcji 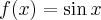 jest
jest
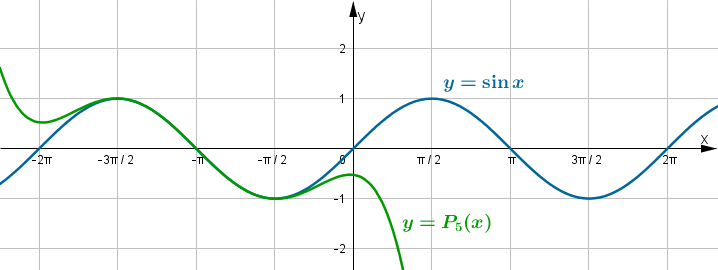
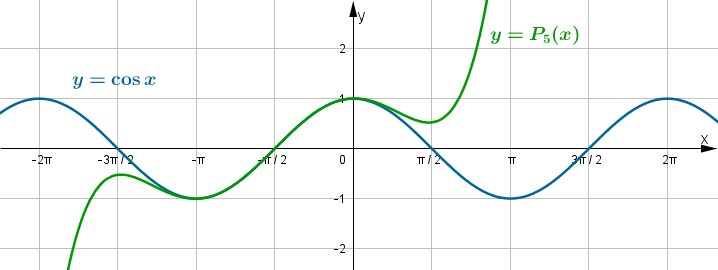
Poniżej znajduje się wykres funkcji
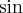 i jej wielomianu Taylora
i jej wielomianu Taylora 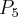 w punkcie
w punkcie 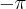 .
.
2
Pochodne funkcji 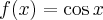 , począwszy od rzędu pierwszego do piątego, są odpowiednio równe
, począwszy od rzędu pierwszego do piątego, są odpowiednio równe
- Wyznaczamy wartość funkcji
 i jej pochodnych dla
i jej pochodnych dla 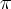 :
:
Zatem wielomianem Taylora stopnia czwartego w punkcie
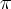 dla funkcji
dla funkcji  jest
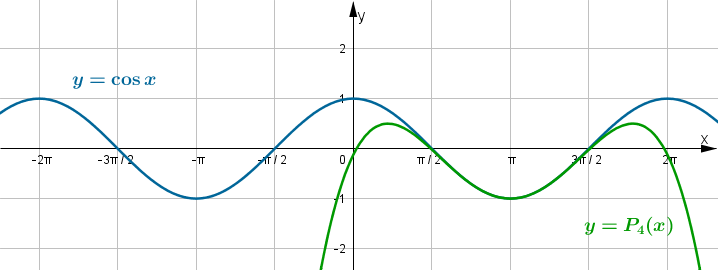
jestPoniżej przedstawiamy wykres funkcji
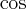 i jej wielomianu Taylora
i jej wielomianu Taylora 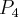 w punkcie
w punkcie 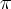 .
.
- Wyznaczamy wartość funkcji
 i jej pochodnych dla
i jej pochodnych dla 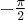 :
:
Wielomianem Taylora stopnia piątego w punkcie
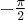 dla funkcji
dla funkcji 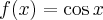 jest więc
jest więcPoniżej przedstawiamy wykres funkcji
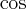 i jej wielomianu Taylora
i jej wielomianu Taylora 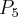 w punkcie
w punkcie 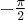 .
.
3
4