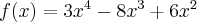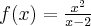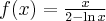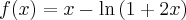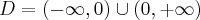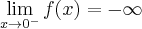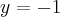6. Badanie przebiegu zmienności funkcji
Zadania
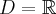 .
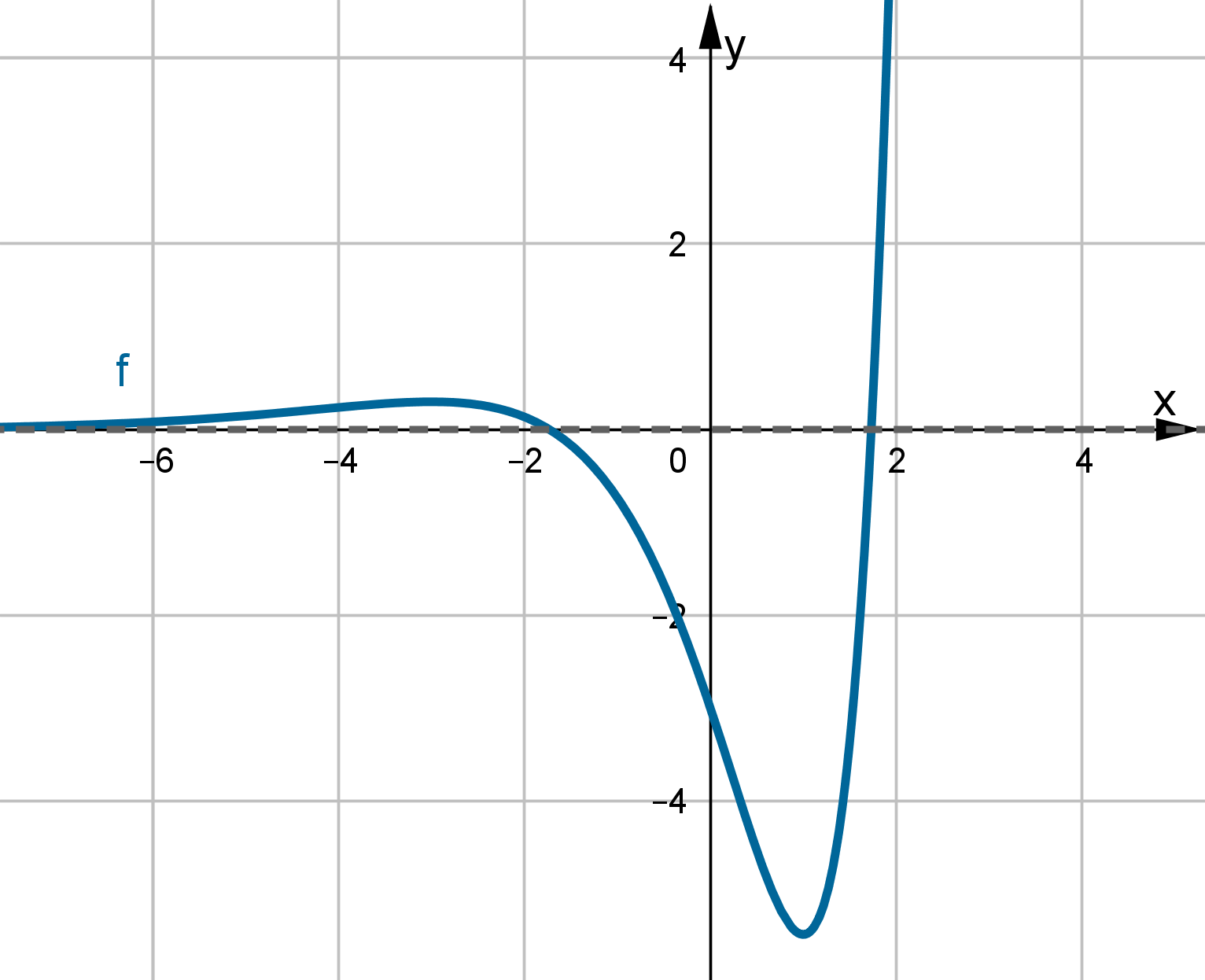
. 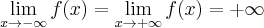 , brak asymptot. Funkcja jest malejąca na przedziale
, brak asymptot. Funkcja jest malejąca na przedziale  , rosnąca na przedziale
, rosnąca na przedziale 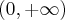 , w punkcie
, w punkcie  funkcja ma minimum lokalne równe
funkcja ma minimum lokalne równe  . Funkcja jest wypukła na każdym z przedziałów:
. Funkcja jest wypukła na każdym z przedziałów: 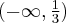 ,
, 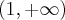 , wklęsła na przedziale
, wklęsła na przedziale  , punkty
, punkty  ,
,  są punktami przegięcia wykresu funkcji.
są punktami przegięcia wykresu funkcji.

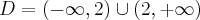 . Wykres funkcji ma asymptotę pionową obustronną
. Wykres funkcji ma asymptotę pionową obustronną  ,
, 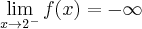 ,
, 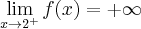 , oraz asymptotę ukośną o równaniu
, oraz asymptotę ukośną o równaniu 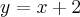 w
w 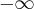 i
i 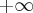 . Funkcja jest rosnąca na każdym z przedziałów:
. Funkcja jest rosnąca na każdym z przedziałów:  ,
, 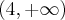 , malejąca na każdym z przedziałów
, malejąca na każdym z przedziałów 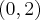 ,
, 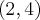 , w punkcie
, w punkcie  funkcja ma maksimum lokalne równe
funkcja ma maksimum lokalne równe  , w punkcie
, w punkcie 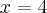 funkcja ma minimum lokalne równe
funkcja ma minimum lokalne równe  . Funkcja jest wklęsła na przedziale
. Funkcja jest wklęsła na przedziale  , wypukła na przedziale
, wypukła na przedziale 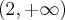 , brak punktów przegięcia.
, brak punktów przegięcia.
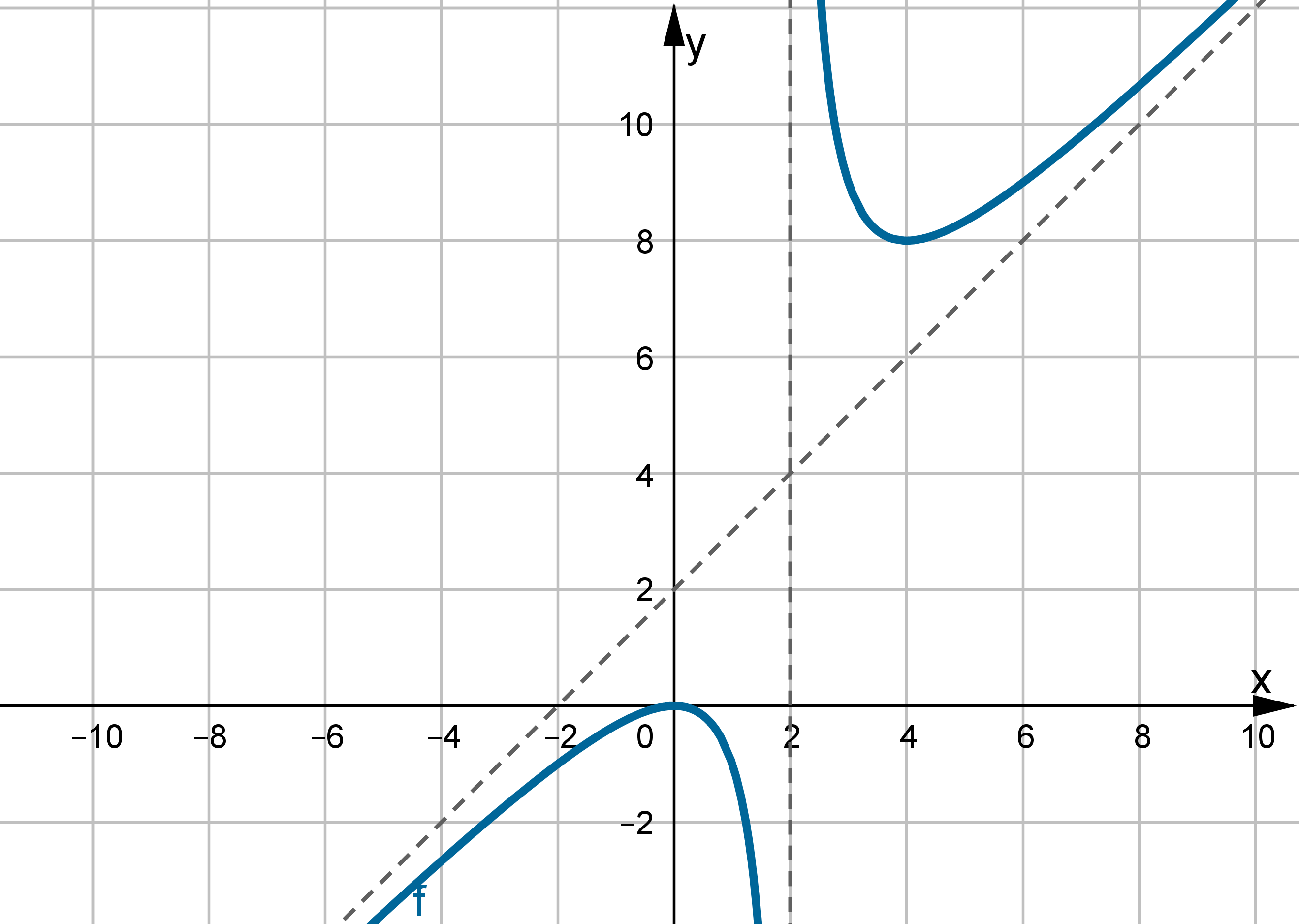
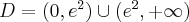 .
. 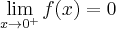 , wykres funkcji ma asymptotę pionową obustronną
, wykres funkcji ma asymptotę pionową obustronną 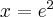 ,
, 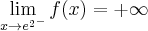 ,
, 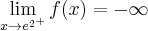 ,
, 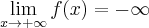 , brak asymptoty ukośnej. Funkcja jest rosnąca na każdym z przedziałów:
, brak asymptoty ukośnej. Funkcja jest rosnąca na każdym z przedziałów: 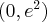 ,
, 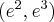 , malejąca na przedziale
, malejąca na przedziale 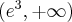 , w punkcie
, w punkcie 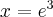 funkcja ma maksimum lokalne równe
funkcja ma maksimum lokalne równe  . Funkcja jest wypukła na każdym z przedziałów
. Funkcja jest wypukła na każdym z przedziałów 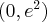 ,
, 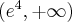 , wklęsła na przedziale
, wklęsła na przedziale 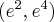 , punkt
, punkt 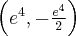 jest punktem przegięcia wykresu funkcji.
jest punktem przegięcia wykresu funkcji.
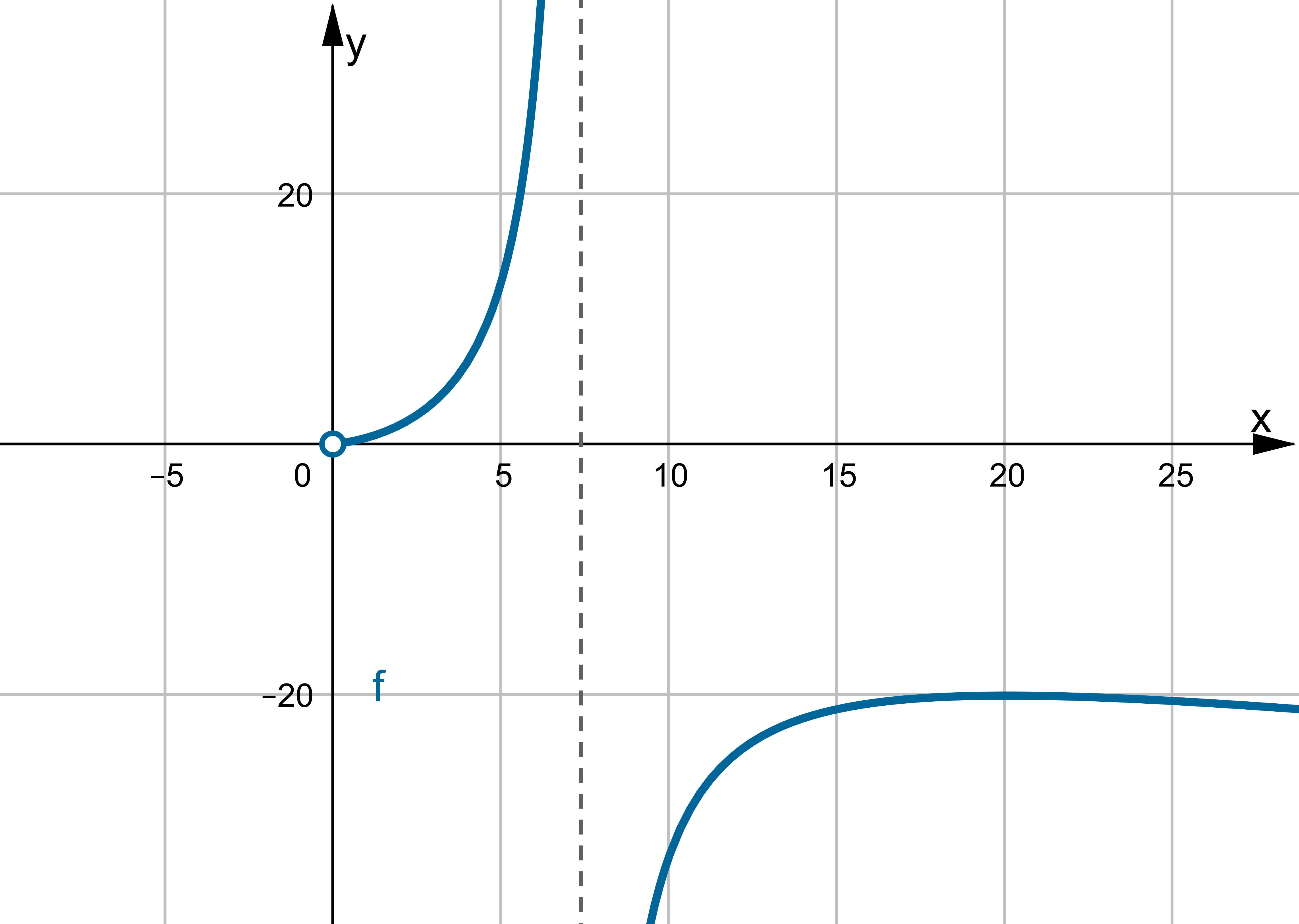
 . Wykres funkcji ma asymptotę pionową prawostronną
. Wykres funkcji ma asymptotę pionową prawostronną 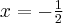 ,
, 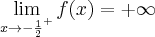 ,
, 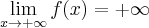 , brak asymptoty ukośnej. Funkcja jest malejąca na przedziale
, brak asymptoty ukośnej. Funkcja jest malejąca na przedziale 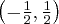 , rosnąca na przedziale
, rosnąca na przedziale 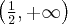 , w punkcie
, w punkcie  funkcja ma minimum lokalne równe
funkcja ma minimum lokalne równe 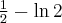 . Funkcja jest wypukła w całej dziedzinie.
. Funkcja jest wypukła w całej dziedzinie.

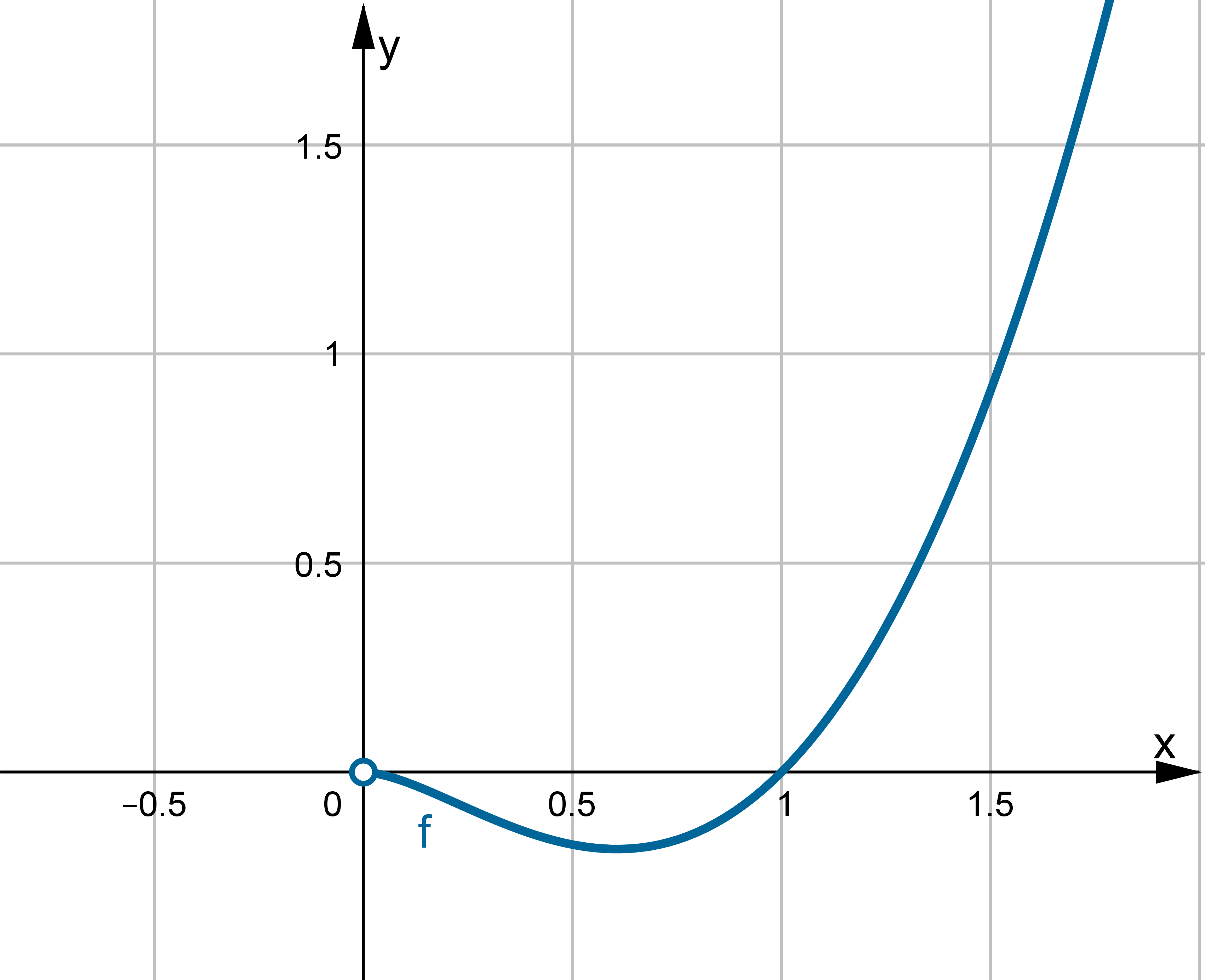
 .
. 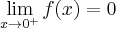 ,
, 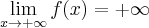 , brak asymptot. Funkcja jest malejąca na przedziale
, brak asymptot. Funkcja jest malejąca na przedziale 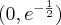 , rosnąca na przedziale
, rosnąca na przedziale  , w punkcie
, w punkcie 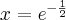 funkcja ma minimum lokalne równe
funkcja ma minimum lokalne równe 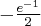 . Funkcja jest wypukła na przedziale:
. Funkcja jest wypukła na przedziale: 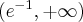 , wklęsła na przedziale
, wklęsła na przedziale 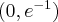 , punkt
, punkt 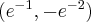 jest punktem przegięcia wykresu funkcji.
jest punktem przegięcia wykresu funkcji.
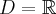 . Wykres funkcji ma asymptotę poziomą
. Wykres funkcji ma asymptotę poziomą 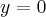 w
w 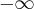 ,
, 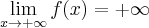 . Funkcja jest malejąca na przedziale
. Funkcja jest malejąca na przedziale  , rosnąca na każdym z przedziałów
, rosnąca na każdym z przedziałów 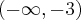 ,
, 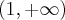 , w punkcie
, w punkcie 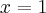 funkcja ma minimum lokalne równe
funkcja ma minimum lokalne równe  , w punkcie
, w punkcie  funkcja ma maksimum lokalne równe
funkcja ma maksimum lokalne równe  . Funkcja jest wypukła na każdym z przedziałów:
. Funkcja jest wypukła na każdym z przedziałów: 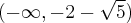 ,
,  , wklęsła na przedziale
, wklęsła na przedziale  , punkty
, punkty 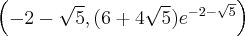 ,
, 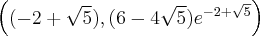 są punktami przegięcia wykresu funkcji.
są punktami przegięcia wykresu funkcji.