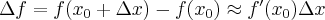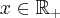Rachunek różniczkowy funkcji jednej zmiennej

 

Zauważmy, że dla funkcji jednej zmiennej $f(x)$, dla małych przyrostów $\Delta x$ mamy:

$\Delta f=f(x_{0}+\Delta x)-f(x_{0})\approx f'(x_{0})\Delta x$.

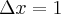Niech $\Delta x=1$, czyli argument zwiększa się o jednostkę w stosunku do poziomu wyjściowego. Wtedy powyższa zależność ma postać:

$\Delta f=f(x_{0}+1)-f(x_{0})\approx f'(x_{0})$,

czyli zwiększenie argumentu o jednostkę powoduje wzrost funkcji o $f′(x_0)$. Zatem wielkość krańcowa funkcji jest w przybliżeniu równa przyrostowi funkcji przy wzroście argumentu funkcji o jednostkę. Wielkość krańcowa jest miarą szybkości zmian wartości funkcji w punkcie $x_0$.

 

Przykłady

 

1. Funkcja kosztu

Koszt wytworzenia dowolnej wielkości produkcji zależy od wielkości nakładów poszczególnych czynników produkcji oraz ich cen. Jest on więc funkcją kilku zmiennych. Jeżeli jednak nasze rozważania ograniczymy do krótkiego okresu, a więc czasu, w którym przynajmniej jeden czynnik produkcji jest stały i koszt możemy przedstawić jako funkcję jednej zmiennej: wielkości produkcji.

Koszty całkowite są sumą kosztów stałych i kosztów zmiennych.

Niech $K:\mathbb R_+\to\mathbb R_+$ będzie funkcją kosztu całkowitego zależną od wielkości produkcji $x$, gdzie $x\in(0,+\infty)$. Wtedy funkcję

$K_{p}:x\to K_{p}\left( x\right) =\frac{K(x)}{x}$

nazywamy funkcją kosztów przeciętnych, a jej wartość 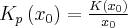$K_{p}\left( x_{0}\right) =\frac{K(x_{0})}{x_{0}}$ kosztem przeciętnym (jednostkowym) wytworzenia jednostki produktu przy poziomie produkcji $x_0$.

Przy podejmowaniu decyzji dotyczących wielkości produkcji (i jej wpływu na koszty) bardzo ważną wskazówką jest kształtowanie się kosztów jednostkowych przy różnych rozmiarach produkcji. W tego typu analizach przydatne jest wykorzystanie kosztów krańcowych.

 

Przy założeniu, że funkcja $K(x)$ jest różniczkowalna oraz $x_0>0$, $\Delta x>0$, $x_0+\Delta x>0$, gdzie $\Delta x$ jest dodatnim przyrostem argumentu funkcji (przyrostem produkcji), można zbudować iloraz różnicowy (przyrost przeciętny) tej funkcji:

$\frac{K(x_{0}+\Delta x)-K(x_{0})}{\Delta x}=\frac{\Delta K}{\Delta x}$.

Wyraża on przeciętny koszt wytworzenia dodatkowych jednostek produktu $\Delta x$ poczynając od poziomu $x_0$. Granicą tego ilorazu jest pochodna funkcji $K$ w punkcie $x_0$

$K'(x_{0})=\underset{\Delta x\rightarrow 0}{\lim }\frac{\Delta K}{\Delta x}.$

Stąd

$K_{x}(x_0)=K'(x_0)$.

Natomiast funkcja 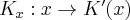$K_{x}: x\to K'(x)$ jest funkcją kosztu krańcowego.

 

2. Funkcja produkcji

Funkcja produkcji określa relacje między wielkością produkcji a liczbą zaangażowanych czynników produkcji. Funkcja produkcji określa, jaką maksymalną wielkość produkcji może osiągnąć przedsiębiorstwo w wyniku użycia posiadanych zasobów, przy danej technice wytwarzania.

Funkcja produkcji

$TP=f(K,L), \ \ \ \ K\geq 0,\ L\geq 0$,

gdzie: $TP$ ‒ całkowita wielkość produkcji; $K$ ‒ ilość użytych jednostek kapitału; $L$ ‒ ilość użytych jednostek pracy.

Jak widać (po uproszczeniu) produkcja zależy od zaangażowanych w nią kapitału i pracy. Krótki okres (SR) to taki czas (stan), w którym ilość jednego lub więcej czynników produkcji jest stała (przynajmniej jeden czynnik produkcji jest stały, pozostałe mogą być zmienne).

 

Prawo malejących dochodów głosi, że jeżeli następuje wzrost nakładów jednego czynnika produkcji (przy założeniu stałości pozostałych czynników), to począwszy od pewnego poziomu, przyrosty produkcji zaczynają maleć. Formuła liczenia:

$MP=TP'=\frac{\Delta TP}{\Delta L}$.

 

3. Funkcja konsumpcji

Dochody gospodarstw domowych mają być przeznaczone na wydatki konsumpcyjne lub na oszczędności $Y=C+S$. Przy danym poziomie dochodów im większe wydatki konsumpcyjne, tym mniejsze oszczędności i odwrotnie, im większe oszczędności, tym mniejsze wydatki konsumpcyjne. Wynika z tego, że decyzje gospodarstw domowych w sprawie wydatków konsumpcyjnych są zarazem decyzjami w sprawie oszczędzania. Funkcja konsumpcji pokazuje poziom zamierzonych łącznych wydatków konsumpcyjnych przy różnych poziomach dochodu. Zależność (liniową) między wydatkami konsumpcyjnymi a dochodem charakteryzuje skłonność do konsumpcji.

• Przeciętna skłonność do konsumpcji to stosunek wydatków konsumpcyjnych do dochodu. Wielkość ta informuje, jaka części dochodu przeznaczona jest na konsumpcję: $\frac{C}{Y}$.
• Krańcowa skłonność do konsumpcji to stosunek przyrostu wydatków konsumpcyjnych do przyrostu dochodu. Wielkość ta informuje jaka część przyrostu dochodu przeznaczona jest na wydatki konsumpcyjne:

  $K_{sk}=\frac{\Delta C}{\Delta Y}$.

W polityce gospodarczej znajomość krańcowej skłonności do konsumpcji ma duże znaczenie. Pozwala bowiem odpowiedzieć, z dużą dozą prawdopodobieństwa, na co ludzie przeznaczą dodatkowe dochody i w jakiej proporcji wydadzą je na dobra konsumpcyjne, a ile zaoszczędzą.

 

4. Funkcja użyteczności

Funkcja użyteczności to funkcja, której wartościami są wartości użyteczności (satysfakcji, komfortu psychicznego). Można mówić o użyteczności różnych zjawisk (koszyków towarów). Użyteczność pieniądza (bogactwa) jest np. funkcją, która wartości pieniężnej przyporządkowuje użyteczność dla otrzymującego tę wartość. Funkcja użyteczności jest pojęciem psychologicznym, co oznacza, że każdy ma swoją funkcję użyteczności. Jednak pewne ogólne własności są wspólne. Mianowicie, ponieważ każdy woli posiadać więcej niż mniej, więc funkcja użyteczności jest rosnąca. Ponadto krańcowa użyteczność jest malejąca, tzn. każdy dodatkowy procent wzrostu bogactwa powoduje coraz mniejszy przyrost użyteczności. Przykładowo, ktoś kto nic nie ma, podejmie wysiłek w celu zarobienia $10$ zł., bo ta kwota zapewni mu np. posiłek. Dla osoby bogatej ta kwota będzie prawie bez znaczenia.

Funkcja użyteczności 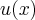$u(x)$ jest funkcją spełniającą warunki:

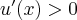• $u'(x) > 0$ ‒ postulat niedosytu oznacza, że wzrost ilości towaru w koszyku zwiększa użyteczności koszyka,
• $u''(x) < 0$ ‒ krańcowa użyteczność każdego towaru maleje, w miarę jak wzrasta jego spożycie.

Określa ona użyteczność posiadania przez osobę/instytucję wartości (pieniężnej) $x$.