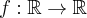5.2 Punkty przegięcia wykresu funkcji
Ćwiczenia interaktywne, cz.1
Przypomnij sobie:
• definicję punktu przegięcia • warunek konieczny istnienia punktu przegięcia • I warunek wystarczający istnienia punktu przegięcia • II warunek wystarczający istnienia punktu przegięcia
1
Zastanów się, jakie punkty przegięcia posiadają funkcje o przedstawionych wykresach.
2
Przyporządkuj podane funkcje do odpowiedniej grupy.
3
Dopasuj do funkcji punkty przegięcia ich wykresów.
4
Zaznacz punkty przegięcia wykresu funkcji.
5
6
7
8
9