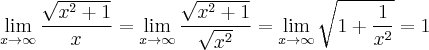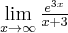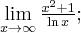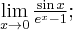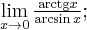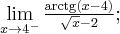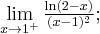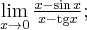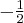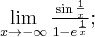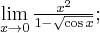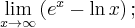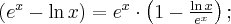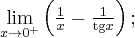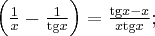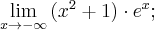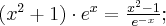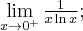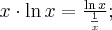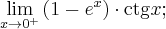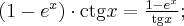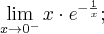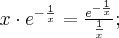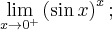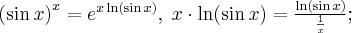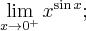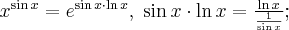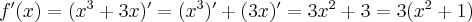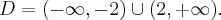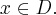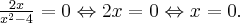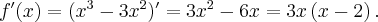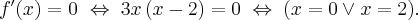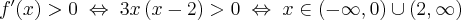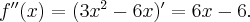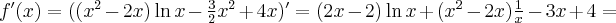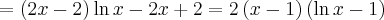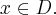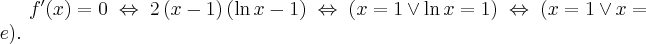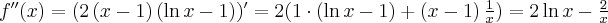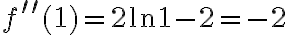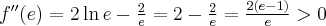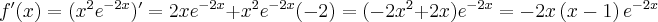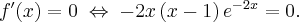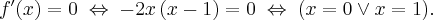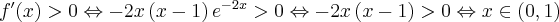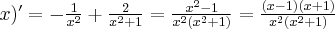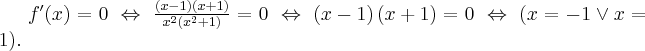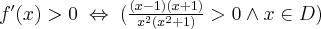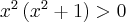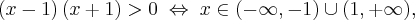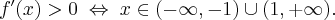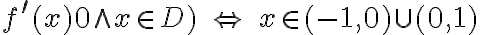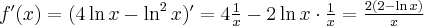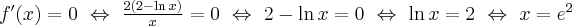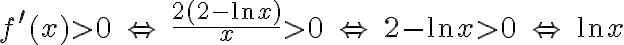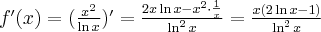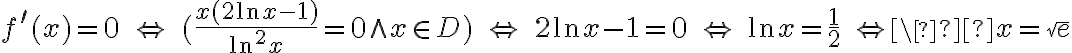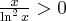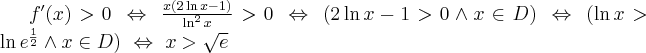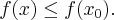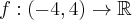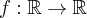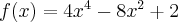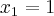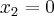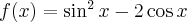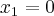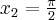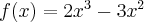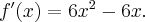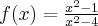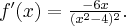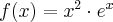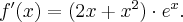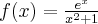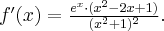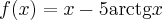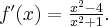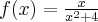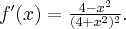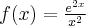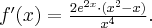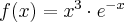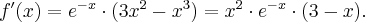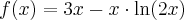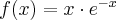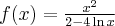Pochodna funkcji jednej zmiennej -5sty
| Site: | WIKAMP Port |
| Course: | Pochodna funkcji jednej zmiennej |
| Book: | Pochodna funkcji jednej zmiennej -5sty |
| Printed by: | Gość |
| Date: | Monday, 19 January 2026, 8:21 PM |
1. Wprowadzenie
W tym rozdziale poznamy:
- definicję pochodnej funkcji w punkcie
- definicję pochodnej jako funkcji
- interpretację geometryczną, fizyczną i ekonomiczną pochodnej funkcji w punkcie.
Nauczymy się jak
- badać istnienie pochodnej funkcji w punkcie korzystając z definicji
- liczyć pochodną funkcji korzystając ze wzorów (w tym pochodną funkcji złożonej i funkcji odwrotnej)
- wyznaczać równanie stycznej do wykresu funkcji w punkcie.
Film:
1.1 Pochodna funkcji w punkcie
...
Teoria
Definicja 1 Załóżmy, że funkcja  jest określona na pewnym otoczeniu
jest określona na pewnym otoczeniu 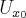 punktu
punktu  . Niech
. Niech 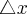 będzie różnym od zera przyrostem zmiennej
będzie różnym od zera przyrostem zmiennej  takim, że
takim, że 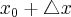 należy do tego otoczenia. Niech
należy do tego otoczenia. Niech 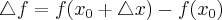 będzie przyrostem wartości funkcji odpowiadającym przyrostowi
będzie przyrostem wartości funkcji odpowiadającym przyrostowi 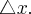 Ilorazem różnicowym funkcji
Ilorazem różnicowym funkcji  w punkcie
w punkcie  dla przyrostu
dla przyrostu 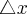 nazywamy wyrażenie
nazywamy wyrażenie
Jeżeli istnieje i jest skończona granica
to nazywamy ją pochodną funkcji  w punkcie
w punkcie  i oznaczamy
i oznaczamy  lub
lub  .
.
Zatem
(o ile granica ta istnieje i jest skończona).
Uwaga 1 Iloraz różnicowy może być także zapisany w postaci
Wówczas pochodna funkcji  w punkcie
w punkcie  ma postać
ma postać
Definicja 2 Załóżmy, że funkcja  jest określona na pewnym prawostronnym otoczeniu
jest określona na pewnym prawostronnym otoczeniu  . Niech
. Niech 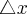 będzie różnym od zera przyrostem zmiennej
będzie różnym od zera przyrostem zmiennej  takim, że
takim, że 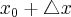 należy do tego otoczenia. Niech
należy do tego otoczenia. Niech 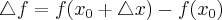 będzie przyrostem funkcji odpowiadającym przyrostowi
będzie przyrostem funkcji odpowiadającym przyrostowi 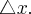 Jeżeli istnieje i jest skończona granica
Jeżeli istnieje i jest skończona granica
to nazywamy ją pochodną prawostronną funkcji  w punkcie
w punkcie  i oznaczamy
i oznaczamy 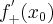 lub
lub 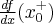 . Zatem
. Zatem
Uwaga 2 Pochodna prawostronna funkcji  w punkcie
w punkcie  może być także zapisana w postaci
może być także zapisana w postaci
Definicja 3 Załóżmy, że funkcja  jest określona na pewnym lewostronnym otoczeniu
jest określona na pewnym lewostronnym otoczeniu  . Niech
. Niech 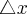 będzie różnym od zera przyrostem zmiennej
będzie różnym od zera przyrostem zmiennej  takim, że
takim, że 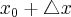 należy do tego otoczenia. Niech
należy do tego otoczenia. Niech 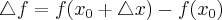 będzie przyrostem funkcji odpowiadającym przyrostowi
będzie przyrostem funkcji odpowiadającym przyrostowi 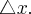 Jeżeli istnieje i jest skończona granica
Jeżeli istnieje i jest skończona granica
to nazywamy ją pochodną lewostronną funkcji  w punkcie
w punkcie  i oznaczamy
i oznaczamy 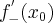 lub
lub 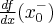 . Zatem
. Zatem
Uwaga 3 Pochodna lewostronna funkcji  w punkcie
w punkcie  może być także zapisana w postaci
może być także zapisana w postaci
Twierdzenie 1 Warunek konieczny i wystarczający istnienia pochodnej w punkcie Funkcja  ma pochodną w punkcie
ma pochodną w punkcie  wtedy i tylko wtedy, gdy istnieją i są sobie równe pochodne jednostronne funkcji
wtedy i tylko wtedy, gdy istnieją i są sobie równe pochodne jednostronne funkcji  w punkcie
w punkcie  . Wówczas
. Wówczas
Definicja 4 Załóżmy, że funkcja  jest określona i ciągła na pewnym otoczeniu punktu
jest określona i ciągła na pewnym otoczeniu punktu  . Mówimy, że funkcja
. Mówimy, że funkcja  ma pochodną niewłaściwą w punkcie
ma pochodną niewłaściwą w punkcie  , gdy
, gdy
Wówczas piszemy
Definicja 5 Załóżmy, że funkcja  jest określona i ciągła na pewnym prawostronnym otoczeniu punktu
jest określona i ciągła na pewnym prawostronnym otoczeniu punktu  . Mówimy, że funkcja
. Mówimy, że funkcja  ma pochodną niewłaściwą prawostronną w punkcie
ma pochodną niewłaściwą prawostronną w punkcie  , gdy
, gdy
Wówczas piszemy
Definicja 6 Załóżmy, że funkcja  jest określona i ciągła na pewnym lewostronnym otoczeniu punktu
jest określona i ciągła na pewnym lewostronnym otoczeniu punktu  . Mówimy, że funkcja
. Mówimy, że funkcja  ma pochodną niewłaściwą prawostronną w punkcie
ma pochodną niewłaściwą prawostronną w punkcie  , gdy
, gdy
Wówczas piszemy
Definicja 7 Załóżmy, że funkcja f jest określona, ciągła i ma pochodną w każdym punkcie x zbioru A. Funkcję
nazywamy funkcją pochodną lub pochodną funkcji  na zbiorze A.
na zbiorze A.
Definicja 8 Funkcję jednej zmiennej, która ma pochodną w punkcie  nazywamy funkcją różniczkowalną w tym punkcie.
nazywamy funkcją różniczkowalną w tym punkcie.
Twierdzenie 2 Jeżeli funkcja  jest różniczkowalna w punkcie
jest różniczkowalna w punkcie  , to jest ciągła w tym punkcie.
, to jest ciągła w tym punkcie.
Uwaga 4 Implikacja odwrotna nie zachodzi, tzn. nie jest prawdą, że jeżeli funkcja jest ciągła w punkcie  , to jest różniczkowalna w tym punkcie. Przykładem funkcji, która jest ciągła i nieróżniczkowalna w
, to jest różniczkowalna w tym punkcie. Przykładem funkcji, która jest ciągła i nieróżniczkowalna w  jest
jest  .
.
Przykłady
Przykład 1
Korzystając z definicji obliczymy pochodną funkcji 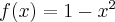 w punkcie
w punkcie 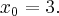
Rozw.
Przykład 2
Obliczymy teraz pochodne jednostronne funkcji 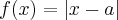 w punkcie
w punkcie 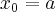 , gdzie
, gdzie 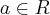 .
.
Rozw.
Iloraz różnicowy ma postać:
Korzystając z definicji modułu mamy
Obliczamy teraz
Czyli
zatem nie istnieje pochodna funkcji w punkcie 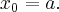
Przykład 3
Obliczymy pochodną funkcji  w dowolnym punkcie
w dowolnym punkcie 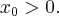
Rozw.
Czyli
Ćwiczenia interaktywne
...
1.2 Reguły różniczkowania
...
Teoria
...
Przykłady
...
1.3 Interpretacja geometryczna pochodnej w punkcie
...
Teoria
...
Przykłady
...
Ćwiczenia interaktywne
...
1.4 Interpretacja fizyczna i ekonomiczna pochodnej w punkcie
...
Teoria
...
Przykłady
...
1.5 Zadania
Film
Film (z teorią)
W tym rozdziale poznamy:
- ?związek pomiędzy monotonicznością funkcji a jej pochodną
- definicję ekstremów lokalnych
- związki pomiędzy istnieniem ekstremów lokalnych a pochodną funkcji
- definicję ekstremów globalnych
- algorytm wyznaczania ekstremów globalnych
Nauczymy się jak
- badać monotoniczność funkcji
- wyznaczać ekstrema lokalne korzystając z pierwszego lub drugiego warunku wystarczającego
- wyznaczać ekstrema globalne
2. Twierdzenia o wartości średniej i wnioski z nich
W tym rozdziale poznamy:
- twierdzenie Rolle'a
- tw. Lagrange'a
- wnioski z tw. L dotyczące monotoniczności
- reguły de l'Hospitala
- tw. Taylora.
Nauczymy się jak
2.1 Twierdzenie Rolle'a i Lagrange'a
...
Teoria
...
Przykłady
...
Ćwiczenia interaktywne
...
2.2 Reguła de l'Hospitala (*)
..
Teoria
Twierdzenie -- reguła de l'Hospitala.
Niech funkcje 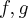 będą różniczkowalne na pewnym sąsiedztwie punktu
będą różniczkowalne na pewnym sąsiedztwie punktu  . Jeżeli
. Jeżeli
to istnieje granica  , przy czym
, przy czym
Uwaga 1. Powyższe twierdzenie dotyczy symbolu nieoznaczonego typu  , ale przy odpowiedniej zmianie założeń pozostaje prawdziwe dla symbolu
, ale przy odpowiedniej zmianie założeń pozostaje prawdziwe dla symbolu 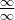 oraz dla granic jednostronnych i granic w
oraz dla granic jednostronnych i granic w  .
.
Uwaga 2. Regułę można także stosować do pozostałych symboli nieoznaczonych, po sprowadzeniu ich do symbolu  lub
lub 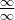 w następujący sposób:
w następujący sposób:
Przykłady
Przykład 1
Obliczymy granice funkcji:
a) Zaczynamy od określenia symbolu granicy, aby zdecydować, czy można zastosować regułę de l'Hospitala.
Następnie badamy, czy istnieje granica ilorazu pochodnych:
Na mocy reguły de l'Hospitala otrzymujemy odpowiedź
Zwykle stosując regułę de l'Hospitala stosujemy uproszczony zapis, przedstawiony w rozwiązaniu kolejnego zadania.
c) Określamy symbol badanej granicy:
Symbol granicy jest oznaczony, a zatem w tym przypadku nie można wykorzystać reguły de l'Hospitala. Aby obliczyć granicę należy zastosować odpowiednie twierdzenia arytmetyki granic funkcji:
Na koniec zauważmy, że w tym przypadku
a zatem granica ilorazu pochodnych różni się od badanej granicy.
Przykład 2
Obliczymy granice funkcji:
b) W przypadku tej granicy regułę de l'Hospitala zastosujemy dwukrotnie:
Wykorzystaliśmy tutaj fakt, że  .
.
Przykład 3
Obliczymy granice funkcji:
Rozwiązanie
Podobnie jak w poprzednich przykładach zaczynamy od określenia symbolu badanej granicy
przy czym 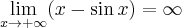 na mocy twierdzenia o dwóch ciągach.
na mocy twierdzenia o dwóch ciągach.
W tym przypadku nie możemy wykorzystać reguły de l'Hospitala, gdyż
zaś taka granica nie istnieje. Nie oznacza to jednak, że nie istnieje badana granica -- trzeba tylko policzyć ją innym sposobem. Ponieważ
więc na mocy twierdzenia o trzech ciągach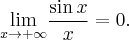
b) W tym przypadku
a zatem stosowanie reguły de l'Hospitala nie jest efektywne. Granicę funkcji możemy jednak obliczyć w inny sposób:
Ćwiczenia interaktywne
Ćwiczenie 1a
W przypadku których z poniższych symboli granic funkcji możemy bezpośrednio zastosować regułę de l'Hospitala?
Ćwiczenie 1b
Określ, czy podany symbol granicy jest oznaczony, czy nieoznaczony oraz czy możemy w takiej sytuacji bezpośrednio zastosować regułę de l'Hospitala:
Ćwiczenie 2
Oblicz podane granice.
Uzupełnij puste pola.
Ćwiczenie 3
Oblicz podane granice. Czy i ile razy stosowałeś regułę de l'Hospitala?
Przeciągnij i upuść poprawne odpowiedzi.
Ćwiczenie 4
Oblicz podane granice. Czy i ile razy stosowałeś regułę de l'Hospitala?
Przeciągnij i upuść poprawne odpowiedzi.
2.3 Zadania
Zadanie 1.
Stosując regułę de l'Hospitala oblicz granice funkcji:
Zadanie 2.
Oblicz granice funkcji:
3. Monotoniczność funkcji, ekstrema lokalne i ekstrema globalne
...
3.1 Badanie monotoniczności funkcji (*)
..
Teoria
..
Przykłady
..
Ćwiczenia interaktywne
...
3.2 Ekstrema lokalne funkcji (*)
...
Przykłady
Przykład 1
Wykażemy, że funkcja określona wzorem 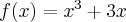 nie posiada ekstremów lokalnych.
nie posiada ekstremów lokalnych.
Funkcja  jest wielomianem, zatem dziedziną funkcji jest zbiór
jest wielomianem, zatem dziedziną funkcji jest zbiór 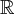 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
Ponieważ 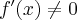 dla
dla  , więc
, więc  nie ma punktów stacjonarnych i w konsekwencji nie ma też ekstremów lokalnych (stosujemy wniosek z warunku koniecznego istnienia ekstremum lokalnego).
nie ma punktów stacjonarnych i w konsekwencji nie ma też ekstremów lokalnych (stosujemy wniosek z warunku koniecznego istnienia ekstremum lokalnego).
Przykład 2
Wykażemy, że funkcja określona wzorem 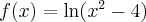 nie posiada ekstremów lokalnych.
nie posiada ekstremów lokalnych.
Obliczamy pochodną funkcji:
Wyznaczamy punkty stacjonarne funkcji  rozwiązując równanie:
rozwiązując równanie: 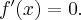
Jednakże 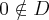 , zatem
, zatem  nie ma ekstremów lokalnych.
nie ma ekstremów lokalnych.
Przykład 3
Wyznaczymy ekstrema lokalne funkcji określonej wzorem 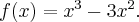
Zadanie rozpoczynamy od określenia dziedziny funkcji (w tym przypadku 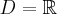 ) i zbadania, czy funkcja posiada punkty stacjonarne. Obliczamy pochodną funkcji
) i zbadania, czy funkcja posiada punkty stacjonarne. Obliczamy pochodną funkcji  :
:
Rozwiązujemy odpowiednie równanie:
Oba rozwiązania należą do dziedziny funkcji, a zatem  ma dwa punkty stacjonarne. Dalej rozstrzygamy o istnieniu ekstremów lokalnych w tych punktach stosując jedną z dwóch metod podanych poniżej.
ma dwa punkty stacjonarne. Dalej rozstrzygamy o istnieniu ekstremów lokalnych w tych punktach stosując jedną z dwóch metod podanych poniżej.
1 sposób (wykorzystujemy I warunek wystarczający istnienia ekstremum lokalnego)
Badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne:
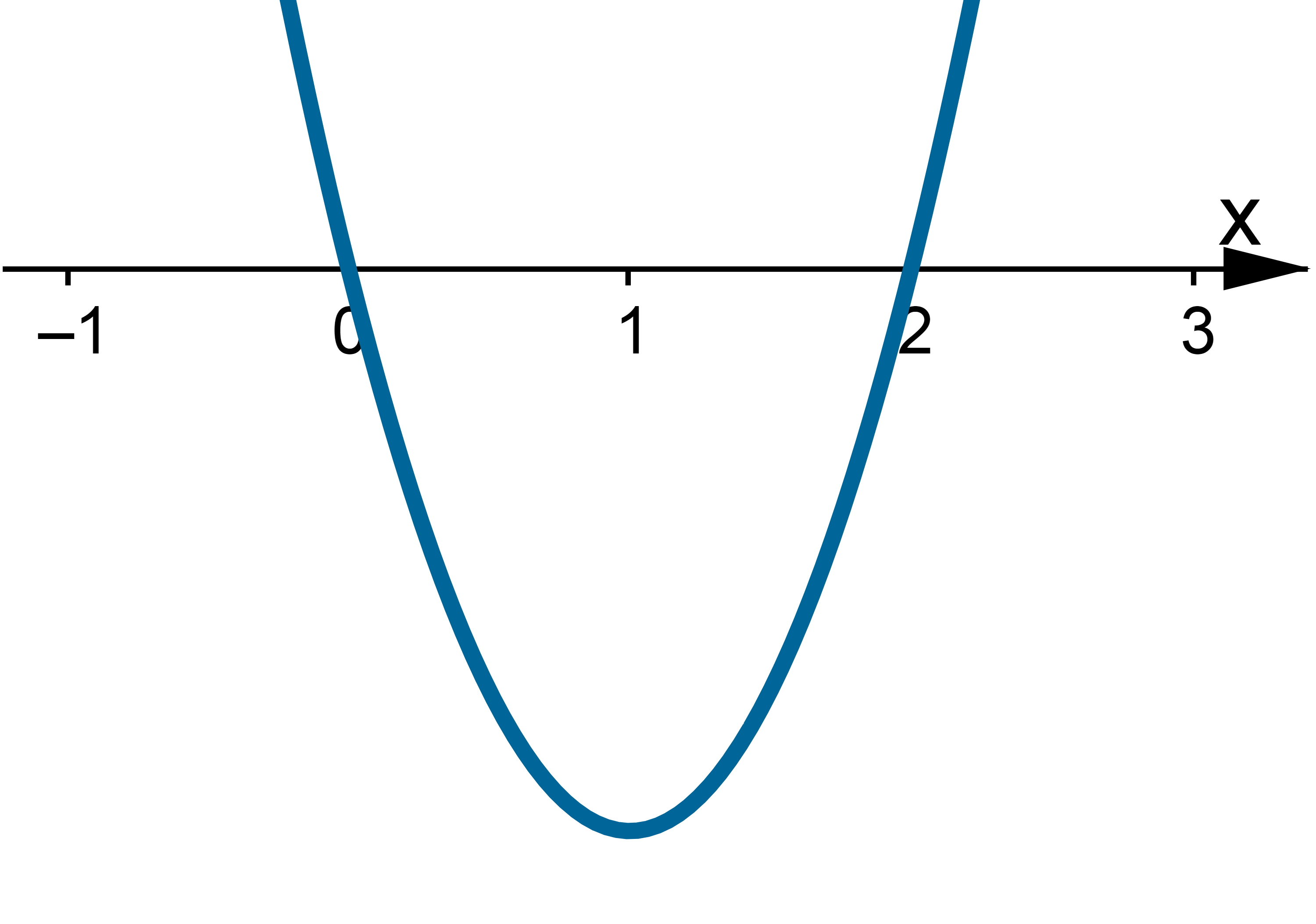 |
Stąd wynika, że 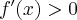 dla
dla 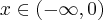 (a zatem także dla pewnego lewostronnego sąsiedztwa
(a zatem także dla pewnego lewostronnego sąsiedztwa  ) oraz
) oraz  dla
dla 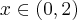 (przedział ten można potraktować jako prawostronne sąsiedztwo
(przedział ten można potraktować jako prawostronne sąsiedztwo  ). To oznacza, że
). To oznacza, że  ma w punkcie
ma w punkcie  maksimum lokalne
maksimum lokalne Pododnie
Pododnie  dla
dla 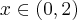 oraz
oraz 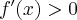 dla
dla 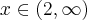 , czyli
, czyli  ma w punkcie
ma w punkcie  minimum lokalne.
minimum lokalne.
Metodę tę stosujemy najczęściej wtedy, gdy jednocześnie mamy wyznaczyć przedziały monotoniczności funkcji  .
.
2 sposób (wykorzystujemy II warunek wystarczający istnienia ekstremum lokalnego)
Obliczamy drugą pochodną funkcji  :
:
Ponieważ 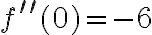 a zatem
a zatem  ma w punkcie
ma w punkcie  maksimum lokalne. Ponadto
maksimum lokalne. Ponadto 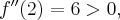 co oznacza, że
co oznacza, że  ma w punkcie
ma w punkcie  minimum lokalne.
minimum lokalne.
Ostatecznie stwierdzamy, że funkcja  posiada dwa ekstrema lokalne: maksimum lokalne w punkcie
posiada dwa ekstrema lokalne: maksimum lokalne w punkcie  o wartości
o wartości  oraz minimum lokalne w punkcie
oraz minimum lokalne w punkcie  o wartości
o wartości 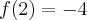 .
.
Przykład 4
Wyznaczymy ekstrema lokalne funkcji określonej wzorem 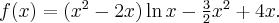
Funkcja  jest to przykładem funkcji, dla której szukając ekstremów lokalnych wygodniej jest stosować II warunek wystarczający.
jest to przykładem funkcji, dla której szukając ekstremów lokalnych wygodniej jest stosować II warunek wystarczający.
Dziedziną funkcji  jest zbiór
jest zbiór 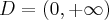 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  i zapisujemy ją w postaci iloczynowej:
i zapisujemy ją w postaci iloczynowej:
Wyznaczamy punkty stacjonarne funkcji  :
:
Dalej obliczamy drugą pochodną funkcji  :
:
Ponieważ
zatem  ma w punkcie
ma w punkcie 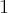 maksimum lokalne o wartości
maksimum lokalne o wartości 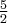 . Z kolei
. Z kolei
a zatem  ma w punkcie
ma w punkcie  minimum lokalne o wartości
minimum lokalne o wartości 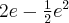 .
.
Przykład 5
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji określonej wzorem 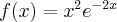 .
.
Na początek zauważmy, że 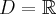 . Obliczamy pochodną funkcji i zapisujemy ją w postaci iloczynowej:
. Obliczamy pochodną funkcji i zapisujemy ją w postaci iloczynowej:
Wyznaczamy punkty stacjonarne funkcji  :
:
To oznacza, że funkcja  ma dwa punkty stacjonarne. Aby sprawdzić, czy
ma dwa punkty stacjonarne. Aby sprawdzić, czy  ma w nich ekstrema lokalne, zastosujemy I warunek wystarczający istnienia ekstremum lokalnego. W tym celu badamy, gdzie pochodna funkcji
ma w nich ekstrema lokalne, zastosujemy I warunek wystarczający istnienia ekstremum lokalnego. W tym celu badamy, gdzie pochodna funkcji  przyjmuje wartości dodatnie, a gdzie ujemne:
przyjmuje wartości dodatnie, a gdzie ujemne:
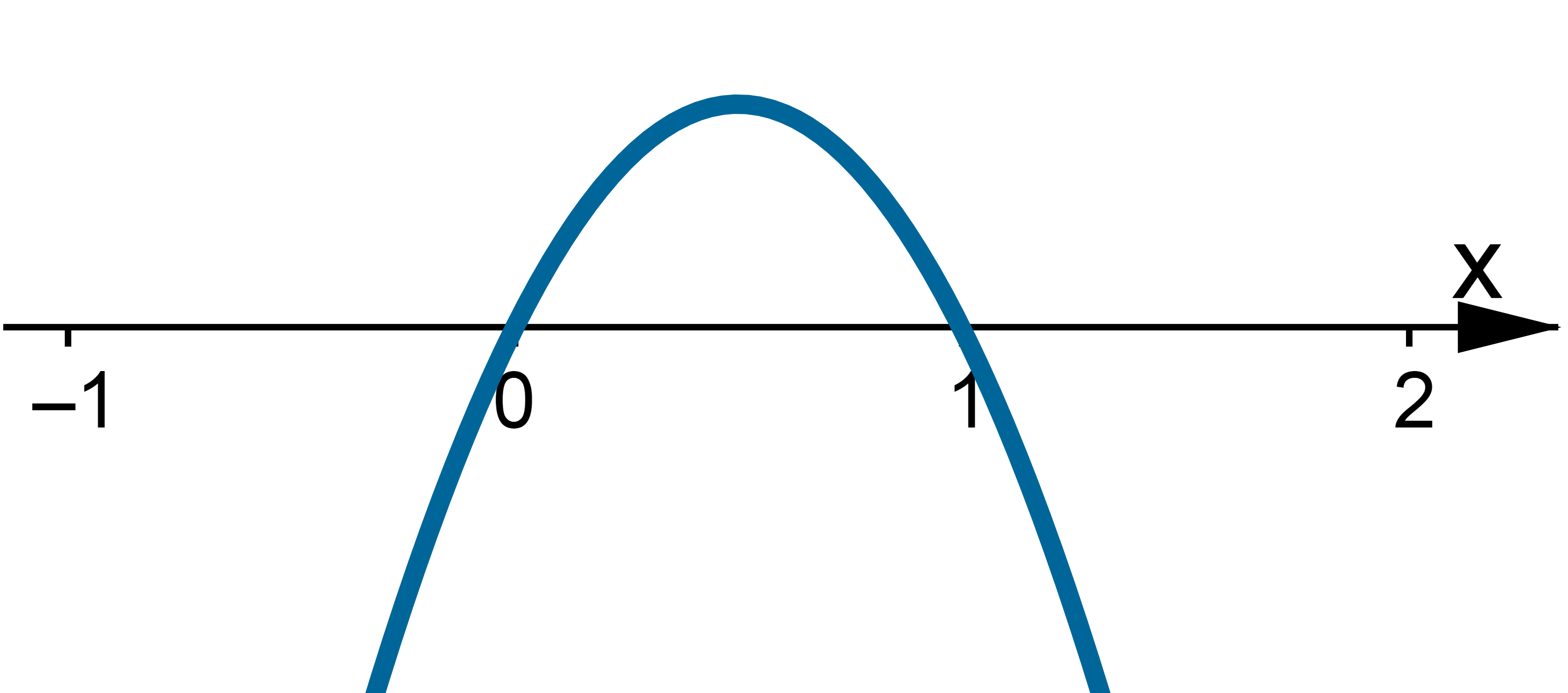
Stąd wynika, że istnieją sąsiedztwa 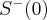 i
i 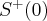 takie, że
takie, że 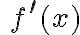 dla
dla 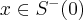 oraz
oraz 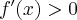 dla
dla 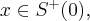 czyli
czyli  ma w
ma w  minimum lokalne. Podobnie uzasadniamy, że w
minimum lokalne. Podobnie uzasadniamy, że w 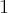 istnieje maksimum lokalne.
istnieje maksimum lokalne.
Uzyskane wyniki i odpowiedź (uwzględniając również przedziały monotoniczności badanej funkcji) najczęściej zapisujemy w postaci tabeli.
 |
 |
 |
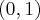 |
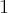 |
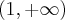 |
 |
 |
 |
 |
 |
 |
 |
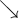 |
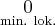 |
 |
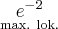 |
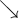 |


Przykład 6
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji określonej wzorem 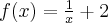 arctg
arctg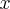 .
.
Na początek zauważmy, że 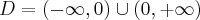 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
Wyznaczamy punkty stacjonarne funkcji  :
:
Następnie badamy, gdzie pochodna funkcji  przyjmuje wartości dodatnie, a gdzie ujemne:
przyjmuje wartości dodatnie, a gdzie ujemne:
więc ostatecznie
Analogicznie
Uzyskane wyniki zapisujemy w tabeli:
 |
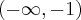 |
 |
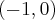 |
 |
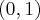 |
 |
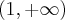 |
|
 |
 |
 |
 |
X |  |
 |
 |
|
 |
 |
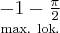 |
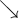 |
X | 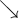 |
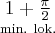 |
 |
Przykład 7
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji określonej wzorem 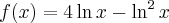 .
.
Na początek zauważmy, że 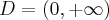 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
Wyznaczamy punkty stacjonarne funkcji  :
:
Jeśli 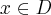 , to mianownik pierwszej pochodnej jest dodatni, a zatem
, to mianownik pierwszej pochodnej jest dodatni, a zatem
Analogicznie
Uzyskane wyniki zapisujemy w tabeli:
 |
 |
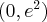 |
 |
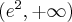 |
|
 |
X |  |
 |
 |
|
 |
X |  |
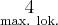 |
 |
Przykład 8
Wyznaczymy ekstrema lokalne i przedziały monotoniczności funkcji określonej wzorem 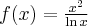 . Następnie naszkicujemy wykres funkcji
. Następnie naszkicujemy wykres funkcji  wiedząc dodatkowo, że
wiedząc dodatkowo, że 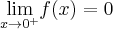 ,
, 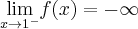 ,
, 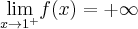 oraz
oraz 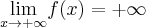 .
.
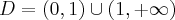 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
Wyznaczamy punkty stacjonarne funkcji  :
:
Uzyskane wyniki zapisujemy w tabeli:
 |
0 | 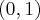 |
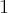 |
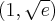 |
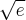 |
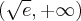 |
|
 |
X |  |
X |  |
 |
 |
|
 |
X | 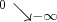 |
X | 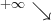 |
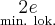 |
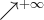 |
Na podstawie uzyskanych informacji szkicujemy wykres funkcji  :
:
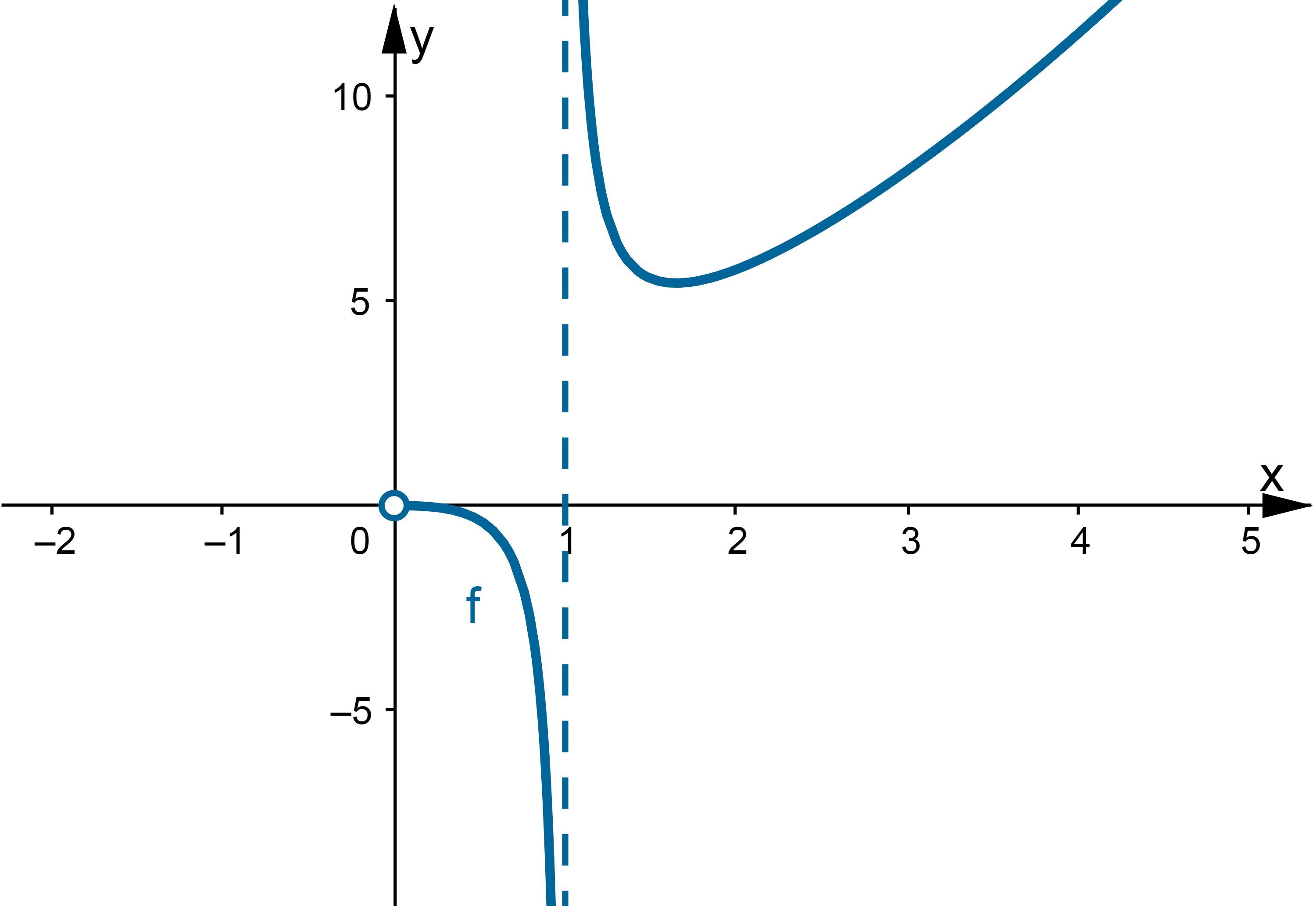
Teoria
Definicja. Załóżmy, że funkcja  jest określona na pewnym otoczeniu
jest określona na pewnym otoczeniu  punktu
punktu  . Mówimy, że
. Mówimy, że  ma w punkcie
ma w punkcie  maksimum lokalne, jeżeli istnieje otoczenie
maksimum lokalne, jeżeli istnieje otoczenie  , punktu
, punktu  , takie, że dla wszystkich
, takie, że dla wszystkich 
Definicja. Załóżmy, że funkcja  jest określona na pewnym otoczeniu
jest określona na pewnym otoczeniu  punktu
punktu  . Mówimy, że
. Mówimy, że  ma w punkcie
ma w punkcie  minimum lokalne, jeżeli istnieje otoczenie
minimum lokalne, jeżeli istnieje otoczenie  , punktu
, punktu  , takie, że dla wszystkich
, takie, że dla wszystkich 
Uwaga. Jeżeli dla każdego 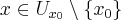 zachodzi nierówność
zachodzi nierówność 
 , to mówimy o maksimum (minimum) lokalnym właściwym.
, to mówimy o maksimum (minimum) lokalnym właściwym.
Twierdzenie - warunek konieczny istnienia ekstremum lokalnego dla funkcji różniczkowalnej. Jeżeli funkcja  jest różniczkowalna w punkcie
jest różniczkowalna w punkcie  i ma w tym punkcie ekstremum lokalne, to
i ma w tym punkcie ekstremum lokalne, to 
Uwaga. Jeżeli  , to funkcja
, to funkcja  nie ma ekstremum w punkcie
nie ma ekstremum w punkcie  .
.
Uwaga. Funkcja może mieć ekstremum lokalne jedynie w punkcie  , takim że
, takim że  (gdy jest różniczkowalna w
(gdy jest różniczkowalna w  ) lub w punkcie
) lub w punkcie  , w którym funkcja
, w którym funkcja  nie ma pochodnej.
nie ma pochodnej.
Definicja. Punkty, w których pochodna funkcji się zeruje nazywamy punktami stacjonarnymi tej funkcji.
Twierdzenie - warunek wystarczający istnienia ekstremum lokalnego. Jeżeli funkcja  jest ciągła na pewnym otoczeniu
jest ciągła na pewnym otoczeniu  i różniczkowalna na sąsiedztwie
i różniczkowalna na sąsiedztwie  punktu
punktu  oraz
oraz
lub
to funkcja  ma w punkcie
ma w punkcie  ekstremum lokalne właściwe. Jest to maksimum lokalne w przypadku (1), minimum lokalne gdy zachodzi warunek (2).
ekstremum lokalne właściwe. Jest to maksimum lokalne w przypadku (1), minimum lokalne gdy zachodzi warunek (2).
Twierdzenie - drugi warunek wystarczający istnienia ekstremum lokalnego. Jeżeli funkcja  jest dwukrotnie różniczkowalna na pewnym otoczeniu punktu
jest dwukrotnie różniczkowalna na pewnym otoczeniu punktu  oraz
oraz
to funkcja  ma w punkcie
ma w punkcie  ekstremum lokalne właściwe, przy czym jest to maksimum lokalne,
ekstremum lokalne właściwe, przy czym jest to maksimum lokalne,
jeżeli  , minimum lokalne, gdy
, minimum lokalne, gdy  .
.
Ćwiczenia interaktywne
Przyporządkuj podane funkcje do odpowiedniej grupy.
Ćwiczenie 1
Jeśli ![f:[-3,3] \to \mathbb{R} f:[-3,3] \to \mathbb{R}](https://port.edu.p.lodz.pl/filter/tex/pix.php/e142a1e589322ea820313a5c589f7bc5.png) jest funkcją, której wykres przedstawia poniższy rysunek, to
jest funkcją, której wykres przedstawia poniższy rysunek, to
Ćwiczenie 2
Przyporządkuj podane funkcje do odpowiedniej grupy.
...
Ćwiczenie 1a
Ćwiczenie 1b
Ćwiczenie 3
Uzupełnij przeciągając poprawne odpowiedzi.
Z informacji zawartych w powyższej tabeli wynika, że
Ćwiczenie 4
Wybrane informacje o pierwszej i drugiej pochodnej pewnej dwukrotnie różniczkowalnej funkcji 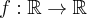 zawarte są w poniższej tabeli. Uzupełnij trzeci wiersz tabeli.
zawarte są w poniższej tabeli. Uzupełnij trzeci wiersz tabeli.
Zawartość pustych pól w tabeli możesz zmienić poprzez kliknięcie.
Ćwiczenie 5
Czy funkcja  posiada ekstrema lokalne we wskazanych punktach? Uzasadnij odpowiedź.
posiada ekstrema lokalne we wskazanych punktach? Uzasadnij odpowiedź.
Ćwiczenia interaktywne, cz.2
Ćwiczenie 6
Niech 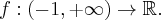 Informacje o pierwszej pochodnej funkcji
Informacje o pierwszej pochodnej funkcji  zawarte są w poniższej tabeli. Uzupełnij trzeci wiersz tabeli.
zawarte są w poniższej tabeli. Uzupełnij trzeci wiersz tabeli.
Zawartość pustych pól w tabeli możesz zmienić poprzez kliknięcie.
Te rysunki mogą przedstawiać wykres funkcji  :
:
Ćwiczenie 7
Niech 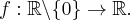 Informacje o pierwszej pochodnej funkcji
Informacje o pierwszej pochodnej funkcji  zawarte są w poniższej tabeli. Uzupełnij trzeci wiersz tabeli.
zawarte są w poniższej tabeli. Uzupełnij trzeci wiersz tabeli.
Zawartość pustych pól w tabeli możesz zmienić poprzez kliknięcie.
3.3 Ekstrema globalne funkcji
...
Teoria
...
Przykłady
...
Ćwiczenia interaktywne
...
3.4 Zadania
Zadanie 1
Wyznacz ekstrema lokalne i przedziały monotoniczności funkcji określonej wzorem:
Odpowiedź: Dziedziną funkcji jest zbiór 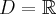 . Funkcja jest rosnąca w każdym z przedziałów:
. Funkcja jest rosnąca w każdym z przedziałów:  ,
, 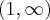 , malejąca w przedziale
, malejąca w przedziale 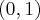 , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne,  , w punkcie
, w punkcie 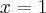 funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 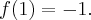
Odpowiedź: Dziedziną funkcji jest zbiór 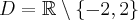 . Funkcja jest rosnąca w każdym z przedziałów:
. Funkcja jest rosnąca w każdym z przedziałów: 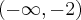 ,
, 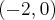 , malejąca w każdym z przedziałów:
, malejąca w każdym z przedziałów: 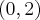 ,
, 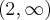 w punkcie
w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 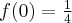 .
.
Funkcja jest rosnąca w każdym z przedziałów: 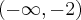 ,
, 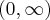 ,
,
malejąca w przedziale 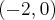 , w punkcie
, w punkcie  funkcja ma minimum lokalne, o wartości
funkcja ma minimum lokalne, o wartości  , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 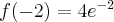 .
.
Odpowiedź: Dziedziną funkcji jest zbiór 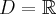 . Funkcja jest rosnąca w całej swojej dziedzinie.
. Funkcja jest rosnąca w całej swojej dziedzinie.
Odpowiedź: Dziedziną funkcji jest zbiór 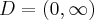 . Funkcja jest rosnąca w przedziale
. Funkcja jest rosnąca w przedziale 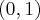 , malejąca w przedziale
, malejąca w przedziale 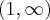 , w punkcie
, w punkcie 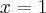 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 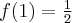 .
.
Odpowiedź: Dziedziną funkcji jest zbiór 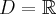 . Funkcja jest rosnąca w każdym z przedziałów:
. Funkcja jest rosnąca w każdym z przedziałów: 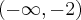 ,
, 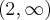 , malejąca w przedziale
, malejąca w przedziale 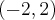 , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 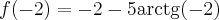 , w punkcie
, w punkcie  funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 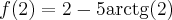 .
.
Odpowiedź: Dziedziną funkcji jest zbiór 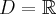 . Funkcja jest malejąca w każdym z przedziałów:
. Funkcja jest malejąca w każdym z przedziałów: 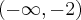 ,
,
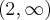 , rosnąca w przedziale
, rosnąca w przedziale 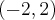 , w punkcie
, w punkcie  funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 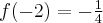 , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 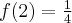 .
.
Odpowiedź: Dziedziną funkcji jest zbiór 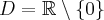 . Funkcja jest rosnąca w każdym z przedziałów:
. Funkcja jest rosnąca w każdym z przedziałów:  ,
, 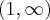 , malejąca w przedziale
, malejąca w przedziale 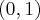 , w punkcie
, w punkcie 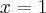 funkcja ma minimum lokalne,
funkcja ma minimum lokalne,  .
.
Odpowiedź: Dziedziną funkcji jest zbiór 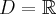 . Funkcja jest rosnąca w każdym z przedziałów:
. Funkcja jest rosnąca w każdym z przedziałów:  ,
, 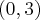 , malejąca w przedziale
, malejąca w przedziale 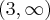 , w punkcie j
, w punkcie j 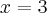 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 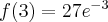 .
.
Odpowiedź: Dziedziną funkcji jest zbiór 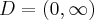 . Funkcja jest rosnąca w przedziale
. Funkcja jest rosnąca w przedziale 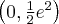 , malejąca w przedziale
, malejąca w przedziale 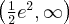 , w punkcie
, w punkcie 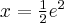 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 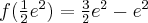 .
.
Odpowiedź: Dziedziną funkcji jest zbiór 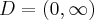 . Funkcja jest rosnąca w każdym z przedziałów:
. Funkcja jest rosnąca w każdym z przedziałów: 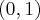 ,
, 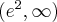 , malejąca w przedziale
, malejąca w przedziale 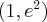 , w punkcie
, w punkcie 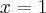 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 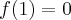 , w punkcie
, w punkcie 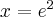 funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 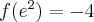 .
.
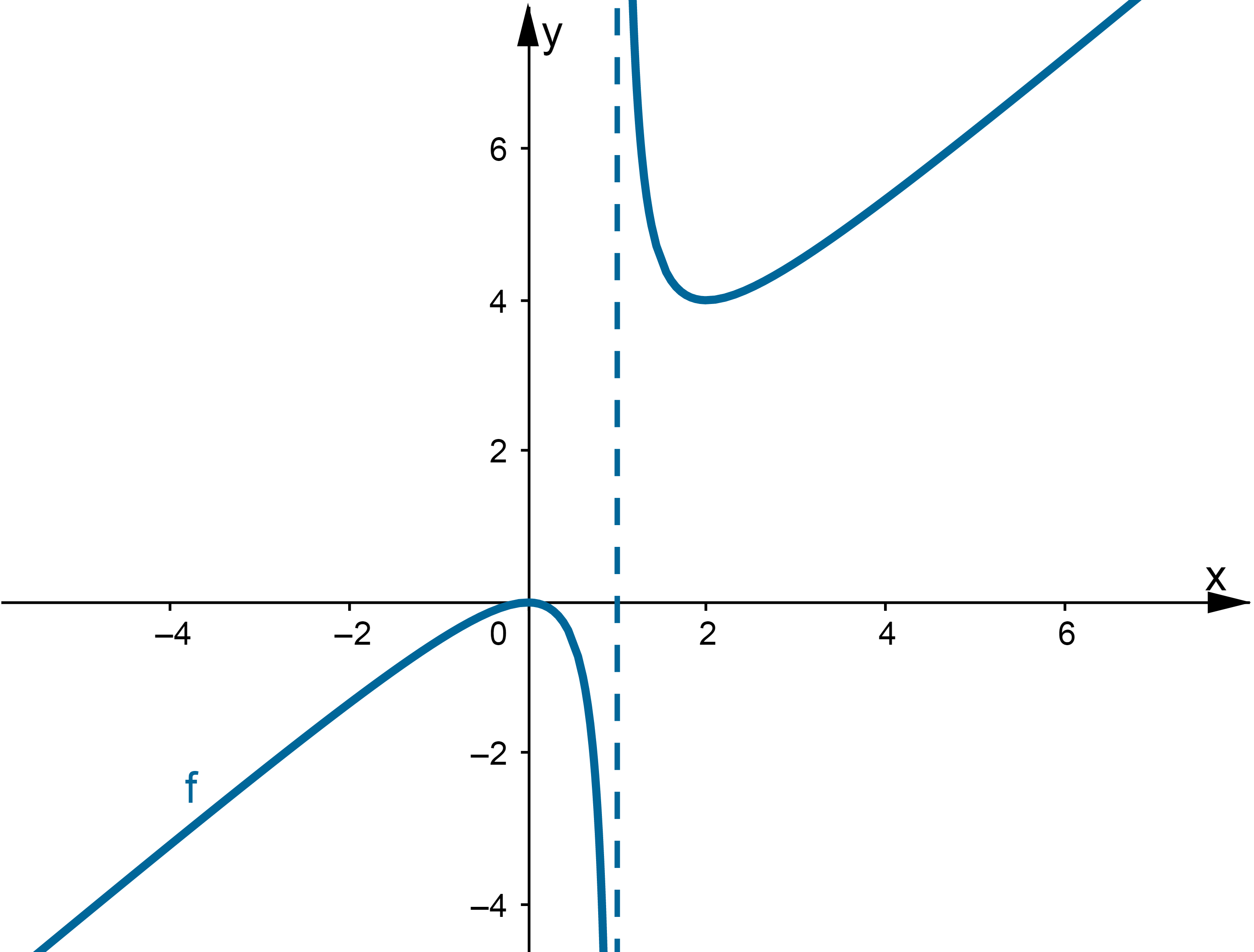
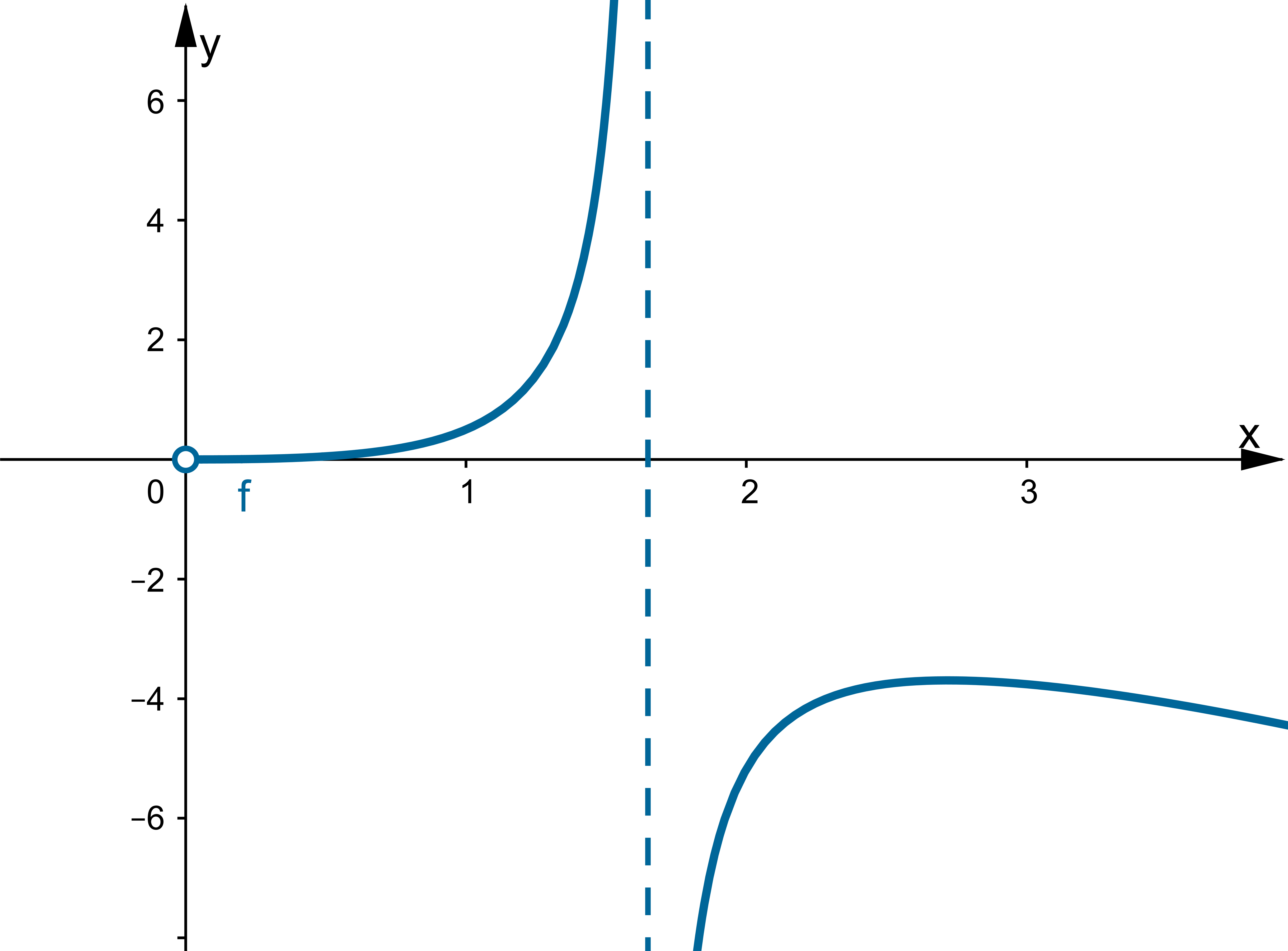
Zadanie 2
Wyznacz asymptoty, ekstrema lokalne, przedziały monotoniczności oraz naszkicuj wykres funkcji określonej wzorem:
Wskazówka: Asymptotę pionową wykres funkcji  może posiadać w punkcie
może posiadać w punkcie 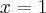 , ukośną w
, ukośną w 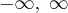 ,
, 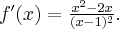
Odpowiedź: Dziedziną funkcji jest zbiór 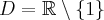 . Funkcja ma asymptotę pionową obustronną
. Funkcja ma asymptotę pionową obustronną 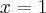 , asymptotę ukośną
, asymptotę ukośną 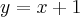 w
w 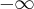 i w
i w 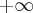 . Funkcja jest malejąca w każdym z przedziałów:
. Funkcja jest malejąca w każdym z przedziałów: 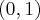 ,
, 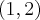 , rosnąca w każdym z przedziałów:
, rosnąca w każdym z przedziałów:  ,
, 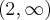 , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne,  , w punkcie
, w punkcie  funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 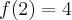 .
.
Wskazówka: Asymptotę ukośną wykres funkcji  może posiadać w
może posiadać w 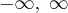 , asymptoty pionowej wykres funkcji
, asymptoty pionowej wykres funkcji  nie posiada.
nie posiada.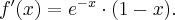
Odpowiedź: Dziedziną funkcji jest zbiór 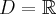 . Funkcja ma asymptotę poziomą
. Funkcja ma asymptotę poziomą 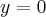 w
w 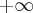 . Funkcja jest rosnąca w przedziale
. Funkcja jest rosnąca w przedziale 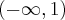 , malejąca w przedziale
, malejąca w przedziale 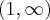 , w punkcie
, w punkcie 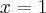 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 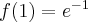 .
.
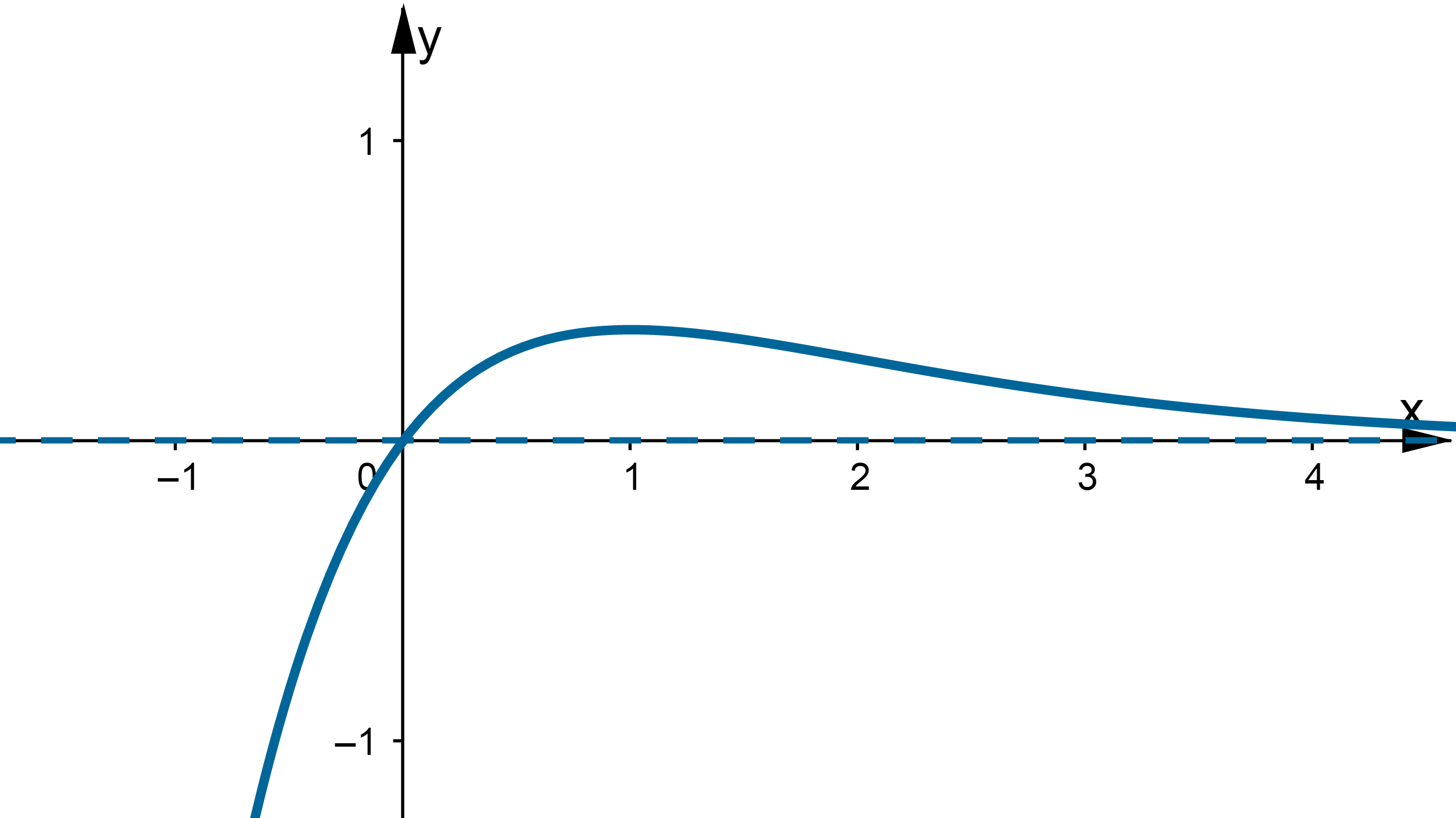
Wskazówka: Asymptotę pionową wykres funkcji może posiadać w punktach:
 ,
, 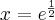 , asyptotę ukośną wykres funkcji może posiadać w
, asyptotę ukośną wykres funkcji może posiadać w 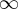 .
. 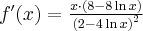 .
.
Odpowiedź: Dziedziną funkcji jest zbiór 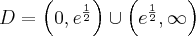 .
.
Funkcja ma asymptotę pionową obustronną 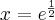 .
.
Funkcja jest rosnąca w każdym z przedziałów 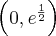 ,
,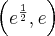 , malejąca w przedziale
, malejąca w przedziale 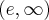 ,
,
w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 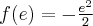 .
.
4. Wypukłość, wklęsłość funkcji, punkty przegięcia
,,,
4.1 Punkty przegięcia wykresu funkcji
...
Teoria
...
Przykłady
...
Ćwiczenia interaktywne
Ćwiczenie 2
Przyporządkuj podane funkcje do odpowiedniej grupy.
...
4.2 Badanie wklęsłości i wypukłości wykresu funkcji
...
Teoria
...
Przykłady
...
Ćwiczenia interaktywne
Ćwiczenie 0
Dokończ poprawnie zdanie wybierając jedną z odpowiedzi.
Zobacz podpowiedź:
Ćwiczenie 1
Zastanów się, które rysunki przedstawiają wykresy funkcji wypukłej/wklęsłej na poszczególnych przedziałach dziedziny.
Ćwiczenie 2
Dokończ zdanie wybierając poprawne odpowiedzi.
Ćwiczenie 3
Uzupełnij luki.
Ćwiczenie 4
Druga pochodna funkcji 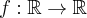 dana jest wzorem
dana jest wzorem 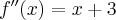 .
.
Ćwiczenie 4a
Dany jest wykres drugiej pochodnej funkcji 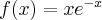 . Dopasuj własności: wypukła/wklęsła do poszczególnych fragmentów wykresu.
. Dopasuj własności: wypukła/wklęsła do poszczególnych fragmentów wykresu.
Ćwiczenie 4b
Druga pochodna funkcji 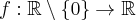 jest dodatnia dla
jest dodatnia dla 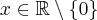 . Zastanów się, czy funkcja może mieć wykres przedstawiony poniżej.
. Zastanów się, czy funkcja może mieć wykres przedstawiony poniżej.
Ćwiczenie 4c
Druga pochodna funkcji  jest ujemna w całej dziedzinie. Zastanów się, czy funkcja może mieć wykres przedstawiony poniżej.
jest ujemna w całej dziedzinie. Zastanów się, czy funkcja może mieć wykres przedstawiony poniżej.
Ćwiczenie 5
Wiedząc, że funkcja  jest różniczkowalna w punkcie
jest różniczkowalna w punkcie  , uzupełnij trzeci wiersz tabeli.
, uzupełnij trzeci wiersz tabeli.
Zawartość pustych pól w tabeli możesz zmienić poprzez kliknięcie.
Ćwiczenie 6
Wybrane informacje o drugiej pochodnej pewnej funkcji 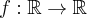 zawarte są w poniższej tabeli.
zawarte są w poniższej tabeli.
Wybierz rysunki mogące przedstawiać wykres funkcji  .
.
Przenieś wybrane rysunki do obszaru znajdującego się nad nimi.
Ćwiczenie 7
Wybrane informacje o drugiej pochodnej pewnej dwukrotnie różniczkowalnej funkcji 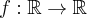 zawarte są w poniższej tabeli. Uzupełnij trzeci wiersz tabeli.
zawarte są w poniższej tabeli. Uzupełnij trzeci wiersz tabeli.
Zawartość pustych pól w tabeli możesz zmienić poprzez kliknięcie.
4.3 Zadania
...
5. Badanie przebiegu zmienności funkcji
...
Teoria
...
Przykłady
Przykład 4
Stół bilardowy ma następujący kształt (bandy są w kształcie parabol). Gracz ma
możliwość ustawienia bili w dowolnym miejscu na linii łączącej wierzchołki parabol. Jego zadanie polega na traeniu do pokazanego otworu przy wykorzystaniu dokładnie jednego odbicia od bandy. Zakładając, że ustawił bilę w konkretnym miejscu, w którym kierunku powinien uderzyć?
Przykład 5
z zerami
bez zer
Ćwiczenia interaktywne
Ćwiczenie 2
Oblicz podane granice.
Uzupełnij puste pola.
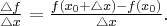
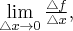
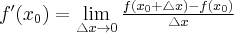
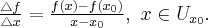
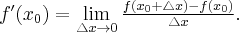
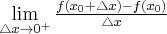
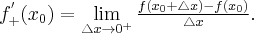
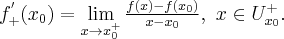
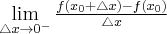
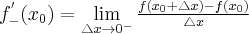
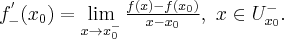
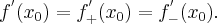
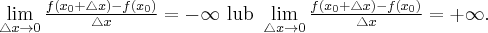
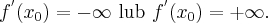
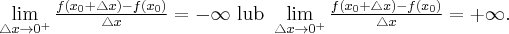
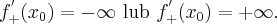
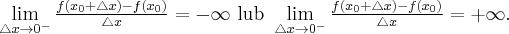
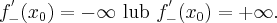
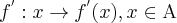
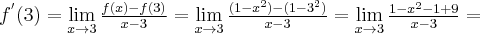
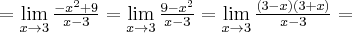
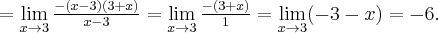
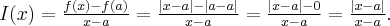
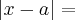
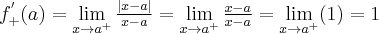
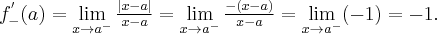
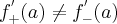
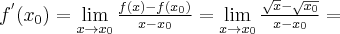
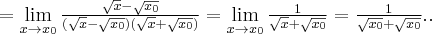
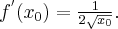
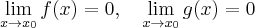
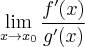


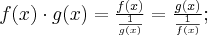

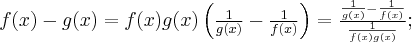





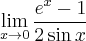
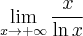
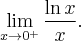

![\dfrac{e^x-1}{2\sin x} = \left[\dfrac{0}{0}\right] \dfrac{e^x-1}{2\sin x} = \left[\dfrac{0}{0}\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/3a32e8a400e82e6025c8fc27f796d3e7.png)



![\underset{x\rightarrow +\infty }{\lim }\, \dfrac{x}{\ln x} = \left[\dfrac{\infty}{\infty}\right] \overset{\text{H}}{=} \underset{x\rightarrow +\infty }{\lim }\, \dfrac{x}{\ln x} = \left[\dfrac{\infty}{\infty}\right] \overset{\text{H}}{=}](https://port.edu.p.lodz.pl/filter/tex/pix.php/f51b93dc00924ac3be8ae55eb4aec36b.png)
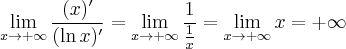
![\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\ln x }{x} = \left[\dfrac{-\infty}{0^{+}}\right]. \underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\ln x }{x} = \left[\dfrac{-\infty}{0^{+}}\right].](https://port.edu.p.lodz.pl/filter/tex/pix.php/d8ff9a271b17743a4c7cfd0f3a66f70e.png)
![\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\ln x }{x} = \underset{x\rightarrow 0^{+} }{\lim }\, \ln x \cdot \dfrac{1}{x} =\left[-\infty \cdot \dfrac{1}{0^{+}}\right] = [-\infty \cdot \infty]=-\infty. \underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\ln x }{x} = \underset{x\rightarrow 0^{+} }{\lim }\, \ln x \cdot \dfrac{1}{x} =\left[-\infty \cdot \dfrac{1}{0^{+}}\right] = [-\infty \cdot \infty]=-\infty.](https://port.edu.p.lodz.pl/filter/tex/pix.php/d9c9c4343188476654c6443e78e3ba90.png)
![\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{(\ln x)'}{(x)'} =\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\frac{1}{x}}{1} = \left[\dfrac{1}{0^{+}}\right] = +\infty , \underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{(\ln x)'}{(x)'} =\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\frac{1}{x}}{1} = \left[\dfrac{1}{0^{+}}\right] = +\infty ,](https://port.edu.p.lodz.pl/filter/tex/pix.php/bbb5e72bdead71840570c10cc44b91cf.png)
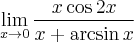
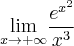
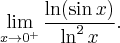
![\underset{x\rightarrow 0}{\lim }\,\dfrac{x\cos 2x}{x+\arcsin x} = \left[\dfrac{0}{0}\right]\overset{\text{H}}{=} \underset{x\rightarrow 0}{\lim }\dfrac{(x\cos 2x)'}{(x+\arcsin x)'}=\underset{x\rightarrow 0}{\lim }\,\dfrac{\cos 2x-x\sin 2x\cdot 2}{1+\frac{1}{\sqrt{1-x^{2}}}}= \underset{x\rightarrow 0}{\lim }\,\dfrac{x\cos 2x}{x+\arcsin x} = \left[\dfrac{0}{0}\right]\overset{\text{H}}{=} \underset{x\rightarrow 0}{\lim }\dfrac{(x\cos 2x)'}{(x+\arcsin x)'}=\underset{x\rightarrow 0}{\lim }\,\dfrac{\cos 2x-x\sin 2x\cdot 2}{1+\frac{1}{\sqrt{1-x^{2}}}}=](https://port.edu.p.lodz.pl/filter/tex/pix.php/10b4959c1038fb647798ed685676c5a1.png)
![\left[\dfrac{1-0}{1+1}\right]=\dfrac{1}{2}\,. \left[\dfrac{1-0}{1+1}\right]=\dfrac{1}{2}\,.](https://port.edu.p.lodz.pl/filter/tex/pix.php/14781e69ee53cceba5f856da788ecd37.png)
![\underset{x\rightarrow + \infty }{\lim }\dfrac{e^{x^{2}}}{x^{3}}=\left[ \dfrac{\infty }{\infty }\right] \overset{\text{H}}{=}\underset{x\rightarrow +\infty } {\lim }\dfrac{(e^{x^{2}})^{\prime }}{(x^{3})^{\prime }}=\underset{ x\rightarrow +\infty }{\lim }\dfrac{e^{x^{2}}\cdot 2x}{3x^{2}}=\underset{ x\rightarrow +\infty }{\lim }\dfrac{2e^{x^{2}}}{3x}=\left[ \dfrac{\infty }{\infty }\right] \overset{\text{H}}{=} \underset{x\rightarrow + \infty }{\lim }\dfrac{e^{x^{2}}}{x^{3}}=\left[ \dfrac{\infty }{\infty }\right] \overset{\text{H}}{=}\underset{x\rightarrow +\infty } {\lim }\dfrac{(e^{x^{2}})^{\prime }}{(x^{3})^{\prime }}=\underset{ x\rightarrow +\infty }{\lim }\dfrac{e^{x^{2}}\cdot 2x}{3x^{2}}=\underset{ x\rightarrow +\infty }{\lim }\dfrac{2e^{x^{2}}}{3x}=\left[ \dfrac{\infty }{\infty }\right] \overset{\text{H}}{=}](https://port.edu.p.lodz.pl/filter/tex/pix.php/5b80619ac8676c4a800681bf3a57b9d2.png)
![=\underset{ x\rightarrow +\infty }{\lim }\dfrac{(2e^{x^{2}})^{\prime }}{(3x)^{\prime }}=\underset{x\rightarrow +\infty }{\lim }\dfrac{2e^{x^{2}}\cdot 2x}{3 }=\left[ \dfrac{\infty}{3} \right] =\infty . =\underset{ x\rightarrow +\infty }{\lim }\dfrac{(2e^{x^{2}})^{\prime }}{(3x)^{\prime }}=\underset{x\rightarrow +\infty }{\lim }\dfrac{2e^{x^{2}}\cdot 2x}{3 }=\left[ \dfrac{\infty}{3} \right] =\infty .](https://port.edu.p.lodz.pl/filter/tex/pix.php/0287e8713487754bc8128c0558c0d206.png)
![\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{\ln (\sin x )}{\ln ^{2}{x}}=\left[ \dfrac{-\infty }{\infty }\right] \overset{\text{H}}{=}\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{\frac{1}{\sin x}\cdot \cos x}{2\ln x \cdot \frac{1}{x}}=\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{x}{\sin x} \cdot \dfrac{\cos x}{2\ln x}=\left[ 1\cdot\dfrac{1}{-\infty}\right] =0 \underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{\ln (\sin x )}{\ln ^{2}{x}}=\left[ \dfrac{-\infty }{\infty }\right] \overset{\text{H}}{=}\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{\frac{1}{\sin x}\cdot \cos x}{2\ln x \cdot \frac{1}{x}}=\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{x}{\sin x} \cdot \dfrac{\cos x}{2\ln x}=\left[ 1\cdot\dfrac{1}{-\infty}\right] =0](https://port.edu.p.lodz.pl/filter/tex/pix.php/d561fe251231a59d20bc3ef61fef5c00.png)
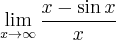
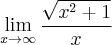
![\underset{x\rightarrow +\infty }{\lim }\, \dfrac{x-\sin x }{x} = \left[\dfrac{\infty}{\infty}\right], \underset{x\rightarrow +\infty }{\lim }\, \dfrac{x-\sin x }{x} = \left[\dfrac{\infty}{\infty}\right],](https://port.edu.p.lodz.pl/filter/tex/pix.php/1fce53623ff80629e513e56fdaaa02ee.png)
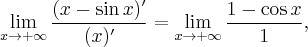
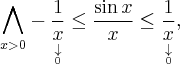
![\underset{x\rightarrow +\infty }{\lim }\dfrac{x-\sin x }{x}=\underset{x\rightarrow +\infty }{\lim }\left(1-\dfrac{\sin x}{x} \right)=[1-0]=1. \underset{x\rightarrow +\infty }{\lim }\dfrac{x-\sin x }{x}=\underset{x\rightarrow +\infty }{\lim }\left(1-\dfrac{\sin x}{x} \right)=[1-0]=1.](https://port.edu.p.lodz.pl/filter/tex/pix.php/8d0df21e7261733e76d66d0d045c8cca.png)
![\underset{x\rightarrow \infty}{\lim }\,\dfrac{\sqrt{x^2+1}}{x}=\left[\dfrac{\infty}{\infty}\right]\overset{\text{H}}{=}\underset{x\rightarrow \infty}{\lim }\,\dfrac{\frac{1}{2\sqrt{x^2+1}}\cdot 2x}{1}=\underset{x\rightarrow \infty}{\lim }\,\dfrac{x}{\sqrt{x^2+1}}\overset{\text{H}}{=}\underset{x\rightarrow \infty}{\lim }\,\dfrac{\sqrt{x^2+1}}{x}, \underset{x\rightarrow \infty}{\lim }\,\dfrac{\sqrt{x^2+1}}{x}=\left[\dfrac{\infty}{\infty}\right]\overset{\text{H}}{=}\underset{x\rightarrow \infty}{\lim }\,\dfrac{\frac{1}{2\sqrt{x^2+1}}\cdot 2x}{1}=\underset{x\rightarrow \infty}{\lim }\,\dfrac{x}{\sqrt{x^2+1}}\overset{\text{H}}{=}\underset{x\rightarrow \infty}{\lim }\,\dfrac{\sqrt{x^2+1}}{x},](https://port.edu.p.lodz.pl/filter/tex/pix.php/74c72acd6e48e1e5fecae1f74178c6ab.png)