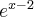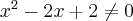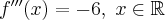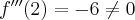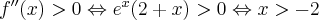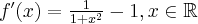5.2 Punkty przegięcia wykresu funkcji
Przykłady
Dziedziną funkcji jest zbiór  .
.
Obliczamy pierwszą i drugą pochodną funkcji  :
:
Zauważmy, że dla każdego  pochodna rzędu drugiego jest dodatnia, zatem nie jest spełniony warunek konieczny istnienia punktu przegięcia i wykres funkcji
pochodna rzędu drugiego jest dodatnia, zatem nie jest spełniony warunek konieczny istnienia punktu przegięcia i wykres funkcji  nie posiada punktów przegięcia.
nie posiada punktów przegięcia.
Funkcja  jest wielomianem, jest więc określona dla każdego
jest wielomianem, jest więc określona dla każdego  .
.
Obliczamy pierwszą i drugą pochodną funkcji  :
:
i przyrównujemy drugą pochodną do zera:
Stąd wynika, że wykres funkcji  może mieć tylko jeden punkt przegięcia. Dalej o istnieniu punktu przegięcia rozstrzygamy stosując jedną z dwóch metod podanych poniżej.
może mieć tylko jeden punkt przegięcia. Dalej o istnieniu punktu przegięcia rozstrzygamy stosując jedną z dwóch metod podanych poniżej.
1 sposób (wykorzystamy I warunek wystarczający istnienia punktu przegięcia)
Badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie a gdzie ujemne:
oraz
Stąd wynika, że  dla
dla 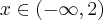 (a zatem także dla pewnego lewostronnego sąsiedztwa 2) oraz
(a zatem także dla pewnego lewostronnego sąsiedztwa 2) oraz  dla
dla  (przedział ten można potraktować jako prawostronne sąsiedztwo 2). Zatem punkt
(przedział ten można potraktować jako prawostronne sąsiedztwo 2). Zatem punkt  jest punktem przegięcia wykresu funkcji
jest punktem przegięcia wykresu funkcji  .
.
Metodę tę stosujemy najczęściej wtedy, gdy jednocześnie mamy wyznaczyć przedziały wklęsłości i wypukłości funkcji  .
.
2 sposób (wykorzystamy II warunek wystarczający istnienia punktu przegięcia)
Funkcja  jest określona dla każdego
jest określona dla każdego  .
.
Obliczamy pierwszą i drugą pochodną funkcji  :
:
i przyrównujemy drugą pochodną do zera:
Ponieważ  dla każdego
dla każdego  , więc
, więc  dla
dla  . Oczywiście
. Oczywiście  należy do dziedziny funkcji. Dalej badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie a gdzie ujemne:
należy do dziedziny funkcji. Dalej badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie a gdzie ujemne:
oraz
Ponieważ  dla
dla  , więc funkcja jest wypukła na przedziale
, więc funkcja jest wypukła na przedziale  . Ponieważ
. Ponieważ  dla
dla  , więc funkcja jest wklęsła na przedziale
, więc funkcja jest wklęsła na przedziale 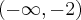 . Na mocy I warunku wystarczającego istnienia punktu przegięcia punkt
. Na mocy I warunku wystarczającego istnienia punktu przegięcia punkt  jest punktem przegięcia wykresu funkcji
jest punktem przegięcia wykresu funkcji  .
.
Uzyskane wyniki i odpowiedź (uwzględniając również przedziały wypukłości i wklęsłości badanej funkcji) najczęściej zapisujemy w postaci tabeli.

Zauważmy, że funkcja  jest określona dla każdego
jest określona dla każdego  .
.
Obliczamy pierwszą i drugą pochodną funkcji  :
:
i przyrównujemy drugą pochodną do zera:
Stąd wynika, że wykres funkcji  może mieć tylko jeden punkt przegięcia. Dalej badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie a gdzie ujemne:
może mieć tylko jeden punkt przegięcia. Dalej badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie a gdzie ujemne:
oraz
Wyniki umieszczamy w tabeli:

Funkcja jest wypukła na przedziale  , wklęsła na przedziale
, wklęsła na przedziale  , a punkt
, a punkt 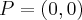 jest punktem przegięcia wykresu funkcji
jest punktem przegięcia wykresu funkcji  .
.