4. Monotoniczność funkcji, ekstrema lokalne i ekstrema globalne
4.4 Zadania
1
Wyznacz ekstrema lokalne i przedziały monotoniczności funkcji określonej wzorem:
- Dziedziną funkcji jest zbiór
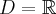 . Funkcja jest rosnąca na każdym z przedziałów:
. Funkcja jest rosnąca na każdym z przedziałów:  ,
, 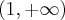 , malejąca na przedziale
, malejąca na przedziale 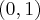 , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne,  , w punkcie
, w punkcie 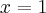 funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 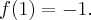
- Dziedziną funkcji jest zbiór
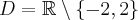 . Funkcja jest rosnąca na każdym z przedziałów:
. Funkcja jest rosnąca na każdym z przedziałów: 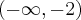 ,
, 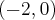 , malejąca na każdym z przedziałów:
, malejąca na każdym z przedziałów: 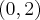 ,
,  , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 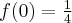 .
. - Dziedziną funkcji jest zbiór
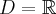 . Funkcja jest malejąca na każdym z przedziałów:
. Funkcja jest malejąca na każdym z przedziałów: 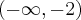 ,
,  , rosnąca na przedziale
, rosnąca na przedziale 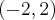 , w punkcie
, w punkcie  funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 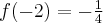 , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 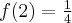 .
. - Dziedziną funkcji jest zbiór
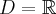 . Funkcja jest rosnąca na każdym z przedziałów:
. Funkcja jest rosnąca na każdym z przedziałów: 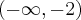 ,
,  , malejąca na przedziale
, malejąca na przedziale 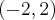 , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 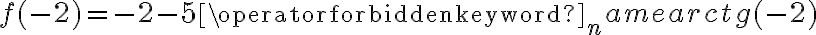 , w punkcie
, w punkcie  funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 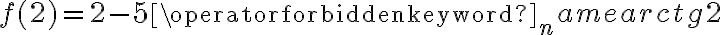 .
.
2
Wyznacz ekstrema lokalne i przedziały monotoniczności funkcji określonej wzorem:
- Dziedziną funkcji jest zbiór
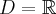 . Funkcja jest rosnąca w całej swojej dziedzinie.
. Funkcja jest rosnąca w całej swojej dziedzinie. - Funkcja jest rosnąca na każdym z przedziałów:
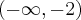 ,
,  , malejąca na przedziale
, malejąca na przedziale 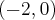 , w punkcie
, w punkcie  funkcja ma minimum lokalne, o wartości
funkcja ma minimum lokalne, o wartości  , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 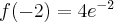 .
. - Dziedziną funkcji jest zbiór
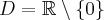 . Funkcja jest rosnąca na każdym z przedziałów:
. Funkcja jest rosnąca na każdym z przedziałów:  ,
, 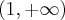 , malejąca na przedziale
, malejąca na przedziale 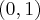 , w punkcie
, w punkcie 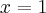 funkcja ma minimum lokalne,
funkcja ma minimum lokalne,  .
. - Dziedziną funkcji jest zbiór
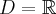 . Funkcja jest rosnąca na każdym z przedziałów:
. Funkcja jest rosnąca na każdym z przedziałów:  ,
, 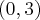 , malejąca na przedziale
, malejąca na przedziale 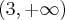 , w punkcie j
, w punkcie j 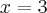 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 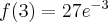 .
.
3
Wyznacz ekstrema lokalne i przedziały monotoniczności funkcji określonej wzorem:
- Dziedziną funkcji jest zbiór
 . Funkcja jest rosnąca na przedziale
. Funkcja jest rosnąca na przedziale 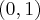 , malejąca na przedziale
, malejąca na przedziale 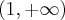 , w punkcie
, w punkcie 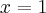 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 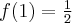 .
. - Dziedziną funkcji jest zbiór
 . Funkcja jest rosnąca na przedziale
. Funkcja jest rosnąca na przedziale 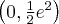 , malejąca na przedziale
, malejąca na przedziale 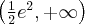 , w punkcie
, w punkcie 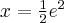 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 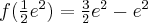 .
. - Dziedziną funkcji jest zbiór
 . Funkcja jest rosnąca na każdym z przedziałów:
. Funkcja jest rosnąca na każdym z przedziałów: 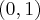 ,
, 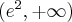 , malejąca na przedziale
, malejąca na przedziale 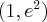 , w punkcie
, w punkcie 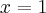 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 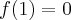 , w punkcie
, w punkcie 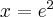 funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 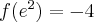 .
.
4
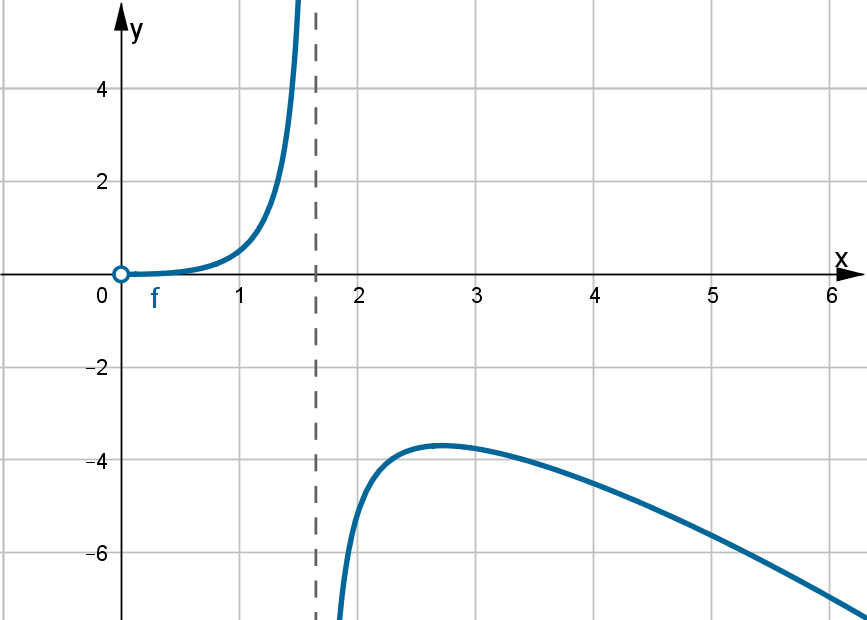
Wyznacz asymptoty, ekstrema lokalne, przedziały monotoniczności oraz naszkicuj wykres funkcji określonej wzorem:
- Dziedziną funkcji jest zbiór
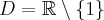 . Funkcja ma asymptotę pionową obustronną
. Funkcja ma asymptotę pionową obustronną 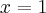 , asymptotę ukośną
, asymptotę ukośną 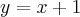 w
w 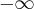 i w
i w 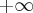 . Funkcja jest malejąca na każdym z przedziałów:
. Funkcja jest malejąca na każdym z przedziałów: 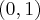 ,
, 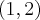 , rosnąca na każdym z przedziałów:
, rosnąca na każdym z przedziałów:  ,
,  , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne,  , w punkcie
, w punkcie  funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 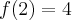 .
.
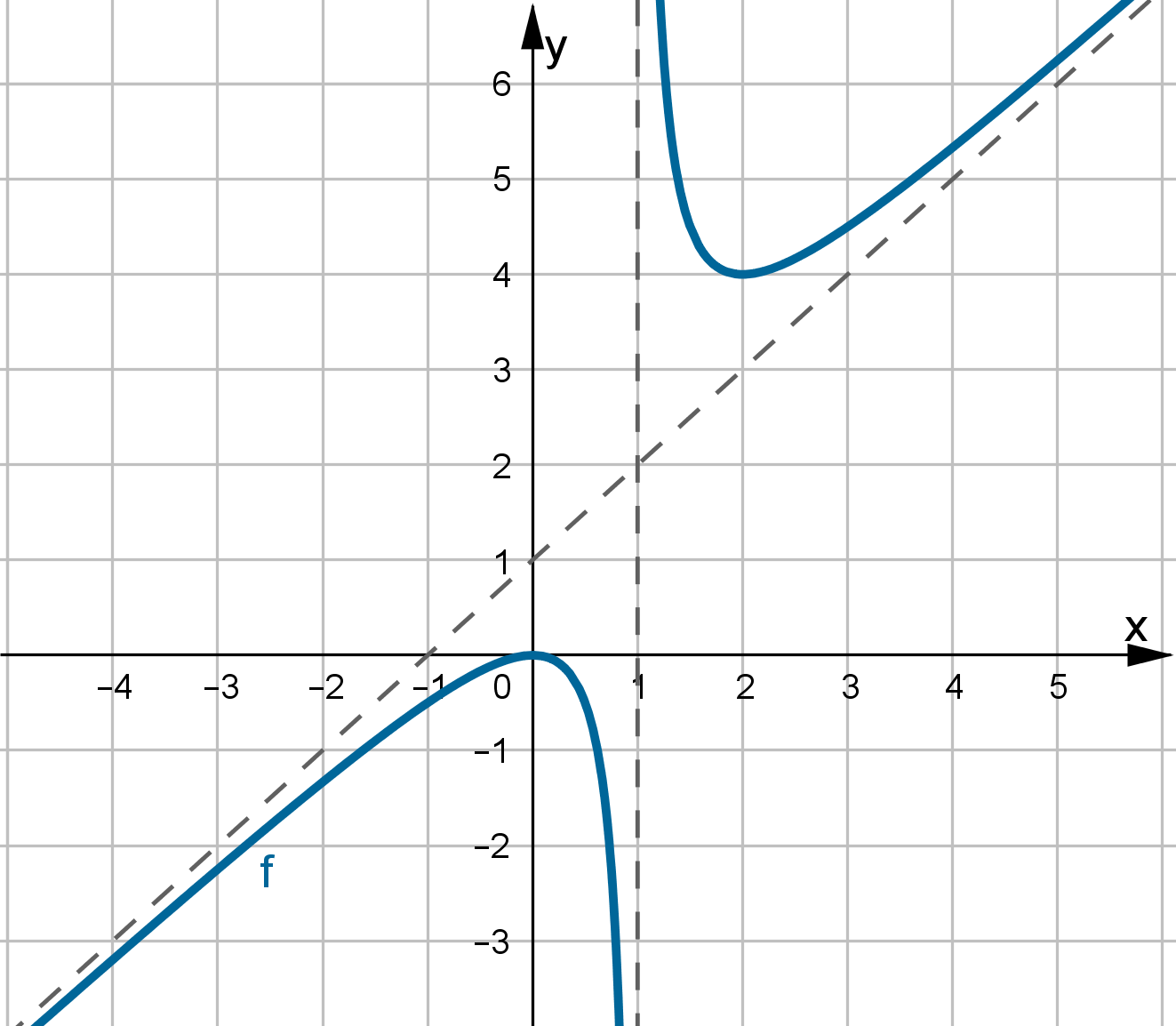
- Dziedziną funkcji jest zbiór
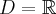 . Funkcja ma asymptotę poziomą
. Funkcja ma asymptotę poziomą 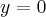 w
w 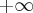 . Funkcja jest rosnąca na przedziale
. Funkcja jest rosnąca na przedziale 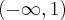 , malejąca na przedziale
, malejąca na przedziale 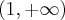 , w punkcie
, w punkcie 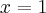 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 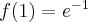 .
.
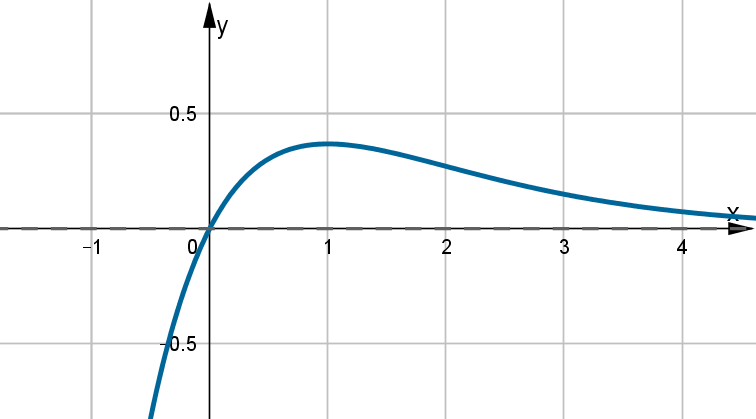
- Dziedziną funkcji jest zbiór
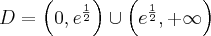 . Funkcja ma asymptotę pionową obustronną
. Funkcja ma asymptotę pionową obustronną 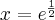 . Funkcja jest rosnąca na każdym z przedziałów
. Funkcja jest rosnąca na każdym z przedziałów 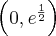 ,
,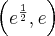 , malejąca na przedziale
, malejąca na przedziale 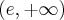 , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 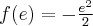 .
.
5
6
7
8
9
10
11

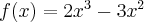
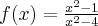
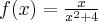
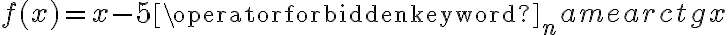
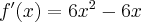
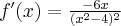
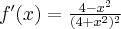
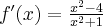
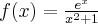
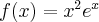
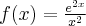
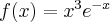
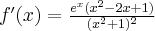
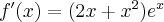
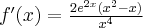
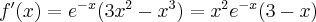

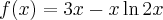
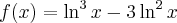

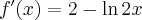
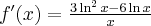
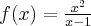
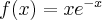
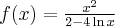

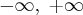
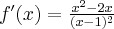
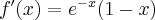
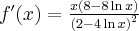
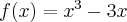
![\left[-\frac32,\frac32\right] \left[-\frac32,\frac32\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/3d37f8f24db07b76ec409152758ed442.png)



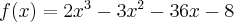
![\left[-3,6\right] \left[-3,6\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/00c68647083b2f383f560b6ad5d18e1c.png)
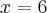
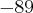
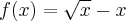
![\left[0,4\right] \left[0,4\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/3a3336efbf8dc022f837ea242eac6177.png)

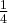
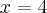

![\left[1,e\right] \left[1,e\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/e39736481a2c1c09c86876a0ced4f203.png)


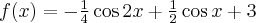
![\left[-\frac\pi2,\pi\right] \left[-\frac\pi2,\pi\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/1486e6af07e678eb58db2c32d27129d2.png)
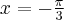
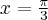
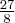

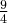
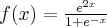
![\left[-1,0\right] \left[-1,0\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/30c62099d861ab81bd5edee7ff9f8135.png)
![\left[-1, 0\right] \left[-1, 0\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/e0ee2ce98c0425348a3c8e433375ea7a.png)

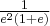
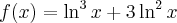
![\left[e^{-3},e^2\right] \left[e^{-3},e^2\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/c58f04d9ed02b443e1d72d25a406c467.png)

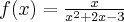
![\left[-2,0\right] \left[-2,0\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/6f7d52e96ec1f58a451ede2a24d276e0.png)
![\left[-2, 0\right] \left[-2, 0\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/344e6b26818e46f5e51bacbcd8fc943f.png)