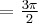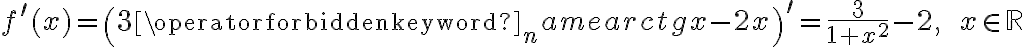6. Badanie przebiegu zmienności funkcji
Przykłady
-
Wyznaczymy asymptoty wykresu funkcji
 . Obliczamy w tym celu granice funkcji na krańcach jej dziedziny:
. Obliczamy w tym celu granice funkcji na krańcach jej dziedziny:Zatem prosta o równaniu
 jest asymptotą poziomą wykresu funkcji w
jest asymptotą poziomą wykresu funkcji w 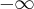 i
i 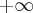 .
.Wykres funkcji nie ma asymptot pionowych.
-
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji
 . Obliczamy w tym celu pochodną funkcji.
. Obliczamy w tym celu pochodną funkcji.Wyznaczamy punkty stacjonarne funkcji:
Badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Zauważmy najpierw, że
 dla każdego
dla każdego  , zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia  . Mamy więc:
. Mamy więc:Zatem funkcja jest malejąca na przedziale
 , rosnąca na przedziale
, rosnąca na przedziale  .
.Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie
 funkcja ma minimum lokalne równe
funkcja ma minimum lokalne równe  .
. -
Wyznaczymy przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji
 . Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie
. Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie  .
.Badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie , a gdzie ujemne. Zauważmy, że
 dla każdego
dla każdego  , zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia  .
.Zatem funkcja jest wypukła na przedziale
 , wklęsła na przedziałach
, wklęsła na przedziałach  ,
,  . Punkty
. Punkty  ,
, 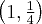 są punktami przegięcia wykresu funkcji.
są punktami przegięcia wykresu funkcji. -
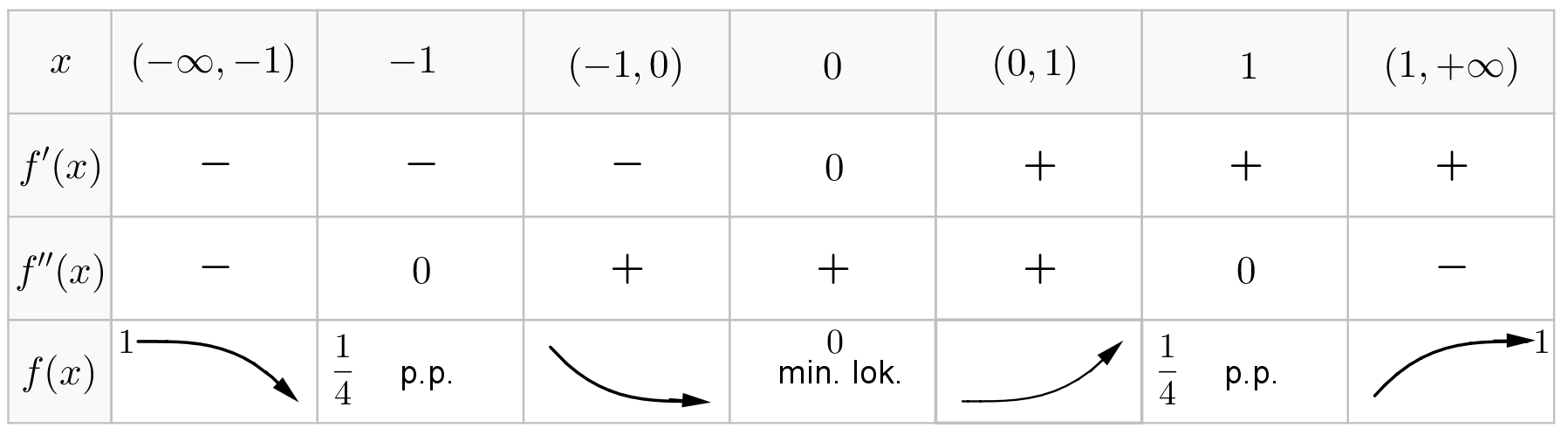
Tabelka przebiegu zmienności funkcji
 .
.
-
Wykres funkcji
 . Zaczynamy od narysowania asymptot, następnie zaznaczamy wyznaczone punkty specjalne (punkty ekstremalne i punkty przegięcia) oraz szkicujemy wykres funkcji na podstawie tabeli.
. Zaczynamy od narysowania asymptot, następnie zaznaczamy wyznaczone punkty specjalne (punkty ekstremalne i punkty przegięcia) oraz szkicujemy wykres funkcji na podstawie tabeli.
- Dziedziną funkcji
 jest zbiór
jest zbiór  .
. - Wyznaczymy asymptoty wykresu funkcji
 . Obliczymy w tym celu granice funkcji na krańcach jej dziedziny:
. Obliczymy w tym celu granice funkcji na krańcach jej dziedziny:
Zatem funkcja ma asymptotę pionową prawostronną
 .
.Zatem prosta o równaniu
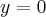 jest asymptotą poziomą wykresu funkcji
jest asymptotą poziomą wykresu funkcji  w
w 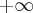 .
. -
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji
 . Obliczamy w tym celu pochodną funkcji.
. Obliczamy w tym celu pochodną funkcji.Wyznaczamy punkty stacjonarne funkcji:
Badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Zauważmy najpierw, że
 dla każdego
dla każdego  , zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia  . Mamy więc:
. Mamy więc:Zatem funkcja jest rosnąca na przedziale
 , malejąca na przedziale
, malejąca na przedziale  .
.Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie
 funkcja ma maksimum lokalne równe
funkcja ma maksimum lokalne równe  .
. -
Wyznaczymy przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji
 . Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie
. Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie  .
.Badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie , a gdzie ujemne. Zauważmy, że
 dla każdego
dla każdego  , zatem znak drugiej pochodnej funkcji będzie taki sam jak znak wyrażenia
, zatem znak drugiej pochodnej funkcji będzie taki sam jak znak wyrażenia  .
.Zatem funkcja
 jest wklęsła na przedziale
jest wklęsła na przedziale  , wypukła na przedziale
, wypukła na przedziale 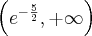 , punkt
, punkt 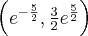 jest punktem przegięcia wykresu funkcji.
jest punktem przegięcia wykresu funkcji. -
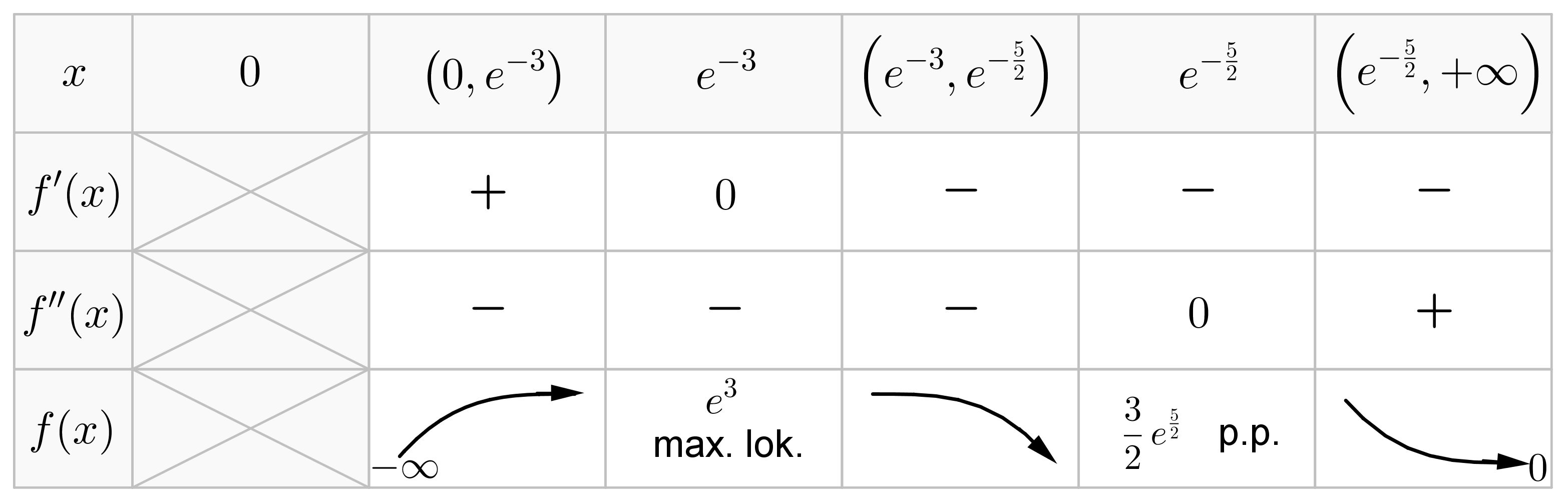
Tabelka przebiegu zmienności funkcji
 .
.
-
Wykres funkcji
 . Zaczynamy od narysowania asymptot, następnie zaznaczamy wyznaczone punkty specjalne (punkty ekstremalne i punkty przegięcia) oraz szkicujemy wykres funkcji na podstawie tabeli.
. Zaczynamy od narysowania asymptot, następnie zaznaczamy wyznaczone punkty specjalne (punkty ekstremalne i punkty przegięcia) oraz szkicujemy wykres funkcji na podstawie tabeli.
- Dziedziną funkcji
 jest zbiór
jest zbiór  .
. -
Wyznaczymy asymptoty wykresu funkcji
 . Obliczymy w tym celu granice funkcji na krańcach jej dziedziny:
. Obliczymy w tym celu granice funkcji na krańcach jej dziedziny:Ponieważ obie policzone powyżej granice są niewłaściwe więc wykres funkcji nie ma symptoty poziomej. Sprawdzamy istnienie asymptot ukośnych wykresu funkcji w
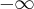 i
i 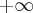 .
.Prosta o równaniu
 , czyli
, czyli  jest asymptotą ukośną wykresu funkcji w
jest asymptotą ukośną wykresu funkcji w 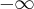 .
.Zatem prosta o równaniu
 jest asymptotą ukośną wykresu funkcji w
jest asymptotą ukośną wykresu funkcji w 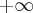 .
.Podsumowując otrzymujemy, że prosta o równaniu
 jest asymptotą ukośną wykresu funkcji w
jest asymptotą ukośną wykresu funkcji w 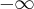 , prosta prosta o równaniu
, prosta prosta o równaniu  jest asymptotą ukośną wykresu funkcji w
jest asymptotą ukośną wykresu funkcji w 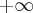 . Wykres funkcji
. Wykres funkcji  nie ma asymptot pionowych.
nie ma asymptot pionowych. -
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji
 . Obliczamy w tym celu pochodną funkcji.
. Obliczamy w tym celu pochodną funkcji.Wyznaczamy punkty stacjonarne funkcji:
Badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Zauważmy najpierw, że
 dla każdego
dla każdego  , zatem znak pochodnej funkcji będzie taki sam jak znak wyrażenia
, zatem znak pochodnej funkcji będzie taki sam jak znak wyrażenia  . Mamy więc:
. Mamy więc:Zatem funkcja jest malejąca na każdym z przedziałów
 ,
, 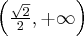 , rosnąca na przedziale
, rosnąca na przedziale  . Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie
. Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie 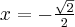 funkcja ma minimum lokalne równe
funkcja ma minimum lokalne równe  , zaś w punkcie
, zaś w punkcie  funkcja ma maksimum lokalne równe
funkcja ma maksimum lokalne równe 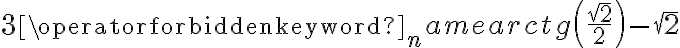 .
. -
Wyznaczymy przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji
 . Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie
. Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie  .
.Badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Zauważmy, że
 dla każdego
dla każdego  , zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia  .
.Zatem funkcja
 jest wypukła na przedziale
jest wypukła na przedziale  , wklęsła na przedziale
, wklęsła na przedziale  , punkt
, punkt  jest punktem przegięcia wykresu funkcji.
jest punktem przegięcia wykresu funkcji. -
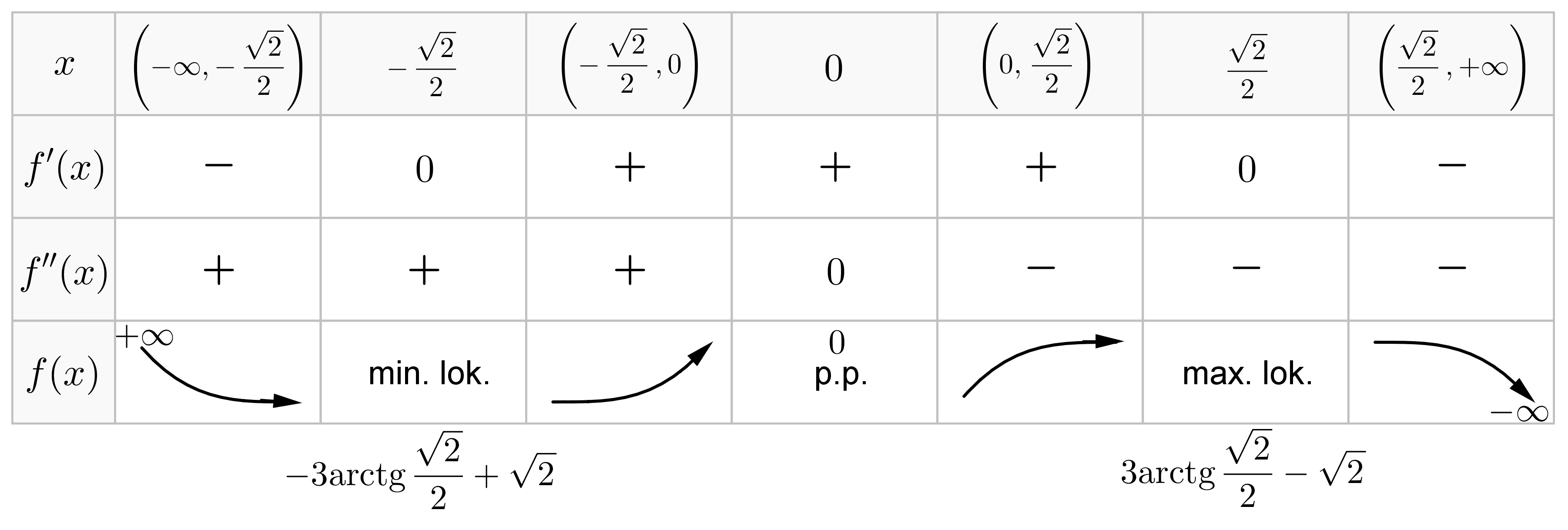
Tabelka przebiegu zmienności funkcji
 .
.
-
Wykres funkcji
 . Zaczynamy od narysowania asymptot, następnie zaznaczamy wyznaczone punkty specjalne (punkty ekstremalne i punkty przegięcia) oraz szkicujemy wykres funkcji na podstawie tabeli.
. Zaczynamy od narysowania asymptot, następnie zaznaczamy wyznaczone punkty specjalne (punkty ekstremalne i punkty przegięcia) oraz szkicujemy wykres funkcji na podstawie tabeli.


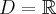

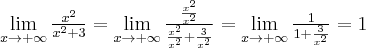




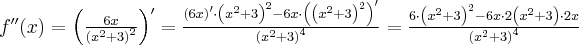







![\lim\limits_{x\to 0^+} \frac{4+\ln x}{x}=\lim\limits_{x\to 0^+} (4+\ln x)\cdot \frac{1}{x}=\left[(4+\ln 0^+)\cdot \frac{1}{0^+}=-\infty\cdot (+\infty)\right]=-\infty \lim\limits_{x\to 0^+} \frac{4+\ln x}{x}=\lim\limits_{x\to 0^+} (4+\ln x)\cdot \frac{1}{x}=\left[(4+\ln 0^+)\cdot \frac{1}{0^+}=-\infty\cdot (+\infty)\right]=-\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/0e15e5c8539e7d53566dd9503d9352ab.png)
![\lim\limits_{x\to+ \infty} \frac{4+\ln x}{x}=\left[\frac{+\infty}{+\infty}\right]\stackrel{[H]}{=}\lim\limits_{x\to +\infty}\frac{\frac1x}{1}=\lim\limits_{x\to +\infty}\frac{1}{x}=\left[\frac{1}{+\infty}\right]=0 \lim\limits_{x\to+ \infty} \frac{4+\ln x}{x}=\left[\frac{+\infty}{+\infty}\right]\stackrel{[H]}{=}\lim\limits_{x\to +\infty}\frac{\frac1x}{1}=\lim\limits_{x\to +\infty}\frac{1}{x}=\left[\frac{1}{+\infty}\right]=0](https://port.edu.p.lodz.pl/filter/tex/pix.php/d9448ffb6c1a09ff78f17d7908456b2a.png)
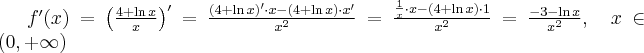
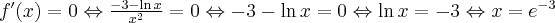

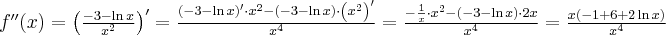





![\lim\limits_{x\to -\infty} f(x)=\lim\limits_{x\to -\infty}\left(3\operatorname{arctg}x-2x\right)=\left[{3\operatorname{arctg}(-\infty)-2\cdot(-\infty)=\frac {-3\pi}{2}}+\infty\right]=+\infty \lim\limits_{x\to -\infty} f(x)=\lim\limits_{x\to -\infty}\left(3\operatorname{arctg}x-2x\right)=\left[{3\operatorname{arctg}(-\infty)-2\cdot(-\infty)=\frac {-3\pi}{2}}+\infty\right]=+\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/30ea6d168837bd5b21d43d217e5e5f44.png)
![\lim\limits_{x\to+ \infty} f(x)=\lim\limits_{x\to+ \infty}\left(3\operatorname{arctg}x-2x\right)=\left[{3\operatorname{arctg}(+\infty)-2\cdot\infty=\frac {3\pi}{2}}-\infty\right]=-\infty \lim\limits_{x\to+ \infty} f(x)=\lim\limits_{x\to+ \infty}\left(3\operatorname{arctg}x-2x\right)=\left[{3\operatorname{arctg}(+\infty)-2\cdot\infty=\frac {3\pi}{2}}-\infty\right]=-\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/467362e47bd4f2af6f66355d15955973.png)

![=\left[\frac{3\operatorname{arctg}(-\infty)}{-\infty}-2 =\frac{-\frac {3\pi}{2}}{-\infty}-2\right] =\left[\frac{3\operatorname{arctg}(-\infty)}{-\infty}-2 =\frac{-\frac {3\pi}{2}}{-\infty}-2\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/62c379a9f7a1cb0b2ce70618ab4d2447.png)



![=\left[3\operatorname{arctg}(-\infty)\right] =\left[3\operatorname{arctg}(-\infty)\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/e03ec2c19fc0a4b8314d1b40ecc1591e.png)



![=\left[\frac{3\operatorname{arctg}(+\infty)}{+\infty}-2=\frac{\frac {3\pi}{2}}{+\infty}-2\right] =\left[\frac{3\operatorname{arctg}(+\infty)}{+\infty}-2=\frac{\frac {3\pi}{2}}{+\infty}-2\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/862e15519d3bf493f62f47ef1bdfe697.png)

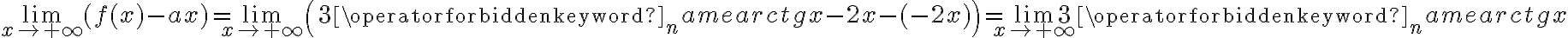
![=\left[3\operatorname{arctg}(+\infty)\right] =\left[3\operatorname{arctg}(+\infty)\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/57cd78e0649f9719d2850057c76120f9.png)