4.3 Ekstrema globalne funkcji
Przykłady
Wyznaczymy najmniejszą i największą wartość (ekstrema globalne) funkcji 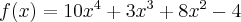 na przedziale
na przedziale ![\left[-1,2\right] \left[-1,2\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/36e0c00681a7b9d8a5526b7f5f8868ec.png) .
.
Wyznaczymy najpierw punkty wewnątrz przedziału, w których funkcja może mieć ekstrema lokalne.
Funkcja  jest różniczkowalna w każdym punkcie przedziału
jest różniczkowalna w każdym punkcie przedziału  , zatem punkt
, zatem punkt  jest jedynym punktem w tym przedziale, w którym funkcja może mieć ekstremum lokalne.
jest jedynym punktem w tym przedziale, w którym funkcja może mieć ekstremum lokalne.
Obliczymy teraz wartości funkcji w punktach, w których  może osiągnąć ekstrema globalne, czyli punkcie
może osiągnąć ekstrema globalne, czyli punkcie  oraz w punktach będących krańcami podanego przedziału:
oraz w punktach będących krańcami podanego przedziału:
Zatem w przedziale ![\left[-1,2\right] \left[-1,2\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/36e0c00681a7b9d8a5526b7f5f8868ec.png) największą wartość (maksimum globalne) dana funkcja przyjmuje dla
największą wartość (maksimum globalne) dana funkcja przyjmuje dla  i wartość ta jest równa
i wartość ta jest równa 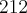 , najmniejszą wartość (minimum globalne) przyjmuje dla
, najmniejszą wartość (minimum globalne) przyjmuje dla  i wartość jest równa
i wartość jest równa  .
.
Możemy też zapisać:
Wyznaczymy najmniejszą i największą wartość (ekstrema globalne) funkcji  na przedziale
na przedziale ![\left[-\sqrt3,\sqrt3\right] \left[-\sqrt3,\sqrt3\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/b1297a8d5a2ce17fc2e847c64b504bf9.png) .
.
Wyznaczymy najmniejszą i największą wartość (ekstrema globalne) funkcji 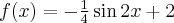 na przedziale
na przedziale ![\left[-\frac\pi2,\frac{3\pi}4\right] \left[-\frac\pi2,\frac{3\pi}4\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/a6499fbe992129b76ad723a4a416c17c.png) .
.
Wyznaczymy najpierw punkty wewnątrz przedziału, w których funkcja może mieć ekstrema lokalne.
Funkcja  jest różniczkowalna w każdym punkcie przedziału
jest różniczkowalna w każdym punkcie przedziału 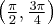 , zatem jedynymi punktami należącymi do tego przedziału, w których funkcja może mieć ekstrema lokalne są:
, zatem jedynymi punktami należącymi do tego przedziału, w których funkcja może mieć ekstrema lokalne są:  ,
,  .
.
Obliczymy teraz wartości funkcji w wyznaczonych wyżej punktach oraz w punktach, które są krańcami podanego przedziału.
Zatem w przedziale ![\left[-\frac\pi2,\frac{3\pi}4\right] \left[-\frac\pi2,\frac{3\pi}4\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/a6499fbe992129b76ad723a4a416c17c.png) największą wartość (maksimum globalne) dana funkcja przyjmuje dla
największą wartość (maksimum globalne) dana funkcja przyjmuje dla  ,
, 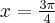 i wartość ta jest równa
i wartość ta jest równa 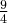 , najmniejszą wartość (minimum globalne) przyjmuje dla
, najmniejszą wartość (minimum globalne) przyjmuje dla  i wartość ta jest równa
i wartość ta jest równa  .
.
Wyznaczymy najmniejszą i największą wartość (ekstrema globalne) funkcji  na przedziale
na przedziale ![\left[-2,1\right] \left[-2,1\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/433b65bbd2fe21fcc67ec374215ff1c8.png) .
.
Wyznaczymy najpierw punkty wewnątrz przedziału, w których funkcja może mieć ekstrema lokalne.
Funkcja  jest różniczkowalna w każdym punkcie przedziału
jest różniczkowalna w każdym punkcie przedziału  , zatem punkty
, zatem punkty  ,
,  są jedynymi w tym przedziale, w których funkcja może mieć ekstrema lokalne.
są jedynymi w tym przedziale, w których funkcja może mieć ekstrema lokalne.
Obliczymy teraz wartości funkcji w wyznaczonych wyżej punktach oraz w punktach, które są krańcami podanego przedziału.
Zatem w przedziale ![\left[-2,1\right] \left[-2,1\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/433b65bbd2fe21fcc67ec374215ff1c8.png) największą wartość (maksimum globalne) dana funkcja przyjmuje dla
największą wartość (maksimum globalne) dana funkcja przyjmuje dla 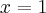 i wartość ta jest równa
i wartość ta jest równa  , najmniejszą wartość (minimum globalne) przyjmuje dla
, najmniejszą wartość (minimum globalne) przyjmuje dla  i wartość ta jest równa
i wartość ta jest równa  .
.
Wyznaczymy najmniejszą i największą wartość (ekstrema globalne) funkcji  na przedziale
na przedziale ![\left[e^{-2},e^2\right] \left[e^{-2},e^2\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/edeca57f6f48fa40bf719bc7bd30b885.png) .
.
Wyznaczymy najpierw punkty wewnątrz przedziału, w których funkcja może mieć ekstrema lokalne.
Funkcja  jest różniczkowalna w każdym punkcie przedziału
jest różniczkowalna w każdym punkcie przedziału  , zatem punkty
, zatem punkty  ,
,  są jedynymi w tym przedziale, w których funkcja może mieć ekstrema lokalne.
są jedynymi w tym przedziale, w których funkcja może mieć ekstrema lokalne.
Obliczymy teraz wartości funkcji w wyznaczonych wyżej punktach oraz w punktach, które są krańcami podanego przedziału.
Zatem w przedziale ![\left[e^{-2},e^2\right] \left[e^{-2},e^2\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/edeca57f6f48fa40bf719bc7bd30b885.png) największą wartość (maksimum globalne) dana funkcja przyjmuje dla
największą wartość (maksimum globalne) dana funkcja przyjmuje dla  i wartość ta jest równa
i wartość ta jest równa  , najmniejszą wartość (minimum globalne) przyjmuje w punkcie
, najmniejszą wartość (minimum globalne) przyjmuje w punkcie  i wartość ta jest równa
i wartość ta jest równa  .
.
Wyznaczymy najmniejszą i największą wartość (ekstrema globalne) funkcji ![f(x)=6x-9\sqrt[3]{x^2} f(x)=6x-9\sqrt[3]{x^2}](https://port.edu.p.lodz.pl/filter/tex/pix.php/eb62f0d910c81568987a04befe5e023a.png) na przedziale
na przedziale ![\left[-1,\sqrt{8}\right] \left[-1,\sqrt{8}\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/373666af5a368bfec033967341dff2ac.png) .
.
Wyznaczymy najpierw punkty wewnątrz przedziału, w których funkcja może mieć ekstrema lokalne.
Ponadto funkcja  nie jest różniczkowalna w
nie jest różniczkowalna w  (można pokazać, że
(można pokazać, że  oraz
oraz  ). To oznacza, że
). To oznacza, że  może mieć ekstrema lokalne jedynie w punktach
może mieć ekstrema lokalne jedynie w punktach  i
i 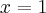 .
.
Obliczymy teraz wartości funkcji w wyznaczonych wyżej punktach oraz w punktach, które są krańcami podanego przedziału.
Zatem w przedziale ![\left[-1,\sqrt{8}\right] \left[-1,\sqrt{8}\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/373666af5a368bfec033967341dff2ac.png) największą wartość (maksimum globalne) dana funkcja przyjmuje dla
największą wartość (maksimum globalne) dana funkcja przyjmuje dla  i wartość ta jest równa
i wartość ta jest równa  , najmniejszą wartość (minimum globalne) przyjmuje dla
, najmniejszą wartość (minimum globalne) przyjmuje dla  i wartość ta jest równa
i wartość ta jest równa  .
.





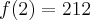
![\displaystyle \max _{x\in \left[-1,2\right]} f(x)=212=f(2) \displaystyle \max _{x\in \left[-1,2\right]} f(x)=212=f(2)](https://port.edu.p.lodz.pl/filter/tex/pix.php/8234effd116b04e91a7f87805d8f4962.png)
![\quad \displaystyle \min _{x\in \left[-1,2\right]} f(x)=-4=f(0) \quad \displaystyle \min _{x\in \left[-1,2\right]} f(x)=-4=f(0)](https://port.edu.p.lodz.pl/filter/tex/pix.php/d2d68bb9e08434d01982aba7b6dd7c6e.png)









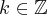




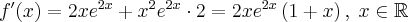






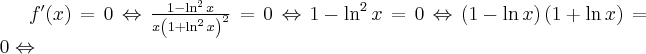





![f^\prime(x)=6-9\cdot \frac{2}{3} x^{-\frac{1}{3}}=6-\frac{6}{\sqrt[3]{x}}, \; x\in \mathbb R\setminus \{0\} f^\prime(x)=6-9\cdot \frac{2}{3} x^{-\frac{1}{3}}=6-\frac{6}{\sqrt[3]{x}}, \; x\in \mathbb R\setminus \{0\}](https://port.edu.p.lodz.pl/filter/tex/pix.php/cb566b4956551492c2b59f07af7ac320.png)
![f^\prime(x)=0 \Leftrightarrow 6-\frac{6}{\sqrt[3]{x}}=0\Leftrightarrow \sqrt[3]{x}=1 \Leftrightarrow x=1 f^\prime(x)=0 \Leftrightarrow 6-\frac{6}{\sqrt[3]{x}}=0\Leftrightarrow \sqrt[3]{x}=1 \Leftrightarrow x=1](https://port.edu.p.lodz.pl/filter/tex/pix.php/3bd36848ca99f6f7ce890b29ed577e59.png)


