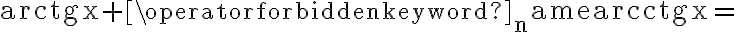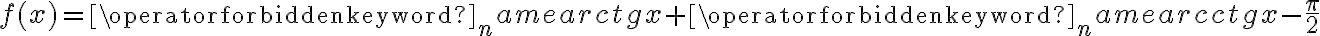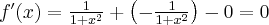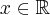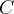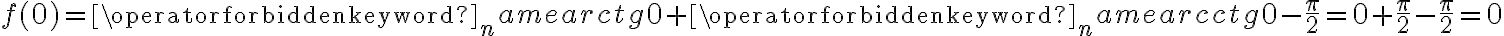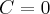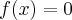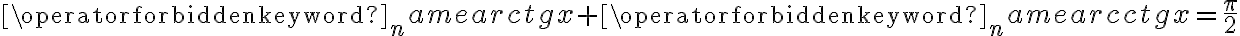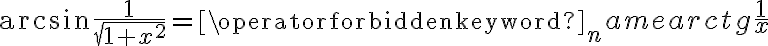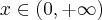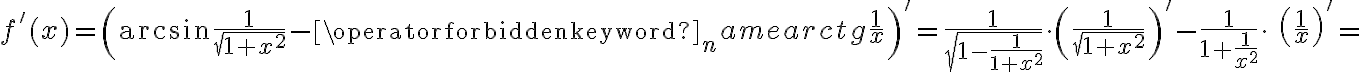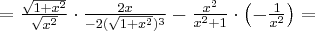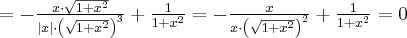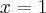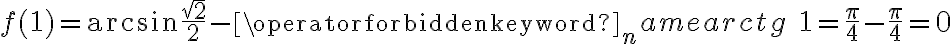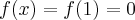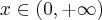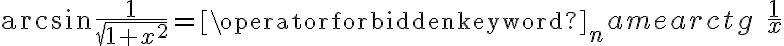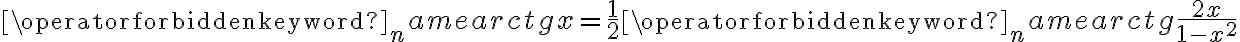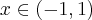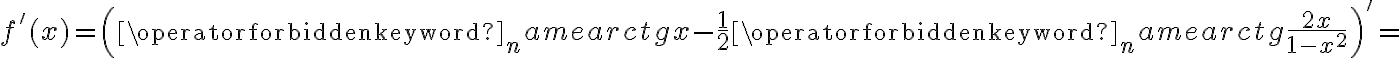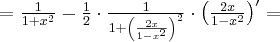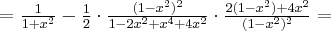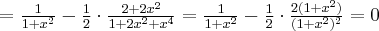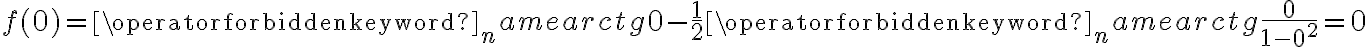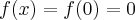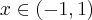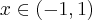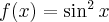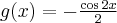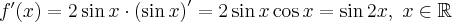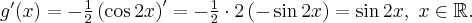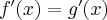2.1 Twierdzenie Rolle'a i twierdzenie Lagrange'a
Przykłady
1
2
3
Rozważmy funkcję 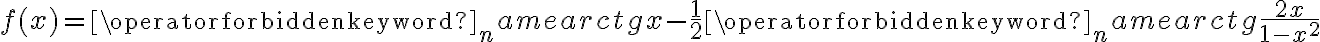 . Zauważmy, że jej dziedziną jest zbiór
. Zauważmy, że jej dziedziną jest zbiór 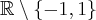 , zatem funkcja
, zatem funkcja  jest poprawnie określona na przedziale
jest poprawnie określona na przedziale 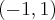 . Obliczmy pochodną funkcji
. Obliczmy pochodną funkcji  :
:
Obliczamy pierwszą i drugą pochodną funkcji  :
:
Zatem 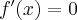 na każdym przedziale zawartym w dziedzinie tej funkcji, zatem w szczególności na
na każdym przedziale zawartym w dziedzinie tej funkcji, zatem w szczególności na 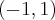 . Na mocy wniosku 1 otrzymujemy, że
. Na mocy wniosku 1 otrzymujemy, że  jest stała na tym przedziale, czyli istnieje stała
jest stała na tym przedziale, czyli istnieje stała  taka, że dla każdego
taka, że dla każdego 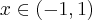 zachodzi równość
zachodzi równość 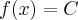 .
.
Obliczymy wartość funkcji  dla argumentu
dla argumentu  .
.