Rachunek różniczkowy funkcji jednej zmiennej

Ćwiczenie 0

Dokończ poprawnie zdanie wybierając jedną z odpowiedzi.

Zobacz podpowiedź:

Ćwiczenie 1

Zastanów się, które rysunki przedstawiają wykresy funkcji wypukłej/wklęsłej na poszczególnych przedziałach dziedziny.

Ćwiczenie 2

Dokończ zdanie wybierając poprawne odpowiedzi.

Podpowiedź

Ćwiczenie 3

Uzupełnij luki.

Ćwiczenie 4

Druga pochodna funkcji 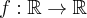$f :\mathbb{R}\to\mathbb{R}$ dana jest wzorem $f''(x)=x+3$.

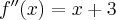Ćwiczenie 4a

Dany jest wykres drugiej pochodnej funkcji 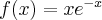$f(x)=xe^{-x}$. Dopasuj własności: wypukła/wklęsła do poszczególnych fragmentów wykresu.

Ćwiczenie 4b

Druga pochodna funkcji 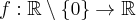$f:\mathbb{R}\setminus\{0\}\to\mathbb{R}$ jest dodatnia dla 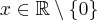$x\in\mathbb{R}\setminus\{0\}$. Zastanów się, czy funkcja może mieć wykres przedstawiony poniżej.

Ćwiczenie 4c

Połącz w pary: wzór i własność funkcji.

Przyciągnij wzory do własności.

Ćwiczenie 4d

Połącz w pary: wykres i własność funkcji.

Ćwiczenie 4e

Druga pochodna funkcji $f$ jest ujemna w całej dziedzinie. Zastanów się, czy funkcja może mieć wykres przedstawiony poniżej.

Ćwiczenie 5

Wiedząc, że funkcja $f$ jest różniczkowalna w punkcie $5$, uzupełnij trzeci wiersz tabeli.

Zawartość pustych pól w tabeli możesz zmienić poprzez kliknięcie.

Ćwiczenie 6

Wybrane informacje o drugiej pochodnej pewnej funkcji 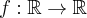$f:\mathbb{R}\rightarrow \mathbb{R}$ zawarte są w poniższej tabeli.

Wybierz rysunki mogące przedstawiać wykres funkcji $f$.

Przenieś wybrane rysunki do obszaru znajdującego się nad nimi.

Ćwiczenie 7

Wybrane informacje o drugiej pochodnej pewnej dwukrotnie różniczkowalnej funkcji 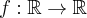$f:\mathbb{R}\rightarrow \mathbb{R}$ zawarte są w poniższej tabeli. Uzupełnij trzeci wiersz tabeli.

Zawartość pustych pól w tabeli możesz zmienić poprzez kliknięcie.