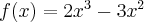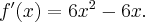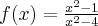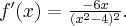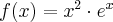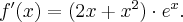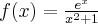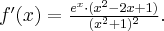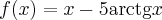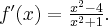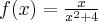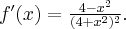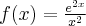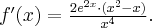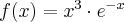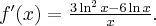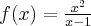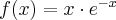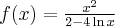3. Monotoniczność funkcji, ekstrema lokalne i ekstrema globalne
3.4 Zadania
Zadanie 1
Wyznacz ekstrema lokalne i przedziały monotoniczności funkcji określonej wzorem:
Odpowiedź: Dziedziną funkcji jest zbiór 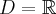 . Funkcja jest rosnąca w każdym z przedziałów:
. Funkcja jest rosnąca w każdym z przedziałów:  ,
, 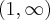 , malejąca w przedziale
, malejąca w przedziale 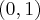 , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne,  , w punkcie
, w punkcie 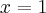 funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 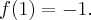
Odpowiedź: Dziedziną funkcji jest zbiór 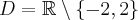 . Funkcja jest rosnąca w każdym z przedziałów:
. Funkcja jest rosnąca w każdym z przedziałów: 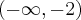 ,
, 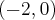 , malejąca w każdym z przedziałów:
, malejąca w każdym z przedziałów: 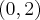 ,
, 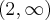 w punkcie
w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 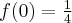 .
.
Funkcja jest rosnąca w każdym z przedziałów: 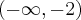 ,
, 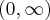 ,
,
malejąca w przedziale 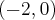 , w punkcie
, w punkcie  funkcja ma minimum lokalne, o wartości
funkcja ma minimum lokalne, o wartości  , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 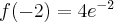 .
.
Odpowiedź: Dziedziną funkcji jest zbiór 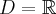 . Funkcja jest rosnąca w całej swojej dziedzinie.
. Funkcja jest rosnąca w całej swojej dziedzinie.
Odpowiedź: Dziedziną funkcji jest zbiór 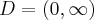 . Funkcja jest rosnąca w przedziale
. Funkcja jest rosnąca w przedziale 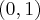 , malejąca w przedziale
, malejąca w przedziale 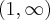 , w punkcie
, w punkcie 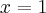 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 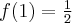 .
.
Odpowiedź: Dziedziną funkcji jest zbiór 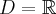 . Funkcja jest rosnąca w każdym z przedziałów:
. Funkcja jest rosnąca w każdym z przedziałów: 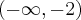 ,
, 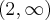 , malejąca w przedziale
, malejąca w przedziale 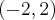 , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 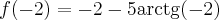 , w punkcie
, w punkcie  funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 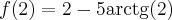 .
.
Odpowiedź: Dziedziną funkcji jest zbiór 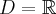 . Funkcja jest malejąca w każdym z przedziałów:
. Funkcja jest malejąca w każdym z przedziałów: 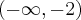 ,
,
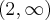 , rosnąca w przedziale
, rosnąca w przedziale 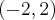 , w punkcie
, w punkcie  funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 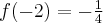 , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 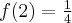 .
.
Odpowiedź: Dziedziną funkcji jest zbiór 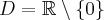 . Funkcja jest rosnąca w każdym z przedziałów:
. Funkcja jest rosnąca w każdym z przedziałów:  ,
, 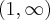 , malejąca w przedziale
, malejąca w przedziale 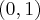 , w punkcie
, w punkcie 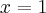 funkcja ma minimum lokalne,
funkcja ma minimum lokalne,  .
.
Odpowiedź: Dziedziną funkcji jest zbiór 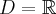 . Funkcja jest rosnąca w każdym z przedziałów:
. Funkcja jest rosnąca w każdym z przedziałów:  ,
, 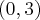 , malejąca w przedziale
, malejąca w przedziale 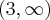 , w punkcie j
, w punkcie j 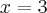 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 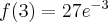 .
.
Odpowiedź: Dziedziną funkcji jest zbiór 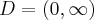 . Funkcja jest rosnąca w przedziale
. Funkcja jest rosnąca w przedziale 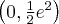 , malejąca w przedziale
, malejąca w przedziale 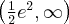 , w punkcie
, w punkcie 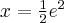 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 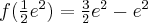 .
.
Odpowiedź: Dziedziną funkcji jest zbiór 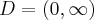 . Funkcja jest rosnąca w każdym z przedziałów:
. Funkcja jest rosnąca w każdym z przedziałów: 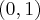 ,
, 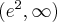 , malejąca w przedziale
, malejąca w przedziale 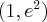 , w punkcie
, w punkcie 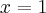 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 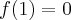 , w punkcie
, w punkcie 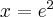 funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 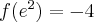 .
.
Zadanie 2
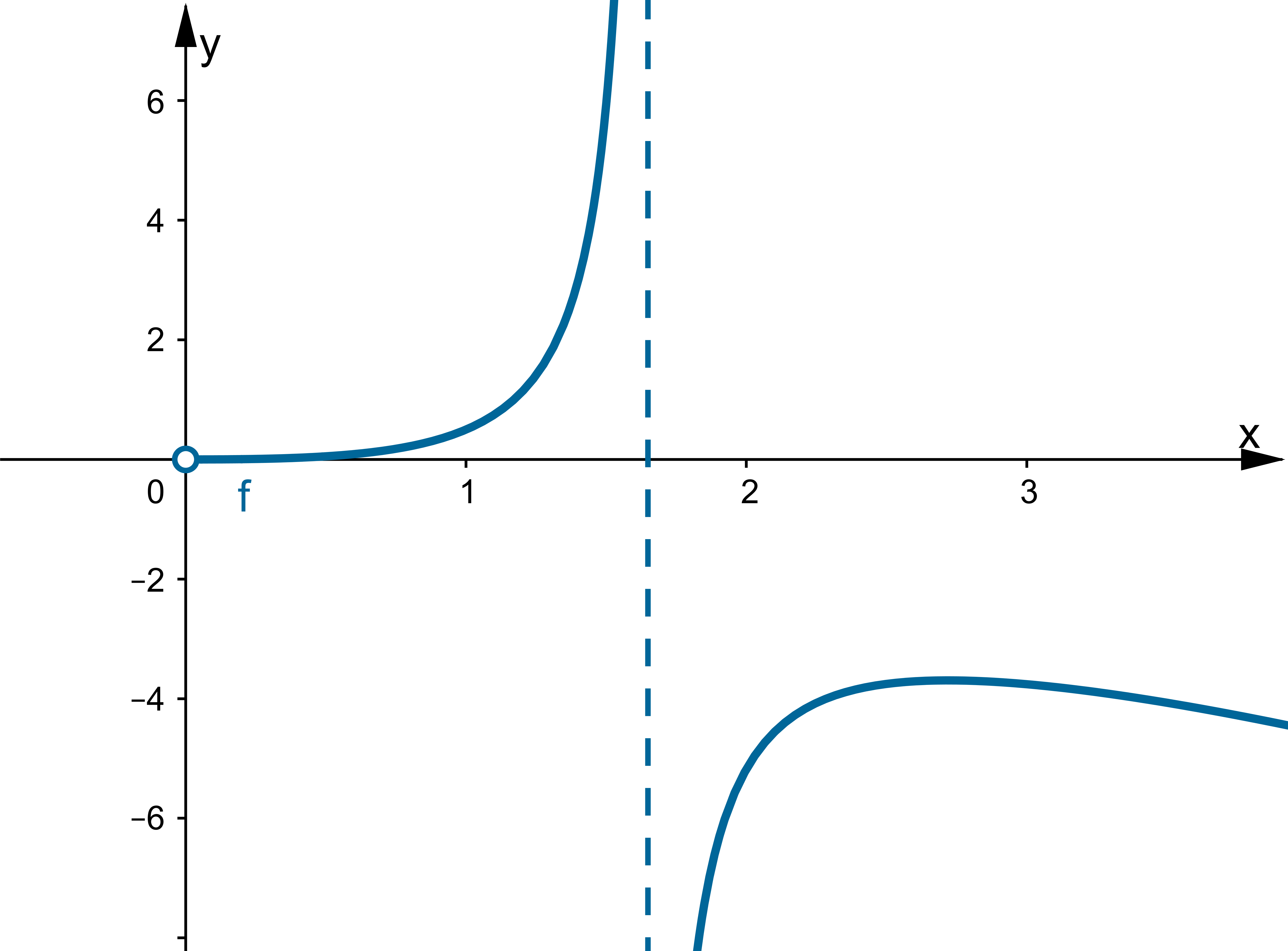
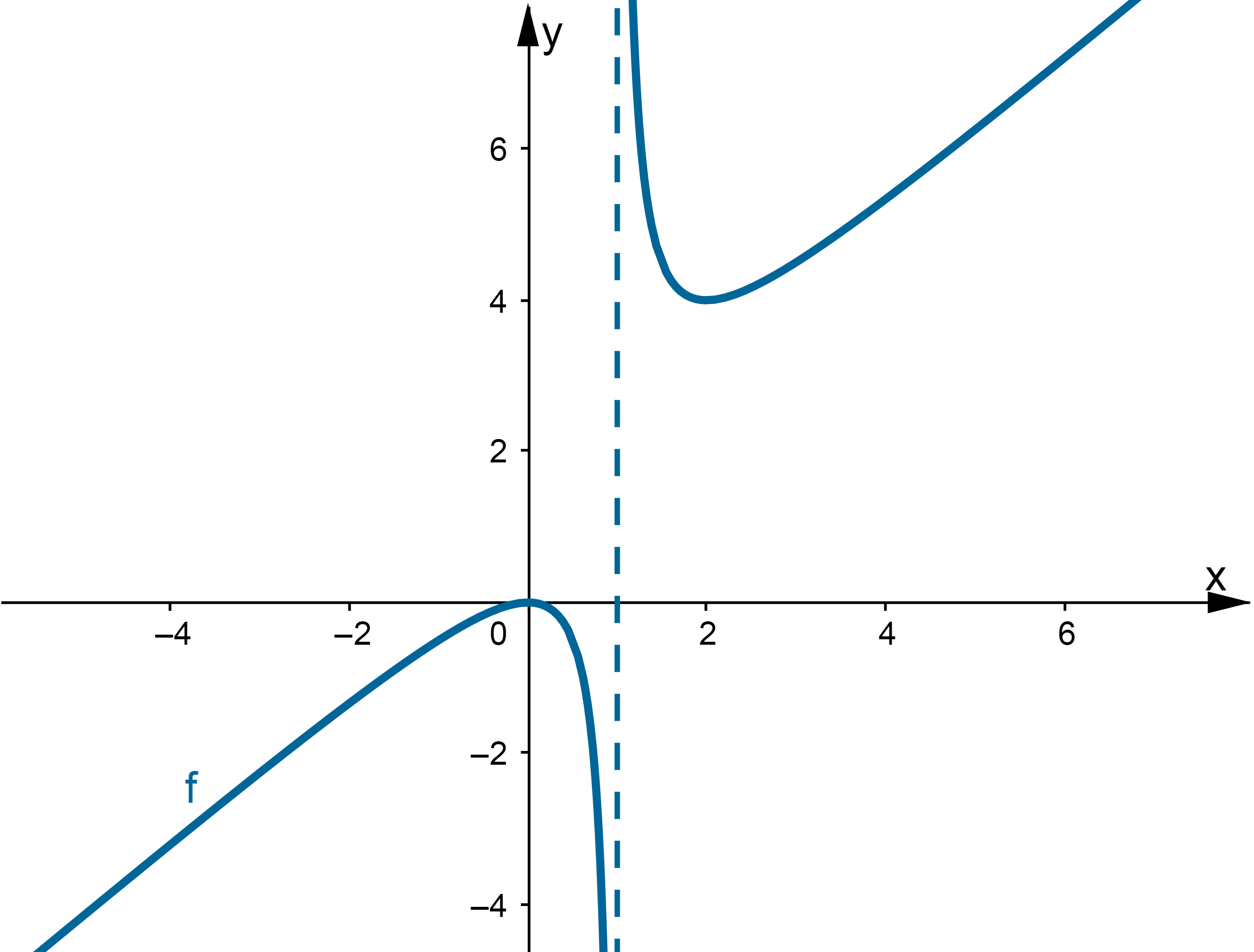
Wyznacz asymptoty, ekstrema lokalne, przedziały monotoniczności oraz naszkicuj wykres funkcji określonej wzorem:
Wskazówka: Asymptotę pionową wykres funkcji  może posiadać w punkcie
może posiadać w punkcie 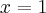 , ukośną w
, ukośną w 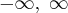 ,
, 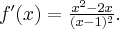
Odpowiedź: Dziedziną funkcji jest zbiór 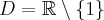 . Funkcja ma asymptotę pionową obustronną
. Funkcja ma asymptotę pionową obustronną 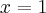 , asymptotę ukośną
, asymptotę ukośną 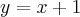 w
w 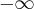 i w
i w 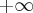 . Funkcja jest malejąca w każdym z przedziałów:
. Funkcja jest malejąca w każdym z przedziałów: 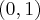 ,
, 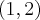 , rosnąca w każdym z przedziałów:
, rosnąca w każdym z przedziałów:  ,
, 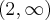 , w punkcie
, w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne,  , w punkcie
, w punkcie  funkcja ma minimum lokalne,
funkcja ma minimum lokalne, 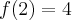 .
.
Wskazówka: Asymptotę ukośną wykres funkcji  może posiadać w
może posiadać w 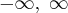 , asymptoty pionowej wykres funkcji
, asymptoty pionowej wykres funkcji  nie posiada.
nie posiada.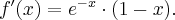
Odpowiedź: Dziedziną funkcji jest zbiór 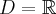 . Funkcja ma asymptotę poziomą
. Funkcja ma asymptotę poziomą 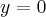 w
w 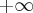 . Funkcja jest rosnąca w przedziale
. Funkcja jest rosnąca w przedziale 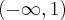 , malejąca w przedziale
, malejąca w przedziale 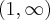 , w punkcie
, w punkcie 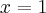 funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 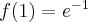 .
.
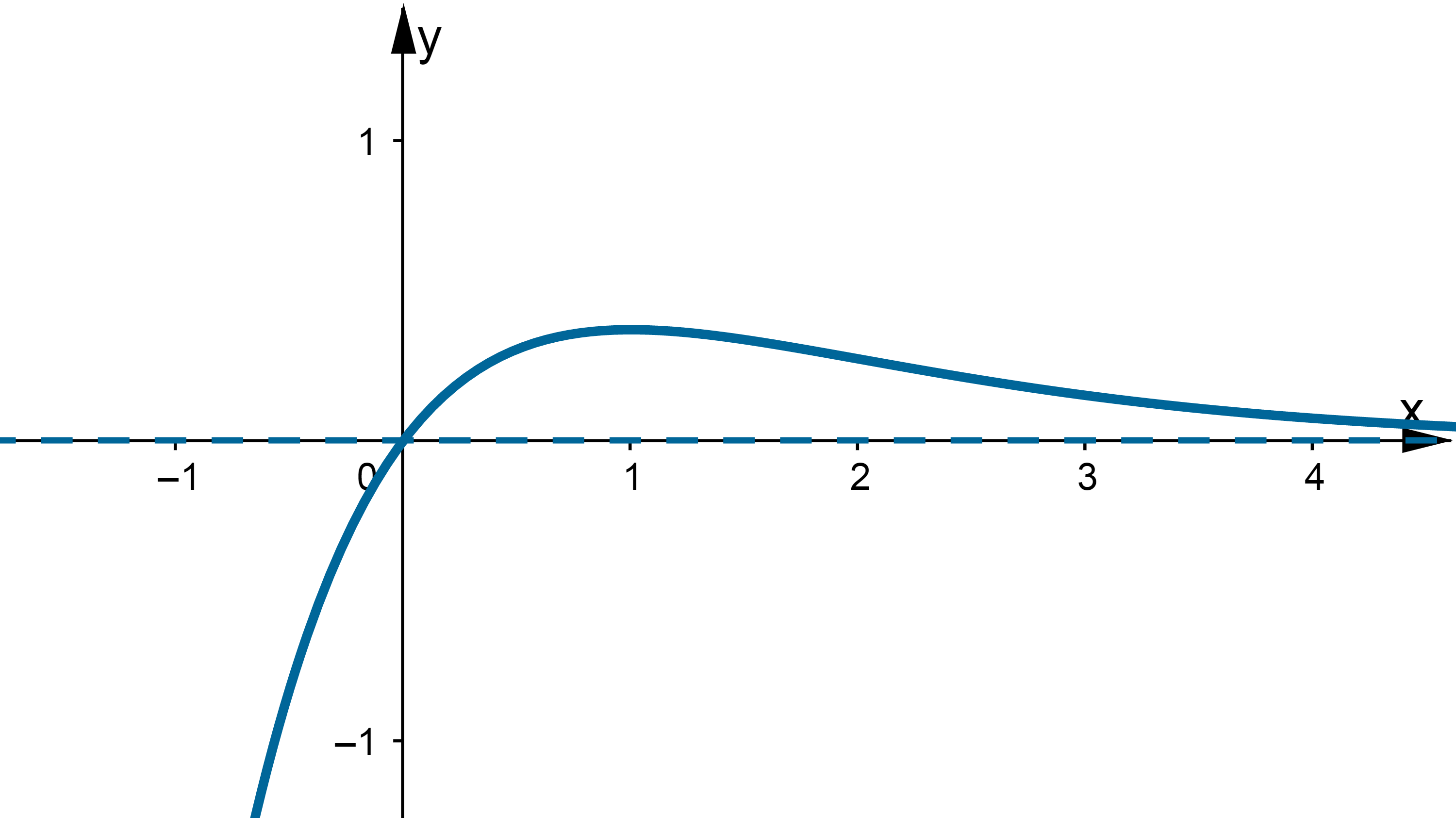
Wskazówka: Asymptotę pionową wykres funkcji może posiadać w punktach:
 ,
, 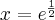 , asyptotę ukośną wykres funkcji może posiadać w
, asyptotę ukośną wykres funkcji może posiadać w 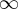 .
. 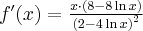 .
.
Odpowiedź: Dziedziną funkcji jest zbiór 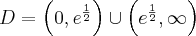 .
.
Funkcja ma asymptotę pionową obustronną 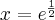 .
.
Funkcja jest rosnąca w każdym z przedziałów 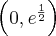 ,
,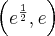 , malejąca w przedziale
, malejąca w przedziale 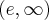 ,
,
w punkcie  funkcja ma maksimum lokalne,
funkcja ma maksimum lokalne, 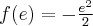 .
.