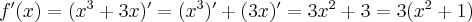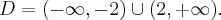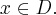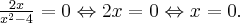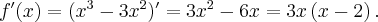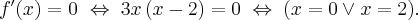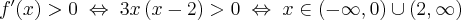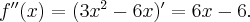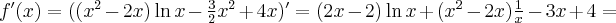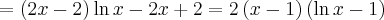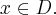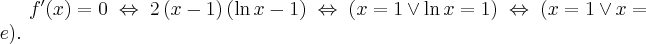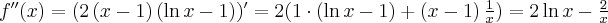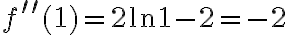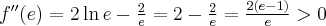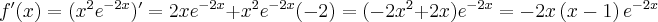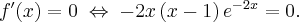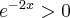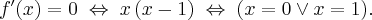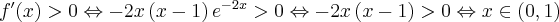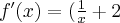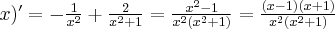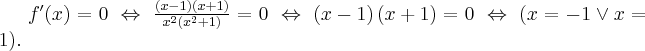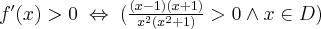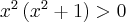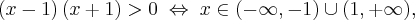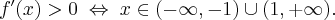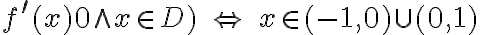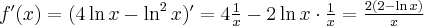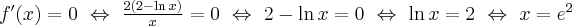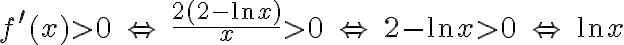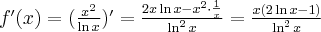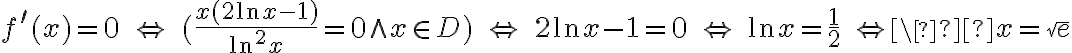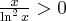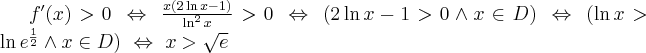3.2 Ekstrema lokalne funkcji (*)
Przykłady
Przykład 1
Wykażemy, że funkcja określona wzorem 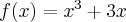 nie posiada ekstremów lokalnych.
nie posiada ekstremów lokalnych.
Funkcja  jest wielomianem, zatem dziedziną funkcji jest zbiór
jest wielomianem, zatem dziedziną funkcji jest zbiór 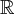 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
Ponieważ 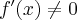 dla
dla  , więc
, więc  nie ma punktów stacjonarnych i w konsekwencji nie ma też ekstremów lokalnych (stosujemy wniosek z warunku koniecznego istnienia ekstremum lokalnego).
nie ma punktów stacjonarnych i w konsekwencji nie ma też ekstremów lokalnych (stosujemy wniosek z warunku koniecznego istnienia ekstremum lokalnego).
Przykład 2
Wykażemy, że funkcja określona wzorem 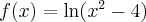 nie posiada ekstremów lokalnych.
nie posiada ekstremów lokalnych.
Obliczamy pochodną funkcji:
Wyznaczamy punkty stacjonarne funkcji  rozwiązując równanie:
rozwiązując równanie: 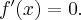
Jednakże 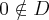 , zatem
, zatem  nie ma ekstremów lokalnych.
nie ma ekstremów lokalnych.
Przykład 3
Wyznaczymy ekstrema lokalne funkcji określonej wzorem 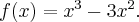
Zadanie rozpoczynamy od określenia dziedziny funkcji (w tym przypadku 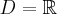 ) i zbadania, czy funkcja posiada punkty stacjonarne. Obliczamy pochodną funkcji
) i zbadania, czy funkcja posiada punkty stacjonarne. Obliczamy pochodną funkcji  :
:
Rozwiązujemy odpowiednie równanie:
Oba rozwiązania należą do dziedziny funkcji, a zatem  ma dwa punkty stacjonarne. Dalej rozstrzygamy o istnieniu ekstremów lokalnych w tych punktach stosując jedną z dwóch metod podanych poniżej.
ma dwa punkty stacjonarne. Dalej rozstrzygamy o istnieniu ekstremów lokalnych w tych punktach stosując jedną z dwóch metod podanych poniżej.
1 sposób (wykorzystujemy I warunek wystarczający istnienia ekstremum lokalnego)
Badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne:
 |
Stąd wynika, że 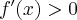 dla
dla 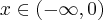 (a zatem także dla pewnego lewostronnego sąsiedztwa
(a zatem także dla pewnego lewostronnego sąsiedztwa  ) oraz
) oraz  dla
dla 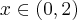 (przedział ten można potraktować jako prawostronne sąsiedztwo
(przedział ten można potraktować jako prawostronne sąsiedztwo  ). To oznacza, że
). To oznacza, że  ma w punkcie
ma w punkcie  maksimum lokalne
maksimum lokalne Pododnie
Pododnie  dla
dla 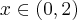 oraz
oraz 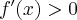 dla
dla 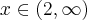 , czyli
, czyli  ma w punkcie
ma w punkcie  minimum lokalne.
minimum lokalne.
Metodę tę stosujemy najczęściej wtedy, gdy jednocześnie mamy wyznaczyć przedziały monotoniczności funkcji  .
.
2 sposób (wykorzystujemy II warunek wystarczający istnienia ekstremum lokalnego)
Obliczamy drugą pochodną funkcji  :
:
Ponieważ 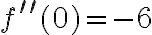 a zatem
a zatem  ma w punkcie
ma w punkcie  maksimum lokalne. Ponadto
maksimum lokalne. Ponadto 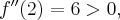 co oznacza, że
co oznacza, że  ma w punkcie
ma w punkcie  minimum lokalne.
minimum lokalne.
Ostatecznie stwierdzamy, że funkcja  posiada dwa ekstrema lokalne: maksimum lokalne w punkcie
posiada dwa ekstrema lokalne: maksimum lokalne w punkcie  o wartości
o wartości  oraz minimum lokalne w punkcie
oraz minimum lokalne w punkcie  o wartości
o wartości 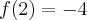 .
.
Przykład 4
Wyznaczymy ekstrema lokalne funkcji określonej wzorem 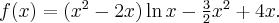
Funkcja  jest to przykładem funkcji, dla której szukając ekstremów lokalnych wygodniej jest stosować II warunek wystarczający.
jest to przykładem funkcji, dla której szukając ekstremów lokalnych wygodniej jest stosować II warunek wystarczający.
Dziedziną funkcji  jest zbiór
jest zbiór 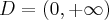 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  i zapisujemy ją w postaci iloczynowej:
i zapisujemy ją w postaci iloczynowej:
Wyznaczamy punkty stacjonarne funkcji  :
:
Dalej obliczamy drugą pochodną funkcji  :
:
Ponieważ
zatem  ma w punkcie
ma w punkcie 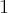 maksimum lokalne o wartości
maksimum lokalne o wartości 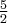 . Z kolei
. Z kolei
a zatem  ma w punkcie
ma w punkcie  minimum lokalne o wartości
minimum lokalne o wartości 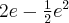 .
.
Przykład 5
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji określonej wzorem 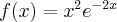 .
.
Na początek zauważmy, że 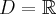 . Obliczamy pochodną funkcji i zapisujemy ją w postaci iloczynowej:
. Obliczamy pochodną funkcji i zapisujemy ją w postaci iloczynowej:
Wyznaczamy punkty stacjonarne funkcji  :
:
To oznacza, że funkcja  ma dwa punkty stacjonarne. Aby sprawdzić, czy
ma dwa punkty stacjonarne. Aby sprawdzić, czy  ma w nich ekstrema lokalne, zastosujemy I warunek wystarczający istnienia ekstremum lokalnego. W tym celu badamy, gdzie pochodna funkcji
ma w nich ekstrema lokalne, zastosujemy I warunek wystarczający istnienia ekstremum lokalnego. W tym celu badamy, gdzie pochodna funkcji  przyjmuje wartości dodatnie, a gdzie ujemne:
przyjmuje wartości dodatnie, a gdzie ujemne:

Stąd wynika, że istnieją sąsiedztwa 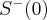 i
i 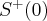 takie, że
takie, że 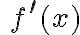 dla
dla 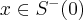 oraz
oraz 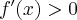 dla
dla 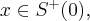 czyli
czyli  ma w
ma w  minimum lokalne. Podobnie uzasadniamy, że w
minimum lokalne. Podobnie uzasadniamy, że w 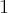 istnieje maksimum lokalne.
istnieje maksimum lokalne.
Uzyskane wyniki i odpowiedź (uwzględniając również przedziały monotoniczności badanej funkcji) najczęściej zapisujemy w postaci tabeli.
 |
 |
 |
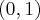 |
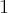 |
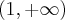 |
 |
 |
 |
 |
 |
 |
 |
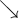 |
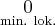 |
 |
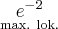 |
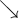 |
Przykład 6
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji określonej wzorem 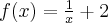 arctg
arctg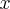 .
.
Na początek zauważmy, że 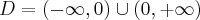 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
Wyznaczamy punkty stacjonarne funkcji  :
:
Następnie badamy, gdzie pochodna funkcji  przyjmuje wartości dodatnie, a gdzie ujemne:
przyjmuje wartości dodatnie, a gdzie ujemne:
więc ostatecznie
Analogicznie
Uzyskane wyniki zapisujemy w tabeli:
 |
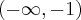 |
 |
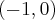 |
 |
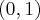 |
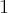 |
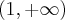 |
|
 |
 |
 |
 |
X |  |
 |
 |
|
 |
 |
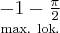 |
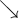 |
X | 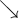 |
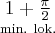 |
 |
Przykład 7
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji określonej wzorem 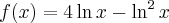 .
.
Na początek zauważmy, że 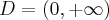 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
Wyznaczamy punkty stacjonarne funkcji  :
:
Jeśli 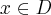 , to mianownik pierwszej pochodnej jest dodatni, a zatem
, to mianownik pierwszej pochodnej jest dodatni, a zatem
Analogicznie
Uzyskane wyniki zapisujemy w tabeli:
 |
 |
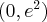 |
 |
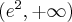 |
|
 |
X |  |
 |
 |
|
 |
X |  |
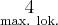 |
 |
Przykład 8
Wyznaczymy ekstrema lokalne i przedziały monotoniczności funkcji określonej wzorem 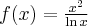 . Następnie naszkicujemy wykres funkcji
. Następnie naszkicujemy wykres funkcji  wiedząc dodatkowo, że
wiedząc dodatkowo, że 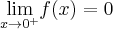 ,
, 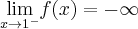 ,
, 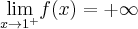 oraz
oraz 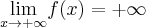 .
.
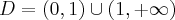 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
Wyznaczamy punkty stacjonarne funkcji  :
:
Uzyskane wyniki zapisujemy w tabeli:
 |
0 | 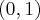 |
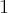 |
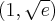 |
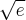 |
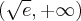 |
|
 |
X |  |
X |  |
 |
 |
|
 |
X | 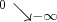 |
X | 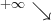 |
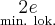 |
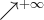 |
Na podstawie uzyskanych informacji szkicujemy wykres funkcji  :
:
obraz z wykresem