1.3 Interpretacja geometryczna pochodnej w punkcie
Ćwiczenia interaktywne
Przypomnij sobie:
• definicję stycznej do wykresu funkcji w punkcie • postać równania stycznej
Wyznacz równanie stycznej do wykresu funkcji  w punkcie
w punkcie  .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz równanie stycznej do wykresu funkcji  w punkcie
w punkcie 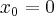 .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz równanie stycznej do wykresu funkcji  w punkcie
w punkcie  .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:
Wyznacz równanie stycznej do wykresu funkcji  w punkcie
w punkcie  .
.
Uzupełnij. Edycja tekstów w GeoGebrze
Rozwiązanie:



