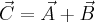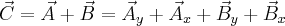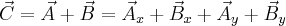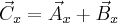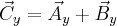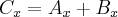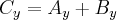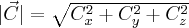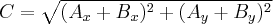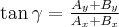Otrzymałeś dotąd 0 punktów z 0
Dodawanie wektorów z wykorzystaniem składowych - wyjaśnienie
Dodajemy wektory 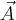 oraz
oraz 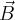 .
.
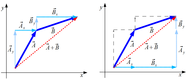
Etap 1
Każdy z wektorów 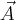 oraz
oraz 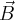 ) rozkładamy na składowe
) rozkładamy na składowe
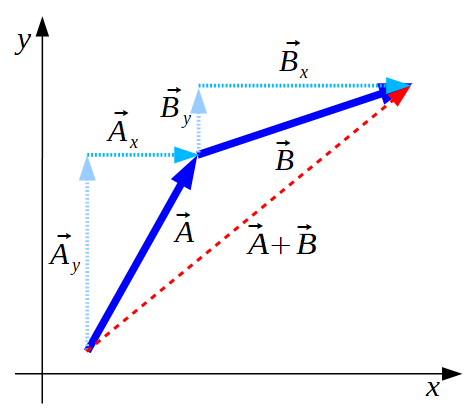
Teraz
Etap 2
Następnie korzystamy z przemienności dodawania
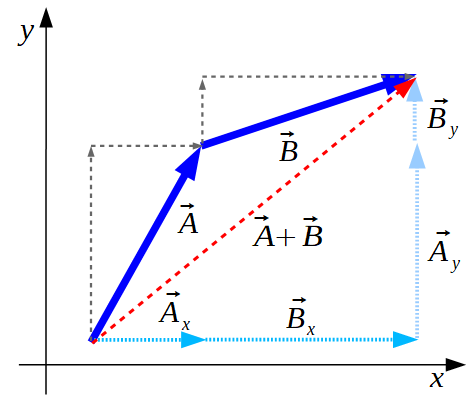
Teraz
Etap 3
Składowe 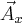 oraz
oraz 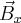 skierowane są wzdłuż osi
skierowane są wzdłuż osi  więc można je dodać dodając po prostu ich długości
więc można je dodać dodając po prostu ich długości
Podobnie postępujemy z wektorami 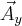 oraz
oraz 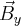 , które są równoległe do osi
, które są równoległe do osi  .
.
Etap 4
Długości składowych wektora 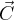 można policzyć w prosty sposób
można policzyć w prosty sposób
Etap 5
Korzystając z ogólnego równania na długość wektora
możemy znaleźć długość wektora 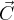 (w naszym wypadku dwuwymiarowego)
(w naszym wypadku dwuwymiarowego)
Etap 6
Możemy też znaleźć kąt 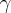 jaki wektor
jaki wektor 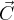 tworzy z osią
tworzy z osią 
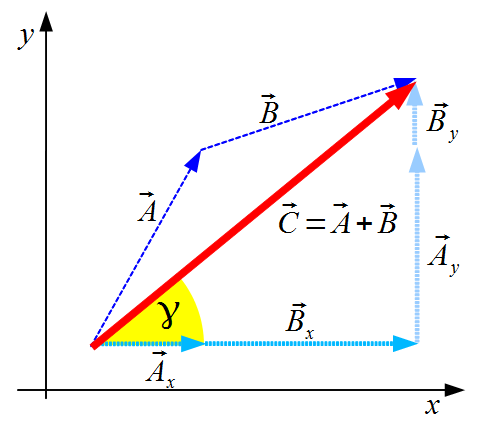
Procedura znajdowania kąta wektora 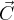 z osią
z osią  .
.