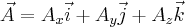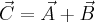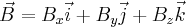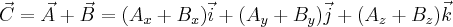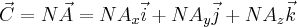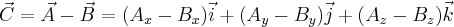Otrzymałeś dotąd 0 punktów z 0
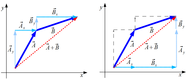
Dodawanie bez rysunku?
Korzystając z przedstawienia wektora jako suma składowych wyrażonych poprzez wektory jednostkowe
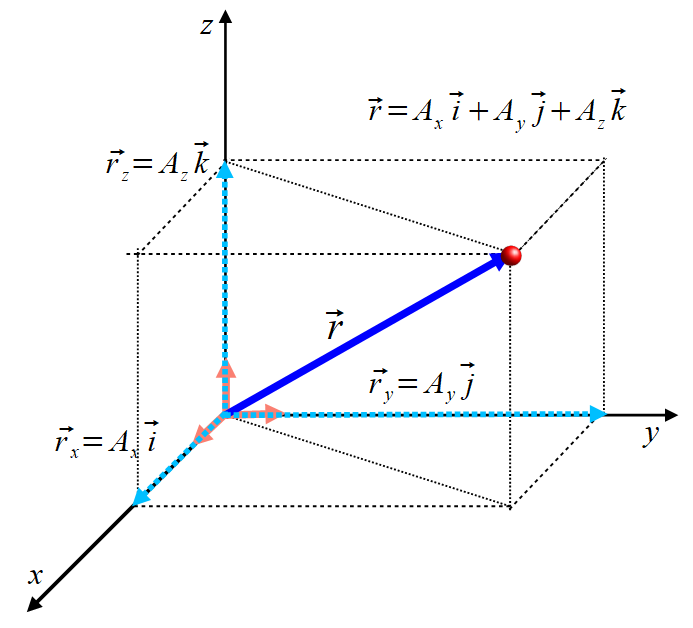
możemy dodawac wektory nawet ich nie widząc.
Chcemy znaleźć sumę
Jeśli wektor 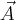 ma postać
ma postać
zaś wektor 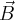
to
- suma wektorów
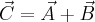 może być obliczona w następujący sposób
może być obliczona w następujący sposób
- natomiast mnożenie wektora przez liczbę ma teraz postać
- zaś odejmowanie