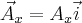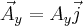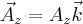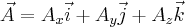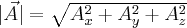Wektory - rozkład na składowe

Wiemy już, że każdą ze składowych wektora położenia możemy wyrazić jako iloczyn wektora jednostkowego (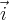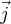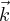$\vec{i}$, $\vec{j}$, $\vec{k}$) oraz liczby (z jednostką)

wersory

Resetuj rozmiar

Zamknij to okno

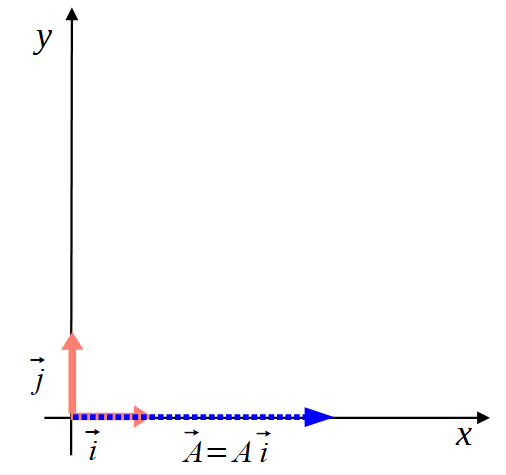
W takim razie możemy zapisać

• $\vec{A}_{x}=A_{x}\vec{i}$
• $\vec{A}_{y}=A_{y}\vec{j}$
• $\vec{A}_{z}=A_{z}\vec{k}$

a cały wektor można przedstawić w następujący sposób

$\vec{A}=A_{x}\vec{i}+A_{y}\vec{j}+A_{z}\vec{k}$

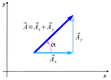
Tak to będzie wyglądało w dwóch wymiarach

wersory

Resetuj rozmiar

Zamknij to okno

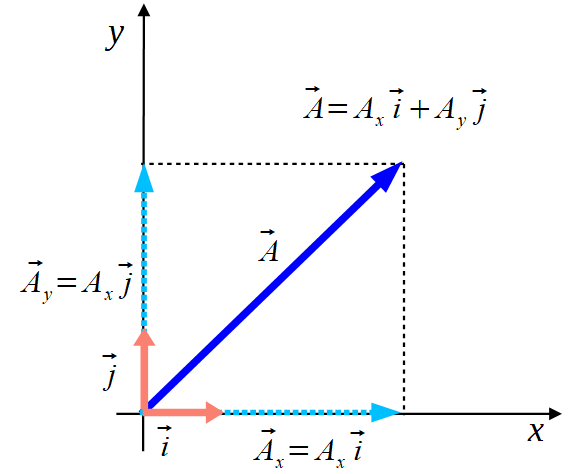
A tak w trzech wymiarach

wersory

Resetuj rozmiar

Zamknij to okno

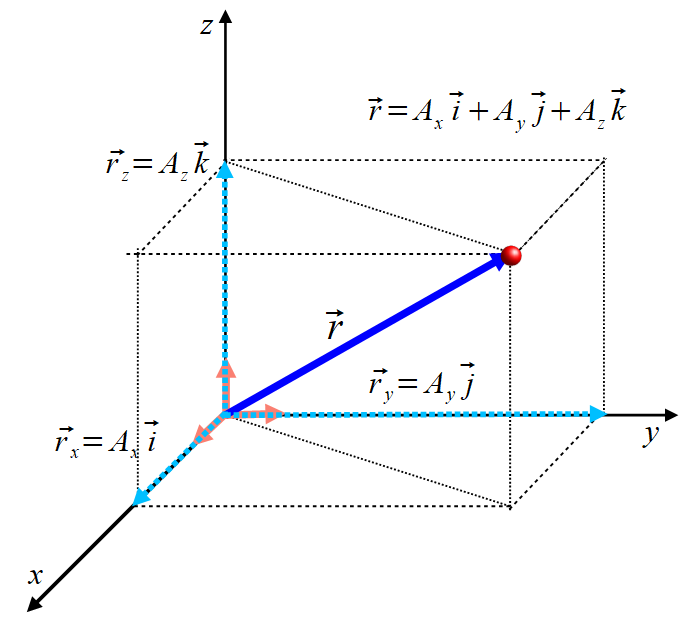
Przedstawienie wektora przy pomocy wersorów osi.

Długość wektora 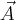$\vec{A}$ można obliczyć następująco

$|\vec{A}|=\sqrt{A_{x}^{2}+A_{y}^{2}+A_{z}^{2}}$