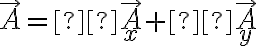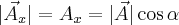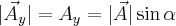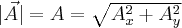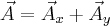Rozkład wektora na składowe
|
Wektor możemy przedstawić zawsze jako złożenie dwóch lub więcej tak zwanych wektorów składowych. |
Jeśli proces fizyczny opisujemy wykorzystując układ kartezjański dwuwymiarowy 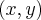 wtedy bardzo często przedstawiamy wektor
wtedy bardzo często przedstawiamy wektor 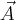 jako sumę dwóch wektorów:
jako sumę dwóch wektorów:
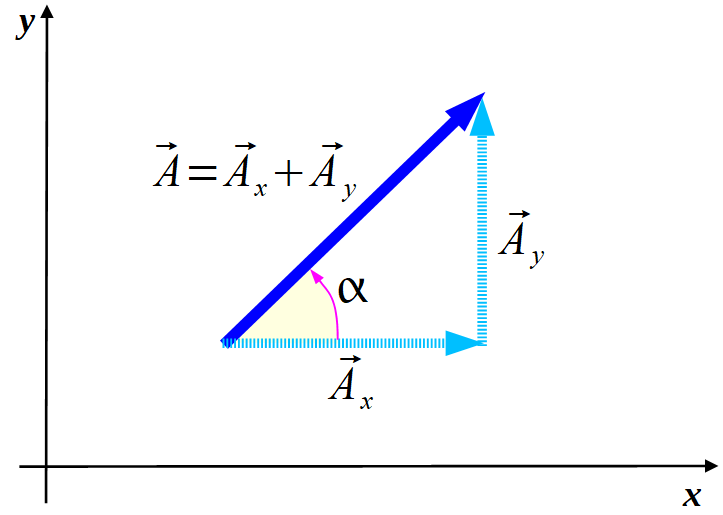
Spełniony jest warunek
Wektory 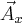 oraz
oraz 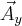 nazywamy składowymi wektora
nazywamy składowymi wektora 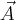 zaś sam proces nazywamy rozkładem wektora
zaś sam proces nazywamy rozkładem wektora 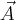 na składowe
na składowe
Długości wektorów składowych
Długości wektorów 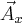 oraz
oraz 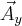 (oznaczane jako
(oznaczane jako 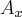 oraz
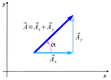
oraz 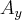 ) możemy znaleźć korzystając z funkcji trygonometrycznych dla trójkąta jaki widoczny jest na rysunku powyżej
) możemy znaleźć korzystając z funkcji trygonometrycznych dla trójkąta jaki widoczny jest na rysunku powyżej
Całkowita długość wektora
Długość wektora 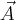 może być wyrażona poprzez długości wektorów
może być wyrażona poprzez długości wektorów 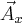 oraz
oraz 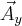 (twierdzenie Pitagorasa)
(twierdzenie Pitagorasa)
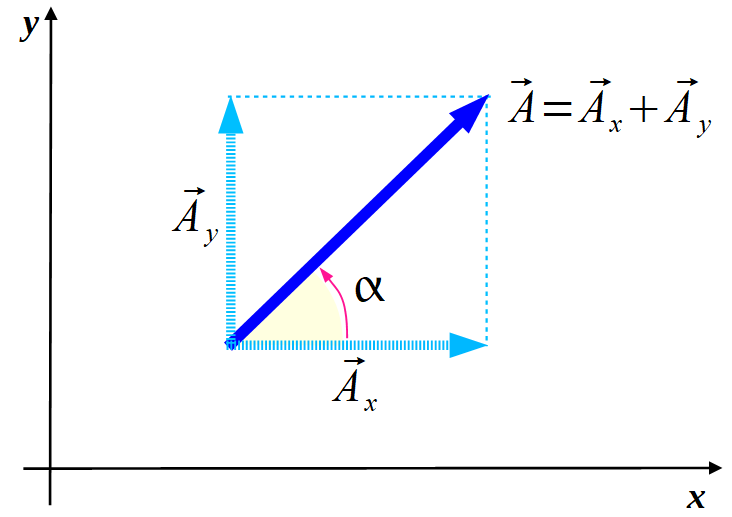
Rozkład wektora na składowe (wykorzystana reguła równoległoboku).