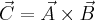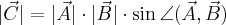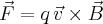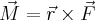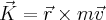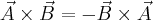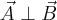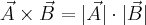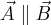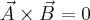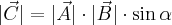Wektory - mnożenie

Wynikiem tego działania jest wektor

$\vec{C}=\vec{A}\times\vec{B}$

• Wartość (długość) wektora 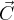$\vec{C}$ wynosi

$|\vec{C}|=|\vec{A}|\cdot|\vec{B}|\cdot\sin\angle(\vec{A},\vec{B})$

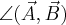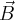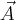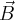
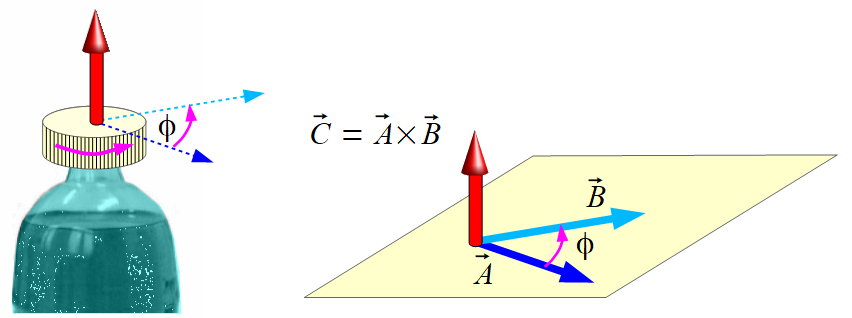
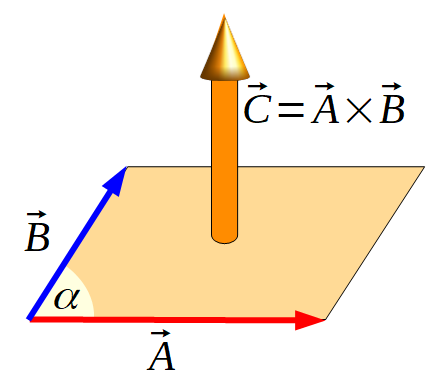
     gdzie $\angle(\vec{A},\vec{B})$ jest kątem pomiędzy wektorami $\vec{A}$ i $\vec{B}$ liczonym od wektora $\vec{A}$ do wektora $\vec{B}$ 

• Kierunek wektora $\vec{C}$ jest prostopadły do płaszczyzny zawierającej wektory $\vec{A}$ oraz $\vec{B}$

• Zwrot wektora $\vec{C}$ określa reguła śruby prawoskrętnej albo reguła nakrętki od butelki 

wektorowy

Resetuj rozmiar

Zamknij to okno

Definicja iloczynu wektorowego.

Pamiętaj, że kręcimy od pierwszego do drugiego wektora, po mniejszym kącie.

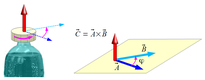
Kierunek wektrora 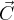$\vec{C}$ pokazuje pionowy ruch nakrętki od butelki.

Iloczyn wektorowy nie jest przemienny

$\vec{A}\times\vec{B}=-\vec{B}\times\vec{A}$

Zauważ także, że

• Jeśli $\vec{A}\perp\vec{B}$ to $\vec{A}\times\vec{B}=|\vec{A}|\cdot|\vec{B}|$
• Jeśli $\vec{A}\parallel\vec{B}$ to $\vec{A}\times\vec{B}=0$

Ciekawostka

Długość wektora 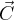$\vec C$ będącego iloczynek wektorowym 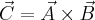$\vec C = \vec A \times \vec B$ wynosi

$|\vec{C}|=|\vec{A}|\cdot|\vec{B}|\cdot\sin\angle(\vec{A},\vec{B})$

czyli stosując oznaczenia z rysunku ponizej 

$|\vec{C}|=|\vec{A}|\cdot|\vec{B}|\cdot\sin \alpha$

Zauważ, że ta wielkość to jednoczesnie pole powierzchni równoległoboku widocznego poniżej

wektorowy

Resetuj rozmiar

Zamknij to okno