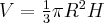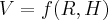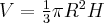Wprowadzenie
Po co pochodna cząstkowa?
Rozważmy przykładowy problem.
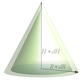
Jak wiadomo, objętość stożka  (rysunek poniżej) można policzyć z wzoru
(rysunek poniżej) można policzyć z wzoru
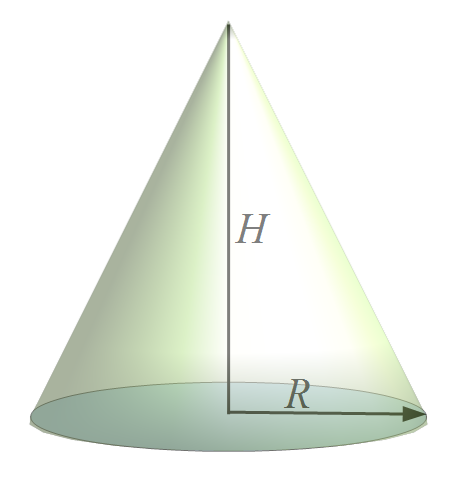
Objętość  jest więc funkcją dwóch zmiennych:
jest więc funkcją dwóch zmiennych:
Jeśli więc zmienimy promień podstawy 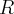 albo zmienimy wysokość stożka
albo zmienimy wysokość stożka  wtedy objętość stożka zmieni się.
wtedy objętość stożka zmieni się.
Chcemy się dowiedzieć jak zmiana poszczególnych wymiarów stożka wpłynie na jego objętość.
Patrząc na wzór
łatwo zauważyć, że gdy zwiększymy promień podstawy 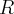 to objętość stożka \(\) wzrośnie. Analogicznie, gdy zwiększymy wysokość stożka
to objętość stożka \(\) wzrośnie. Analogicznie, gdy zwiększymy wysokość stożka  wtedy objętość stożka
wtedy objętość stożka  także wzrośnie.
także wzrośnie.
Ale nie zawsze odpowiedź będzie taka prosta. Na przykład:
- Czy wzrost objętości
 będzie większy gdy promień podstawy
będzie większy gdy promień podstawy 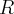 zwiększymy o 10 % czy też wtedy gdy o 10 % zwiększymy wysokość
zwiększymy o 10 % czy też wtedy gdy o 10 % zwiększymy wysokość  ?
? - Co się stanie z objętością stożka
 gdy promień podstawy
gdy promień podstawy 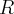 zwiększymy o 10 % zaś wysokość
zwiększymy o 10 % zaś wysokość  zmniejszymy o 10 % ?
zmniejszymy o 10 % ?
Oczywiście, w konkretnych przypadkach możemy podstawić liczby i to sprawdzić. Ale co, jeśli chcemy uzyskać odpowiedź bardziej ogólną?
Wiemy już, że narzędziem, które pozwala na opisanie jak jedna wielkość wpływa na drugą wielkość jest pochodna. Na przykład szybkość zmian prędkości samochodu w zależności od czasu opisuje pierwsza pochodna prędkości po czasie 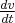 .
.
Także w przypadku opisywanego stożka wykorzystać możemy pochodną, ale tym razem mamy problem, jak to zrobić kiedy wielkość zależy od większej ilości parametrów, czyli jest funkcją wielu zmiennych.
Do tego właśnie służy pochodna cząstkowa 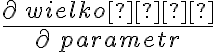 którą omówimy w następnych krokach.
którą omówimy w następnych krokach.