Zasada Fermata - prawo odbicia
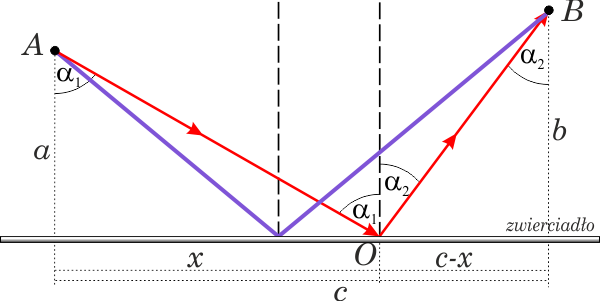
Weźmy pod uwagę dowolny promień (oznaczony kolorem czerwonym). Niech odbije się od zwierciadła w punkcie \(O\). Czas w jakim pokona drogę \(AOB\) wyraźmy poprzez długości odcinków \(a\), \(b\), \(c\) oraz \(x\). Prędkość rozchodzenia się fali w ośrodku \(v\).
\(\Large{t=\frac{\overline{AO}}{v}+\frac{\overline{OB}}{v}=\frac{\sqrt{a^2+x^2}}{v}+\frac{\sqrt{b^2+(c-x)^2}}{v}}\)
Szukamy teraz minimalnego czasu. Musimy więc policzyć pochodną czasu po \(\Large{x}\) i przyrównać ją do zera.
\(\Large{\frac{dt}{dx}=\frac{x}{v\sqrt{a^2+x^2}}-\frac{c-x}{v\sqrt{b^2+(c-x)^2}}=\frac{\sin{\alpha_1}}{v}-\frac{\sin{\alpha_2}}{v}=0}\)
a stąd wynika, że:
\(\Large{\frac{\sin{\alpha_1}}{v}=\frac{\sin{\alpha_2}}{v}}\)
czyli
\(\Large{\sin{\alpha_1}=\sin{\alpha_2}}\)
a stąd
\(\Large{\alpha_1=\alpha_2}\)
Otrzymaliśmy więc prawo odbicia - kąt padania jest równy kątowi odbicia.
