Zjawisko całkowitego wewnętrznego odbicia
Rysunek poniżej przedstawia sytuację gdy fala porusza się w ośrodku w którym ma mniejszą prędkość (większy współczynnik załamania) w stronę granicy z ośrodkiem w którym fala rozchodzi się z większa prędkością (współczynnik załamania mniejszy). Może to być dla przykładu źródło światła (fala elektromagnetyczna) umieszczone pod wodą.
Promienie docierające do granicy ośrodków ulegają częściowemu odbiciu i załamaniu. Wraz ze wzrostem kąta padania \(\varphi\) (kolejno promień czarny, pomarańczowy \(\varphi_1\), zielony \(\varphi_2\)) natężenie światła odbijanego wzrasta, a światła załamanego maleje. W końcu, gdy kąt załamania osiąga 90o (promień fioletowy) wiązka załamana osiąga zerowe natężenie (nie istnieje) - światło porusza się wzdłuż granicy ośrodków. Kąt padania dla którego zachodzi to zjawisko to tzw. kąt graniczny \(\varphi_{gr}\).
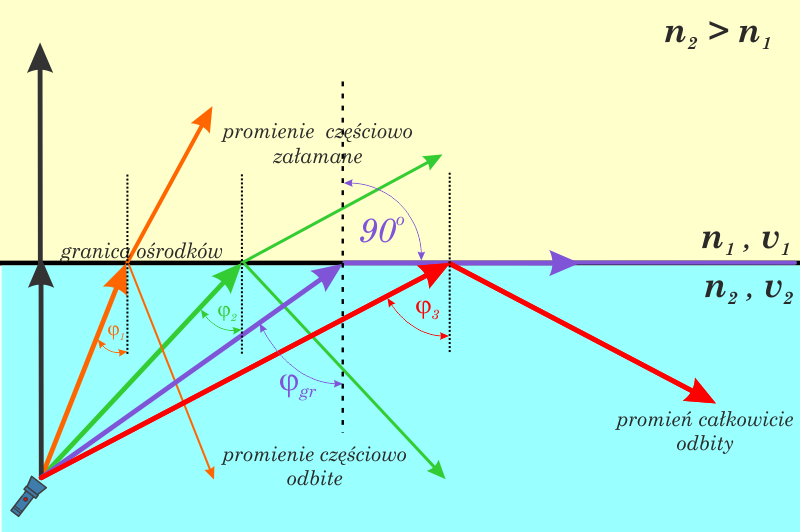
\(\Large{\varphi_{gr}}\)– kąt graniczny
\(\Large{n_1}\) – współczynnik załamania ośrodka 1.
\(\Large{n_2}\) – współczynnik załamania ośrodka 2.
Dla kąta granicznego \(\Large{\varphi_{gr}}\) kąt załamania wynosi \(90^o\).
Dla kątów padania większych od \(\Large{\varphi_{gr}}\) promień pozostaje wewnątrz ośrodka (promień czerwony, \(\Large{\varphi_3}\)>\(\Large{\varphi_{gr}}\)) i odbija się zgodnie z prawem odbicia, czyli kąt padania jest równy kątowi odbicia. Jest to zjawisko całkowitego wewnętrznego odbicia. Co istotne w przypadku całkowitego wewnętrznego odbicia nie ma strat natężenia przy odbiciu. Stąd szereg zastosowań tego zjawiska o których przeczytasz na kolejnych slajdach.
Można oczywiście określić warunek matematyczny na kąt graniczny. Z prawa załamania (prawa Snelliusa):
\(\Large{\frac{\sin{\varphi_{gr}}}{\sin{90^o}}=\frac{n_1}{n_2}}\)
czyli
\(\Large{\sin{\varphi_{gr}}=\frac{n_1}{n_2}}\)
