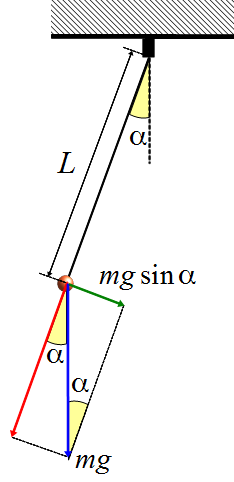
Można pokazać, że równanie ruchu dla takiego wahadła ma postać:
\( \frac{d^{2}\alpha}{\mathit{dt}^{2}}=-\mathit{\frac{g}{L}}\sin\alpha \)To NIE JEST ruch harmoniczny prosty ponieważ przyspieszenie kątowe \( \frac{d^{2}\alpha}{\mathit{dt}^{2}}\) NIE JEST proporcjonalne do wychylenia (kąta \(\alpha\)).
Rozwiązanie równania powyżej stanowi pewne wyzwanie matematyczne. W skrócie można powiedzieć, że rozwiązanie opisuje ruch drgający, który nie jest ruchem harmonicznym.
Okres drgań wahadła opisywany jest przez skomplikowaną funkcję
\(T=2\pi\sqrt{\frac{l}{g}}\left[1+\left(\frac{1}{2}\right)^{2}\sin^{2}\left(\frac{1}{2}\alpha_{m}\right)+\left(\frac{1\cdot3}{2\cdot4}\right)^{2}\sin^{4}\left(\frac{1}{2}\alpha_{m}\right)+\left(\frac{1\cdot3\cdot5}{2\cdot4\cdot6}\right)^{2}\sin^{6}\left(\frac{1}{2}\alpha_{m}\right)+\ldots\right]\)
gdzie \(\alpha_{m}\) jest amplitudą (maksymalnym kątem).
Jak widać okres drgań \(T\) zależy od amplitudy.
Jeśli jednak ograniczymy się do małych kątów (małych amplitud) wtedy można zastosować przybliżenie
\( \sin\alpha\approx\alpha\)I równanie ruchu wahadła staje się znacznie prostsze
\(\frac{d^{2}\alpha}{\mathit{dt}^{2}}=-\frac{g}{L}\alpha\)Teraz jest to równanie ruchu harmonicznego prostego
Okres drgań \(T\) wynosi teraz:
\(T=2\pi\sqrt{\frac{L}{g}}\)
Pamiętaj, że przybliżenie \(\sin\alpha=\alpha\) jest prawdziwe tylko dla "małych kątów". Nie można precyzyjnie określić jaki kąt jest mały. Zależy to od oczekiwanej dokładności rozwiązania.
Można jednak powiedzieć, że uproszczony wzór nie jest prawdziwy dla dużych amplitud.
Symulacja
Symulacja poniżej pozwala porównać drgania wahadła matematycznego dla różnych amplitud.
Mamy dwa wahadła. Jedno wykonuje drgania o małej amplitudzie. Amplitudę drugiego możesz ustawić samodzielnie (może być duża). Można także obserwować wpływ siły oporu na każde z wahadeł.
Na wykresach obserwować można zmiany wychylenia w czasie dla obu wahadeł oraz ich portrety fazowe (zależność prędkości od wychylenia). .
