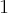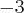Nawigacja
Menu strony głównej
- Portal Informacyjny PŁ
- Studia podyplomowe BAIŚ
- Studia podyplomowe BINOŻ
- Studia podyplomowe FTIMS
- Studia podyplomowe OIZ
- Studia podyplomowe TMiWT
- Studia podyplomowe WEEIA
- Studia podyplomowe WIPOŚ
- Otwarte zasoby edukacyjne Politechniki Łódzkiej
- Zasoby zdalne
- Centrum Językowe PŁ
- Konkurs Matematyczny im. prof. W. Krysickiego
- CMF
- Centrum Kształcenia Międzynarodowego
- Studia podyplomowe CPP
- Studia podyplomowe CHEMIA
- ECIU
Wirtualne Wydziały
virTUL
Skróty klawiszowe
Ctrl
+Alt
+F
Otwórz/zamknij menu główne i przejdź do wyszukiwania pozycji w menu.
Ctrl
+Alt
+H
Otwórz/zamknij menu główne i przejdź do wyszukiwania przedmiotu.
Ctrl
+Alt
+M
Otwórz/zamknij menu użytkownika.
Ctrl
+Alt
+→
Wysuń menu nawigacji po portalu.
Ctrl
+Alt
+←
Ukryj menu nawigacji po portalu.
Tab
Przejdź do następnej pozycji w menu głównym.
Shift
+Tab
Przejdź do poprzedniej pozycji w menu głównym.
Enter
Wybierz wyróżnioną pozycję w menu głównym (przekierowanie do wybranej lokalizacji).
Esc
Zamknij/zwiń aktywne menu.
Rachunek różniczkowy funkcji jednej zmiennej
Wymagania zaliczenia


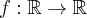


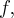
![[-5, 4] [-5, 4]](https://port.edu.p.lodz.pl/filter/tex/pix.php/c1c70481fe548642a4a88044d86f065d.png)
![[-3, 1] [-3, 1]](https://port.edu.p.lodz.pl/filter/tex/pix.php/d2df8b17485bbc7266d72fd130f949fe.png)