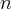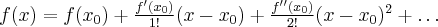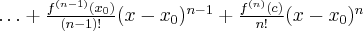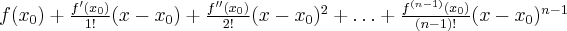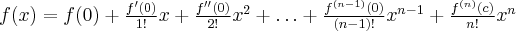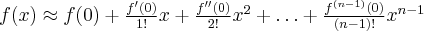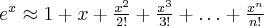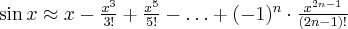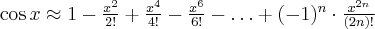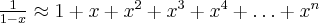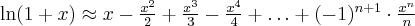2.2 Twierdzenie Taylora
Teoria
Taylora
Powyższy wzór nazywany jest wzorem Taylora, zaś wyrażenie 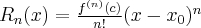 resztą Taylora w postaci Lagrange'a. Wielomian postaci
resztą Taylora w postaci Lagrange'a. Wielomian postaci
nazywamy wielomianem Taylora stopnia  w punkcie
w punkcie  .
.
Jeżeli  , to wzór Taylora ma postać
, to wzór Taylora ma postać
i nazywany jest wzorem Maclaurina (punkt  leży pomiędzy
leży pomiędzy  i
i  ). Pomijając w powyższym wzorze resztę Taylora
). Pomijając w powyższym wzorze resztę Taylora 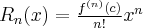 , otrzymujemy przybliżenie (aproksymację) funkcji
, otrzymujemy przybliżenie (aproksymację) funkcji  za pomocą wielomianu Maclaurina:
za pomocą wielomianu Maclaurina:
przy czym błąd bezwzględny tego przybliżenia wynosi 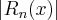 . Jeżeli wszystkie pochodne funkcji
. Jeżeli wszystkie pochodne funkcji  są wspólnie ograniczone, to
są wspólnie ograniczone, to 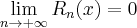 . Wówczas możemy obliczyć wartość funkcji
. Wówczas możemy obliczyć wartość funkcji  z dowolną dokładnością.
z dowolną dokładnością.
Przybliżenie wybranych funkcji za pomocą wzoru Maclaurina: