1.3 Interpretacja geometryczna pochodnej w punkcie
Teoria

Iloraz różnicowy 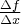 równy jest tangensowi kąta
równy jest tangensowi kąta  nachylenia prostej (siecznej) przechodzącej przez punkty
nachylenia prostej (siecznej) przechodzącej przez punkty  i
i  :
:
Jeżeli granica  istnieje i jest skończona, to jej wartość równa jest tangensowi kąta
istnieje i jest skończona, to jej wartość równa jest tangensowi kąta  nachylenia stycznej do wykresu funkcji
nachylenia stycznej do wykresu funkcji  poprowadzonej w punkcie
poprowadzonej w punkcie  , zatem
, zatem

Pochodna  jest równa współczynnikowi kierunkowemu stycznej do wykresu funkcji
jest równa współczynnikowi kierunkowemu stycznej do wykresu funkcji  poprowadzonej w punkcie
poprowadzonej w punkcie  .
.








