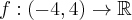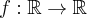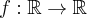4.2 Ekstrema lokalne funkcji
Ćwiczenia interaktywne, cz.1
Przypomnij sobie:
• definicje ekstremów lokalnych • warunek konieczny istnienia ekstremum lokalnego • I warunek wystarczający istnienia ekstremum lokalnego • II warunek wystarczający istnienia ekstremum lokalnego
1
2
Przyporządkuj podane funkcje do odpowiedniej grupy.
Przeciągnij poprawne odpowiedzi w odpowiednie pola.
3
4
5
6
7
8
9
Czy funkcja  posiada ekstrema lokalne we wskazanych punktach? Uzasadnij odpowiedź.
posiada ekstrema lokalne we wskazanych punktach? Uzasadnij odpowiedź.
Uzupełnij.
10
Czy funkcja  posiada ekstrema lokalne we wskazanych punktach? Uzasadnij odpowiedź.
posiada ekstrema lokalne we wskazanych punktach? Uzasadnij odpowiedź.
Uzupełnij.