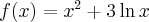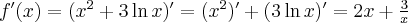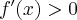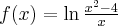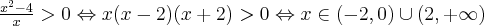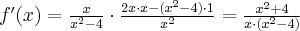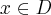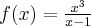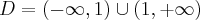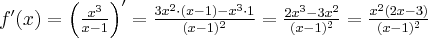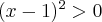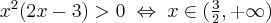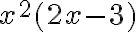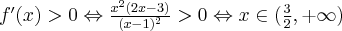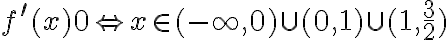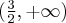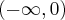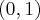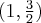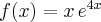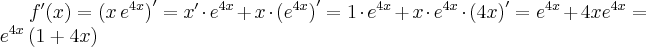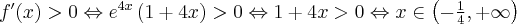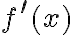4.1 Badanie monotoniczności funkcji
Przykłady
Aby wyznaczyć dziedzinę funkcji  należy rozwiązać nierówność
należy rozwiązać nierówność 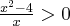 . Ponieważ
. Ponieważ
zatem 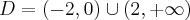 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
Zauważamy, że pochodna funkcji jest dodatnia w całej dziedzinie. Nie oznacza to jednak, że funkcja jest rosnąca w całej dziedzinie, gdyż dziedzina nie jest przedziałem a sumą przedziałów. A zatem stwierdzamy, że funkcja  jest rosnąca na przedziale
jest rosnąca na przedziale 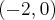 i na przedziale
i na przedziale  .
.
Dziedziną funkcji jest zbiór 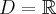 . Obliczamy pochodną funkcji:
. Obliczamy pochodną funkcji:
Aby wyznaczyć przedziały monotoniczności funkcji  badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Ponieważ
badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Ponieważ 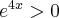 dla każdego
dla każdego  więc
więc
Zatem badana funkcja jest rosnąca na przedziale 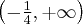 oraz malejąca na przedziale
oraz malejąca na przedziale 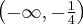 .
.
Z uwagi 2 wynika, że funkcja  jest również monotoniczna na przedziałach domkniętych, tzn. rosnąca na przedziale
jest również monotoniczna na przedziałach domkniętych, tzn. rosnąca na przedziale 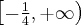 oraz malejąca na przedziale
oraz malejąca na przedziale ![\left(-\infty, -\frac14\right] \left(-\infty, -\frac14\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/05f7716a9abeb6d2ce9ac2ef90409b4c.png) – są to maksymalne przedziały monotoniczności funkcji
– są to maksymalne przedziały monotoniczności funkcji  .
.