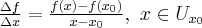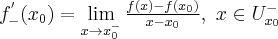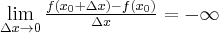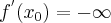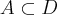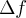1.1 Pochodna funkcji w punkcie
Teoria
Załóżmy, że funkcja  jest określona na pewnym otoczeniu
jest określona na pewnym otoczeniu  punktu
punktu  . Niech
. Niech  będzie różnym od zera przyrostem zmiennej
będzie różnym od zera przyrostem zmiennej  takim, że
takim, że  należy do tego otoczenia. Niech
należy do tego otoczenia. Niech  będzie przyrostem wartości funkcji odpowiadającym przyrostowi
będzie przyrostem wartości funkcji odpowiadającym przyrostowi  . Ilorazem różnicowym funkcji
. Ilorazem różnicowym funkcji  w punkcie
w punkcie  dla przyrostu
dla przyrostu  nazywamy wyrażenie
nazywamy wyrażenie
Jeżeli istnieje i jest skończona granica
to nazywamy ją pochodną funkcji  w punkcie
w punkcie  i oznaczamy
i oznaczamy  lub
lub  . Zatem
. Zatem
(o ile granica ta istnieje i jest skończona).
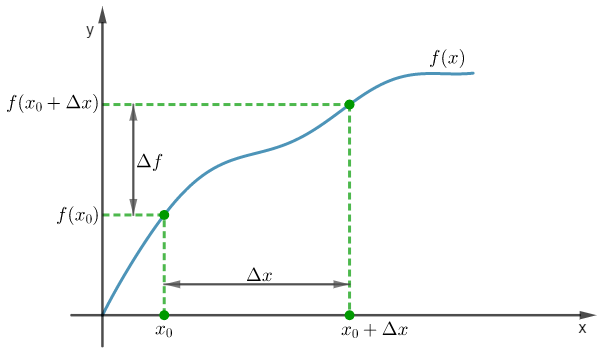
Funkcję jednej zmiennej, która ma pochodną w punkcie  nazywamy funkcją różniczkowalną w tym punkcie.
nazywamy funkcją różniczkowalną w tym punkcie.
Załóżmy, że funkcja  jest określona na pewnym prawostronnym otoczeniu
jest określona na pewnym prawostronnym otoczeniu  . Niech
. Niech  będzie różnym od zera przyrostem zmiennej
będzie różnym od zera przyrostem zmiennej  takim, że
takim, że  należy do tego otoczenia. Niech
należy do tego otoczenia. Niech  będzie przyrostem funkcji odpowiadającym przyrostowi
będzie przyrostem funkcji odpowiadającym przyrostowi  . Jeżeli istnieje i jest skończona granica
. Jeżeli istnieje i jest skończona granica
to nazywamy ją pochodną prawostronną funkcji  w punkcie
w punkcie  i oznaczamy
i oznaczamy 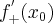 lub
lub  . Zatem
. Zatem
Załóżmy, że funkcja  jest określona na pewnym lewostronnym otoczeniu
jest określona na pewnym lewostronnym otoczeniu  . Niech
. Niech  będzie różnym od zera przyrostem zmiennej
będzie różnym od zera przyrostem zmiennej  takim, że
takim, że  należy do tego otoczenia. Niech
należy do tego otoczenia. Niech  będzie przyrostem funkcji odpowiadającym przyrostowi
będzie przyrostem funkcji odpowiadającym przyrostowi  . Jeżeli istnieje i jest skończona granica
. Jeżeli istnieje i jest skończona granica
to nazywamy ją pochodną lewostronną funkcji  w punkcie
w punkcie  i oznaczamy
i oznaczamy  . Zatem
. Zatem