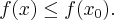4.2 Ekstrema lokalne funkcji (*)
Teoria
Mówimy, że funkcja  ma w punkcie
ma w punkcie  maksimum lokalne, jeżeli istnieje zawarte w dziedzinie funkcji
maksimum lokalne, jeżeli istnieje zawarte w dziedzinie funkcji  otoczenie
otoczenie  punktu
punktu  takie, że dla wszystkich
takie, że dla wszystkich 
Mówimy, że funkcja  ma w punkcie
ma w punkcie  minimum lokalne, jeżeli istnieje zawarte w dziedzinie funkcji
minimum lokalne, jeżeli istnieje zawarte w dziedzinie funkcji  otoczenie
otoczenie  punktu
punktu  takie, że dla wszystkich
takie, że dla wszystkich 
Jeżeli dla każdego  zachodzi nierówność
zachodzi nierówność 
 , to mówimy o maksimum (minimum) lokalnym właściwym.
, to mówimy o maksimum (minimum) lokalnym właściwym.
Jeżeli funkcja  jest różniczkowalna w punkcie
jest różniczkowalna w punkcie  i ma w tym punkcie ekstremum lokalne, to
i ma w tym punkcie ekstremum lokalne, to 
Funkcja może mieć ekstremum lokalne jedynie w punkcie  , takim że
, takim że  (gdy jest różniczkowalna w
(gdy jest różniczkowalna w  ) lub w punkcie
) lub w punkcie  , w którym funkcja
, w którym funkcja  nie ma pochodnej.
nie ma pochodnej.
Punkty, w których pochodna funkcji zeruje się nazywamy punktami stacjonarnymi tej funkcji.
Jeżeli funkcja  jest ciągła na pewnym otoczeniu
jest ciągła na pewnym otoczeniu  i różniczkowalna na sąsiedztwie
i różniczkowalna na sąsiedztwie  punktu
punktu  oraz
oraz
lub
to funkcja  ma w punkcie
ma w punkcie  ekstremum lokalne właściwe. Jest to maksimum lokalne w przypadku 1, minimum lokalne gdy zachodzi warunek 2.
ekstremum lokalne właściwe. Jest to maksimum lokalne w przypadku 1, minimum lokalne gdy zachodzi warunek 2.
Jeżeli funkcja  jest dwukrotnie różniczkowalna na pewnym otoczeniu punktu
jest dwukrotnie różniczkowalna na pewnym otoczeniu punktu  oraz
oraz
to funkcja  ma w punkcie
ma w punkcie  ekstremum lokalne właściwe, przy czym jest to maksimum lokalne, jeżeli
ekstremum lokalne właściwe, przy czym jest to maksimum lokalne, jeżeli  , minimum lokalne, gdy
, minimum lokalne, gdy  .
.