3. Reguła de l'Hospitala
Przykłady
1
Obliczymy granice funkcji stosując regułę de l'Hospitala:
- Zaczynamy od określenia symbolu granicy, aby zdecydować, czy można zastosować regułę de l'Hospitala. Następnie badamy, czy istnieje granica ilorazu pochodnych: Na mocy reguły de l'Hospitala otrzymujemy odpowiedź
- Zwykle stosując regułę de l'Hospitala stosujemy uproszczony zapis przedstawiony poniżej.
- Określamy symbol badanej granicy: Symbol granicy jest oznaczony, a zatem w tym przypadku nie można wykorzystać reguły de l'Hospitala. Aby obliczyć granicę należy zastosować odpowiednie twierdzenia arytmetyki granic funkcji: Na koniec zauważmy, że w tym przypadku a zatem granica ilorazu pochodnych różni się od badanej granicy. Przykład ten pokazuje, iż stosowanie reguły de l'Hospitala bez sprawdzenia założeń tego twierdzenia może prowadzić do błędnej odpowiedzi.
2
Obliczymy granice funkcji stosując regułę de l'Hospitala:
- Obliczymy podaną granicę funkcji stosując regułę de l'Hospitala:
- W przypadku tej granicy regułę de l'Hospitala zastosujemy dwukrotnie:
- Obliczymy podaną granicę funkcji stosując regułę de l'Hospitala i wykorzystując fakt, że
 .
.
3
- Podobnie jak w poprzednich przykładach zaczynamy od określenia symbolu badanej granicy
przy czym
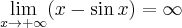 na mocy twierdzenia o dwóch funkcjach. W tym przypadku nie możemy wykorzystać reguły de l'Hospitala, gdyż
zaś taka granica nie istnieje. Nie oznacza to jednak, że nie istnieje badana granica – trzeba tylko policzyć ją innym sposobem. Ponieważ
oraz
na mocy twierdzenia o dwóch funkcjach. W tym przypadku nie możemy wykorzystać reguły de l'Hospitala, gdyż
zaś taka granica nie istnieje. Nie oznacza to jednak, że nie istnieje badana granica – trzeba tylko policzyć ją innym sposobem. Ponieważ
oraz  , więc na mocy twierdzenia o trzech funkcjach
, więc na mocy twierdzenia o trzech funkcjach 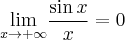 . Stąd
. Stąd
- W tym przypadku a zatem stosowanie reguły de l'Hospitala nie jest efektywne. Granicę funkcji możemy jednak obliczyć w inny sposób:
4
- Zaczynamy od określenia symbolu badanej granicy funkcji:
W tym przypadku, aby zastosować regułę de l'Hospitala, wyrażenie
 zapiszemy w postaci ilorazu
zapiszemy w postaci ilorazu  . Dwukrotnie stosując regułę de l'Hospitala otrzymujemy:
. Dwukrotnie stosując regułę de l'Hospitala otrzymujemy:
- Podobnie jak poprzednim przykładzie określimy najpierw symbol badanej granicy funkcji:
Następnie przekształcimy funkcję, której granicę obliczamy, w taki sposób by można było zastosować regułę de l'Hospitala. A zatem
- Ustalimy najpierw symbol badanej granicy funkcji:
Przekształcimy funkcję stosując tożsamość:
 . A zatem
. A zatem
Korzystając z wyniku otrzymanego w podpunkcie (b) mamy
5
Zauważmy, że dla wszystkich rozważanych w tym przykładzie granic otrzymujemy symbole nieoznaczone ![\left[\infty-\infty\right] \left[\infty-\infty\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/0a4382dc250cc70672eb67f35df398fa.png) , które po odpowiednich przekształceniach sprowadzimy do symbolu
, które po odpowiednich przekształceniach sprowadzimy do symbolu ![\left[ \frac{\infty}{\infty} \right] \left[ \frac{\infty}{\infty} \right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/de5999aa6f0b4ca90cab98e7c03f31a2.png) albo
albo ![\left[ \frac{0}{0} \right] \left[ \frac{0}{0} \right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/8e3f348a630785530b38a36fe9e9c071.png) .
.
![\left[\infty-\infty\right] \left[\infty-\infty\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/0a4382dc250cc70672eb67f35df398fa.png) , które po odpowiednich przekształceniach sprowadzimy do symbolu
, które po odpowiednich przekształceniach sprowadzimy do symbolu ![\left[ \frac{\infty}{\infty} \right] \left[ \frac{\infty}{\infty} \right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/de5999aa6f0b4ca90cab98e7c03f31a2.png) albo
albo ![\left[ \frac{0}{0} \right] \left[ \frac{0}{0} \right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/8e3f348a630785530b38a36fe9e9c071.png) .
.- Określamy symbol granicy i przekształcamy funkcję w następujący sposób:
Dalej pomocniczo obliczymy granicę
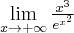 dwukrotnie stosując regułę de l'Hospitala:
Ostatecznie otrzymujemy
dwukrotnie stosując regułę de l'Hospitala:
Ostatecznie otrzymujemy
- Określamy symbol granicy: W tym przypadku, aby można było wykorzystać regułę de l'Hospitala, wystarczy sprowadzić ułamki do wspólnego mianownika. A zatem
- Stosujemy regułę de l'Hospitala po wykonaniu odpowiednich przekształceń:





![\dfrac{e^x-1}{2\sin x} = \left[\dfrac{0}{0}\right] \dfrac{e^x-1}{2\sin x} = \left[\dfrac{0}{0}\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/3a32e8a400e82e6025c8fc27f796d3e7.png)



![\underset{x\rightarrow +\infty }{\lim }\, \dfrac{x}{\ln x} = \left[\dfrac{\infty}{\infty}\right] \overset{\text{H}}{=} \underset{x\rightarrow +\infty }{\lim }\, \dfrac{x}{\ln x} = \left[\dfrac{\infty}{\infty}\right] \overset{\text{H}}{=}](https://port.edu.p.lodz.pl/filter/tex/pix.php/f51b93dc00924ac3be8ae55eb4aec36b.png)

![\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\ln x }{x} = \left[\dfrac{-\infty}{0^{+}}\right]. \underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\ln x }{x} = \left[\dfrac{-\infty}{0^{+}}\right].](https://port.edu.p.lodz.pl/filter/tex/pix.php/d8ff9a271b17743a4c7cfd0f3a66f70e.png)
![\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\ln x }{x} = \underset{x\rightarrow 0^{+} }{\lim }\, \ln x \cdot \dfrac{1}{x} =\left[-\infty \cdot \dfrac{1}{0^{+}}\right] = [-\infty \cdot \infty]=-\infty. \underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\ln x }{x} = \underset{x\rightarrow 0^{+} }{\lim }\, \ln x \cdot \dfrac{1}{x} =\left[-\infty \cdot \dfrac{1}{0^{+}}\right] = [-\infty \cdot \infty]=-\infty.](https://port.edu.p.lodz.pl/filter/tex/pix.php/d9c9c4343188476654c6443e78e3ba90.png)
![\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{(\ln x)'}{(x)'} =\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\frac{1}{x}}{1} = \left[\dfrac{1}{0^{+}}\right] = +\infty \underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{(\ln x)'}{(x)'} =\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\frac{1}{x}}{1} = \left[\dfrac{1}{0^{+}}\right] = +\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/307501b572f59af6a574a7f2021ad6b8.png)



![\underset{x\rightarrow 0}{\lim }\,\dfrac{x\cos 2x}{x+\arcsin x} = \left[\dfrac{0}{0}\right]\overset{\text{H}}{=} \underset{x\rightarrow 0}{\lim }\dfrac{(x\cos 2x)'}{(x+\arcsin x)'}=\underset{x\rightarrow 0}{\lim }\,\dfrac{\cos 2x-x\sin 2x\cdot 2}{1+\frac{1}{\sqrt{1-x^{2}}}}= \underset{x\rightarrow 0}{\lim }\,\dfrac{x\cos 2x}{x+\arcsin x} = \left[\dfrac{0}{0}\right]\overset{\text{H}}{=} \underset{x\rightarrow 0}{\lim }\dfrac{(x\cos 2x)'}{(x+\arcsin x)'}=\underset{x\rightarrow 0}{\lim }\,\dfrac{\cos 2x-x\sin 2x\cdot 2}{1+\frac{1}{\sqrt{1-x^{2}}}}=](https://port.edu.p.lodz.pl/filter/tex/pix.php/10b4959c1038fb647798ed685676c5a1.png)
![\left[\dfrac{1-0}{1+1}\right]=\dfrac{1}{2}\, \left[\dfrac{1-0}{1+1}\right]=\dfrac{1}{2}\,](https://port.edu.p.lodz.pl/filter/tex/pix.php/25eb870e22a13f078b899d09b5c337ee.png)
![\underset{x\rightarrow + \infty }{\lim }\dfrac{e^{x^{2}}}{x^{3}}=\left[ \dfrac{\infty }{\infty }\right] \overset{\text{H}}{=}\underset{x\rightarrow +\infty } {\lim }\dfrac{(e^{x^{2}})^{\prime }}{(x^{3})^{\prime }}=\underset{ x\rightarrow +\infty }{\lim }\dfrac{e^{x^{2}}\cdot 2x}{3x^{2}}=\underset{ x\rightarrow +\infty }{\lim }\dfrac{2e^{x^{2}}}{3x}=\left[ \dfrac{\infty }{\infty }\right] \overset{\text{H}}{=} \underset{x\rightarrow + \infty }{\lim }\dfrac{e^{x^{2}}}{x^{3}}=\left[ \dfrac{\infty }{\infty }\right] \overset{\text{H}}{=}\underset{x\rightarrow +\infty } {\lim }\dfrac{(e^{x^{2}})^{\prime }}{(x^{3})^{\prime }}=\underset{ x\rightarrow +\infty }{\lim }\dfrac{e^{x^{2}}\cdot 2x}{3x^{2}}=\underset{ x\rightarrow +\infty }{\lim }\dfrac{2e^{x^{2}}}{3x}=\left[ \dfrac{\infty }{\infty }\right] \overset{\text{H}}{=}](https://port.edu.p.lodz.pl/filter/tex/pix.php/5b80619ac8676c4a800681bf3a57b9d2.png)
![=\underset{ x\rightarrow +\infty }{\lim }\dfrac{(2e^{x^{2}})^{\prime }}{(3x)^{\prime }}=\underset{x\rightarrow +\infty }{\lim }\dfrac{2e^{x^{2}}\cdot 2x}{3 }=\left[ \dfrac{\infty}{3} \right] =\infty =\underset{ x\rightarrow +\infty }{\lim }\dfrac{(2e^{x^{2}})^{\prime }}{(3x)^{\prime }}=\underset{x\rightarrow +\infty }{\lim }\dfrac{2e^{x^{2}}\cdot 2x}{3 }=\left[ \dfrac{\infty}{3} \right] =\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/8a4a774eb1bb0f943edb6037da6c6f85.png)
![\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{\ln (\sin x )}{\ln ^{2}{x}}=\left[ \dfrac{-\infty }{\infty }\right] \overset{\text{H}}{=}\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{\frac{1}{\sin x}\cdot \cos x}{2\ln x \cdot \frac{1}{x}}=\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{x}{\sin x} \cdot \dfrac{\cos x}{2\ln x}=\left[ 1\cdot\dfrac{1}{-\infty}\right] =0 \underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{\ln (\sin x )}{\ln ^{2}{x}}=\left[ \dfrac{-\infty }{\infty }\right] \overset{\text{H}}{=}\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{\frac{1}{\sin x}\cdot \cos x}{2\ln x \cdot \frac{1}{x}}=\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{x}{\sin x} \cdot \dfrac{\cos x}{2\ln x}=\left[ 1\cdot\dfrac{1}{-\infty}\right] =0](https://port.edu.p.lodz.pl/filter/tex/pix.php/d561fe251231a59d20bc3ef61fef5c00.png)


![\underset{x\rightarrow +\infty }{\lim }\, \dfrac{x-\sin x }{x} = \left[\dfrac{\infty}{\infty}\right] \underset{x\rightarrow +\infty }{\lim }\, \dfrac{x-\sin x }{x} = \left[\dfrac{\infty}{\infty}\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/f48f480c622a09984ee03134a12800bd.png)

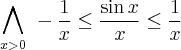
![\underset{x\rightarrow +\infty }{\lim }\dfrac{x-\sin x }{x}=\underset{x\rightarrow +\infty }{\lim }\left(1-\dfrac{\sin x}{x} \right)=[1-0]=1 \underset{x\rightarrow +\infty }{\lim }\dfrac{x-\sin x }{x}=\underset{x\rightarrow +\infty }{\lim }\left(1-\dfrac{\sin x}{x} \right)=[1-0]=1](https://port.edu.p.lodz.pl/filter/tex/pix.php/4c5f265f4283e60e82ecd5cf8dc4ff7a.png)
![\underset{x\rightarrow +\infty}{\lim }\,\dfrac{\sqrt{x^2+1}}{x}=\left[\dfrac{\infty}{\infty}\right]\overset{\text{H}}{=}\underset{x\rightarrow +\infty}{\lim }\,\dfrac{\frac{1}{2\sqrt{x^2+1}}\cdot 2x}{1}=\underset{x\rightarrow +\infty}{\lim }\,\dfrac{x}{\sqrt{x^2+1}}\overset{\text{H}}{=}\underset{x\rightarrow+ \infty}{\lim }\,\dfrac{\sqrt{x^2+1}}{x} \underset{x\rightarrow +\infty}{\lim }\,\dfrac{\sqrt{x^2+1}}{x}=\left[\dfrac{\infty}{\infty}\right]\overset{\text{H}}{=}\underset{x\rightarrow +\infty}{\lim }\,\dfrac{\frac{1}{2\sqrt{x^2+1}}\cdot 2x}{1}=\underset{x\rightarrow +\infty}{\lim }\,\dfrac{x}{\sqrt{x^2+1}}\overset{\text{H}}{=}\underset{x\rightarrow+ \infty}{\lim }\,\dfrac{\sqrt{x^2+1}}{x}](https://port.edu.p.lodz.pl/filter/tex/pix.php/4eae5571d7aa2578a16e83b947c34088.png)




![\lim\limits_{x\to + \infty }\,x^2 \,e^{-x}= \left[ \infty\cdot0 \,\right] \lim\limits_{x\to + \infty }\,x^2 \,e^{-x}= \left[ \infty\cdot0 \,\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/0516aaa46e442443d1fec0c616104686.png)
![\lim\limits_{x\to +\infty }\,x^2 \,e^{-x}=\lim\limits_{x\to +\infty } \dfrac{x^2}{e^x}=\left[ \dfrac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to +\infty } \dfrac{(x^2)'}{(e^x)'} = \lim\limits_{x\to +\infty }\,\dfrac{2x}{e^x} \lim\limits_{x\to +\infty }\,x^2 \,e^{-x}=\lim\limits_{x\to +\infty } \dfrac{x^2}{e^x}=\left[ \dfrac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to +\infty } \dfrac{(x^2)'}{(e^x)'} = \lim\limits_{x\to +\infty }\,\dfrac{2x}{e^x}](https://port.edu.p.lodz.pl/filter/tex/pix.php/7a87707e4486a2e482602f1fd1c8330e.png)
![=\left[ \dfrac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to +\infty }\,\dfrac{(2x)'}{(e^x)'} = \lim\limits_{x\to +\infty }\,\dfrac{2}{e^x} = \left[ \dfrac{2}{\infty} \right] = 0 =\left[ \dfrac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to +\infty }\,\dfrac{(2x)'}{(e^x)'} = \lim\limits_{x\to +\infty }\,\dfrac{2}{e^x} = \left[ \dfrac{2}{\infty} \right] = 0](https://port.edu.p.lodz.pl/filter/tex/pix.php/8568adb4c17df80de0f81c62d130d8ea.png)
![\lim\limits_{x\to 0^{+}}\,x \ln x=\left[ 0\cdot (-\infty) \right] \lim\limits_{x\to 0^{+}}\,x \ln x=\left[ 0\cdot (-\infty) \right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/135067031e61492d7de5429a2b9c1ee6.png)
![\lim\limits_{x\to 0^{+}} x\ln x=\lim\limits_{x\to 0^+}\dfrac{\ln x}{\frac{1}{x}}=\left[ \dfrac{-\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to 0^+}\dfrac{(\ln x)'}{(\frac{1}{x})'} \lim\limits_{x\to 0^{+}} x\ln x=\lim\limits_{x\to 0^+}\dfrac{\ln x}{\frac{1}{x}}=\left[ \dfrac{-\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to 0^+}\dfrac{(\ln x)'}{(\frac{1}{x})'}](https://port.edu.p.lodz.pl/filter/tex/pix.php/7aa38f9e30534a256c15a186be3e5035.png)


![\lim\limits_{x\to 0^{+} }x^x=\left[ 0^0\right] \lim\limits_{x\to 0^{+} }x^x=\left[ 0^0\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/abd653623333c1342282ffac79945643.png)

![\displaystyle \lim\limits_{x\to 0^{+} }x^x=\lim\limits_{x\to 0^{+} }e^{x\ln x}=\left[ e^0 \right]=1 \displaystyle \lim\limits_{x\to 0^{+} }x^x=\lim\limits_{x\to 0^{+} }e^{x\ln x}=\left[ e^0 \right]=1](https://port.edu.p.lodz.pl/filter/tex/pix.php/e0bdf2feebca2cc6a672b588f7b79179.png)


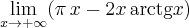
![\lim\limits_{x\to+ \infty } (e^{x^2}-x^3)=\left[\infty-\infty\right] =\lim\limits_{x\to +\infty } e^{x^2}\left(1-\dfrac{x^3}{e^{x^2}}\right) \lim\limits_{x\to+ \infty } (e^{x^2}-x^3)=\left[\infty-\infty\right] =\lim\limits_{x\to +\infty } e^{x^2}\left(1-\dfrac{x^3}{e^{x^2}}\right)](https://port.edu.p.lodz.pl/filter/tex/pix.php/2edce056c38c4224c25761738706ec2b.png)
![\lim\limits_{x\to+ \infty }\dfrac{x^3}{e^{x^2}}=\left[ \dfrac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to+ \infty } \dfrac{(x^3)'}{(e^{x^2})'} = \lim\limits_{x\to +\infty }\,\dfrac{3x^2}{2x\,e^{x^2}} = \lim\limits_{x\to +\infty }\,\dfrac{3x}{2\,e^{x^2}} \lim\limits_{x\to+ \infty }\dfrac{x^3}{e^{x^2}}=\left[ \dfrac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to+ \infty } \dfrac{(x^3)'}{(e^{x^2})'} = \lim\limits_{x\to +\infty }\,\dfrac{3x^2}{2x\,e^{x^2}} = \lim\limits_{x\to +\infty }\,\dfrac{3x}{2\,e^{x^2}}](https://port.edu.p.lodz.pl/filter/tex/pix.php/92411a055f061f6f408303086c95e284.png)
![= \left[ \dfrac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to +\infty }\,\dfrac{(3x)'}{(2e^{x^2})'} = \lim\limits_{x\to+ \infty }\,\dfrac{3}{4x\,e^{x^2}} = \left[ \dfrac{3}{\infty} \right] = 0 = \left[ \dfrac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\to +\infty }\,\dfrac{(3x)'}{(2e^{x^2})'} = \lim\limits_{x\to+ \infty }\,\dfrac{3}{4x\,e^{x^2}} = \left[ \dfrac{3}{\infty} \right] = 0](https://port.edu.p.lodz.pl/filter/tex/pix.php/6d510f636f7469e87cfe2c0a7be30fe0.png)
![\lim\limits_{x\to+ \infty } e^{x^2}(1-\frac{x^3}{e^{x^2}})=\left[ \infty \cdot(1-0) \right]=\infty \lim\limits_{x\to+ \infty } e^{x^2}(1-\frac{x^3}{e^{x^2}})=\left[ \infty \cdot(1-0) \right]=\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/0d95713a31528a1b492e9b704cf372dd.png)
![\lim\limits_{x\to 0^{+} }\left( \dfrac1x-\dfrac{1}{\sin x}\right) = \left[\infty-\infty\right] \lim\limits_{x\to 0^{+} }\left( \dfrac1x-\dfrac{1}{\sin x}\right) = \left[\infty-\infty\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/5f26034f064d8d5c466b7ed92700d9d8.png)
![\lim\limits_{x\to 0^{+} }\left( \dfrac1x-\dfrac{1}{\sin x}\right) = \lim\limits_{x\to 0^{+} }\dfrac{\sin x-x}{x\sin x}= \left[ \dfrac{0}{0} \right] \overset{\text{H}}{=} \lim\limits_{x\to 0^{+} }\dfrac{(\sin x-x)'}{(x\sin x)'} \lim\limits_{x\to 0^{+} }\left( \dfrac1x-\dfrac{1}{\sin x}\right) = \lim\limits_{x\to 0^{+} }\dfrac{\sin x-x}{x\sin x}= \left[ \dfrac{0}{0} \right] \overset{\text{H}}{=} \lim\limits_{x\to 0^{+} }\dfrac{(\sin x-x)'}{(x\sin x)'}](https://port.edu.p.lodz.pl/filter/tex/pix.php/1f40b9f8f00d5187cf676e7f63e0466b.png)
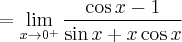
![= \left[ \dfrac{0}{0} \right]\overset{\text{H}}{=} \lim\limits_{x\to 0^{+} }\dfrac{-\sin x}{\cos x+\cos x-x\sin x}= \left[ \dfrac{0}{2} \right]=0 = \left[ \dfrac{0}{0} \right]\overset{\text{H}}{=} \lim\limits_{x\to 0^{+} }\dfrac{-\sin x}{\cos x+\cos x-x\sin x}= \left[ \dfrac{0}{2} \right]=0](https://port.edu.p.lodz.pl/filter/tex/pix.php/c3cb9ea4224a3a4222c2267240aaffab.png)
![\lim\limits_{x\to +\infty }(\pi\, x-2x\,\text{arctg} x)=\left[\infty-\infty\right] = \lim\limits_{x\to +\infty }x\,(\pi\,-2\,\text{arctg} x)=\left[ \infty\cdot 0\right] \lim\limits_{x\to +\infty }(\pi\, x-2x\,\text{arctg} x)=\left[\infty-\infty\right] = \lim\limits_{x\to +\infty }x\,(\pi\,-2\,\text{arctg} x)=\left[ \infty\cdot 0\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/f8c06a25e94b80f9e4e415d8f906a8a4.png)
![= \lim\limits_{x\to+ \infty }\dfrac{\pi\,-2\,\text{arctg} x}{\frac1x}= \left[ \dfrac{0}{0} \right] \overset{\text{H}}{=} \lim\limits_{x\to+\infty }\dfrac{(\pi\,-2\,\text{arctg} x)'}{(\frac1x)'} = \lim\limits_{x\to+ \infty }\dfrac{\pi\,-2\,\text{arctg} x}{\frac1x}= \left[ \dfrac{0}{0} \right] \overset{\text{H}}{=} \lim\limits_{x\to+\infty }\dfrac{(\pi\,-2\,\text{arctg} x)'}{(\frac1x)'}](https://port.edu.p.lodz.pl/filter/tex/pix.php/7dcb0b4aba4c455a35f6e03efb894949.png)
