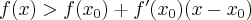5.1 Badanie wklęsłości i wypukłości funkcji
Teoria
Definicja
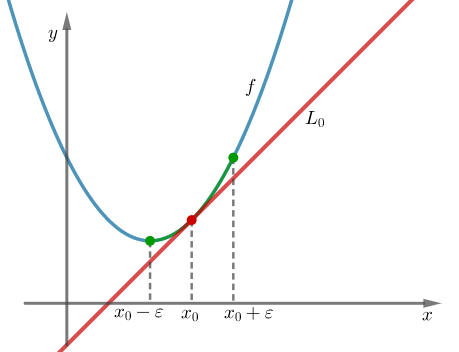
Załóżmy, że funkcja  jest różniczkowalna na pewnym otoczeniu punktu
jest różniczkowalna na pewnym otoczeniu punktu  . Niech
. Niech 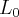 będzie styczną do jej wykresu w punkcie
będzie styczną do jej wykresu w punkcie 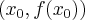 . Funkcję
. Funkcję  nazywamy wypukłą w punkcie
nazywamy wypukłą w punkcie  , jeżeli istnieje takie sąsiedztwo
, jeżeli istnieje takie sąsiedztwo  punktu
punktu  , że dla każdego
, że dla każdego  punkty tej krzywej leżą powyżej stycznej
punkty tej krzywej leżą powyżej stycznej 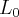 , tzn. istnieje sąsiedztwo
, tzn. istnieje sąsiedztwo  punktu
punktu  takie, że dla
takie, że dla  zachodzi nierówność
zachodzi nierówność
Definicja
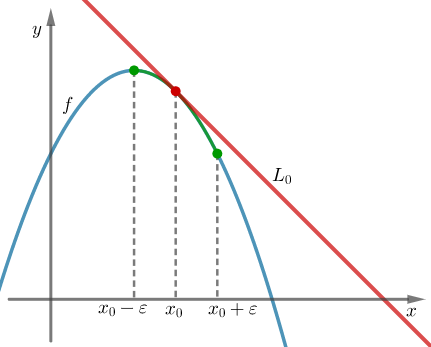
Załóżmy, że funkcja  jest różniczkowalna na pewnym otoczniu punktu
jest różniczkowalna na pewnym otoczniu punktu  . Niech
. Niech 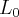 będzie styczną do jej wykresu w punkcie
będzie styczną do jej wykresu w punkcie 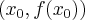 . Funkcję
. Funkcję  nazywamy wklęsłą w punkcie
nazywamy wklęsłą w punkcie  , jeżeli istnieje takie sąsiedztwo
, jeżeli istnieje takie sąsiedztwo  punktu
punktu  , że dla każdego
, że dla każdego  punkty tej krzywej leżą poniżej stycznej
punkty tej krzywej leżą poniżej stycznej 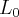 , tzn. istnieje sąsiedztwo
, tzn. istnieje sąsiedztwo  punktu
punktu  takie, że dla
takie, że dla  zachodzi nierówność
zachodzi nierówność
Definicja
Mówimy, że funkcja 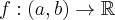 jest wypukła (wklęsła) na przedziale
jest wypukła (wklęsła) na przedziale  , gdy jest wypukła (wklęsła) w każdym punkcie tego przedziału.
, gdy jest wypukła (wklęsła) w każdym punkcie tego przedziału.
Twierdzenie -- warunek wystarczający wypukłości krzywej
Jeżeli funkcja  jest dwukrotnie różniczkowalna na przedziale
jest dwukrotnie różniczkowalna na przedziale  oraz
oraz  dla każdego
dla każdego  , to funkcja
, to funkcja  jest wypukła na tym przedziale.
jest wypukła na tym przedziale.
Twierdzenie -- warunek wystarczający wklęsłości krzywej
Jeżeli funkcja  jest dwukrotnie różniczkowalna na przedziale
jest dwukrotnie różniczkowalna na przedziale  oraz
oraz  dla każdego
dla każdego  , to funkcja
, to funkcja  jest wklęsła na tym przedziale.
jest wklęsła na tym przedziale.