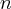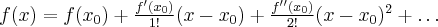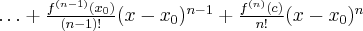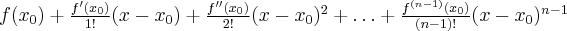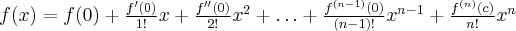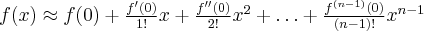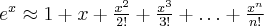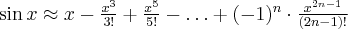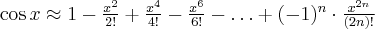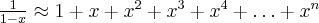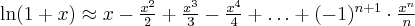Rachunek różniczkowy funkcji jednej zmiennej

Powyższy wzór nazywany jest wzorem Taylora, zaś wyrażenie 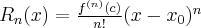$R_n(x)=\frac{f^{(n)}(c)}{n!}(x-x_0)^{n}$ resztą Taylora w postaci Lagrange'a. Wielomian postaci

$f(x_0) + \frac{f'(x_0)}{1!}(x-x_0) + \frac{f''(x_0)}{2!}(x-x_0)^2 + \ldots + \frac{f^{(n-1)}(x_0)}{(n-1)!}(x-x_0)^{n-1}$

nazywamy wielomianem Taylora stopnia $n-1$ w punkcie $x_0$.

Jeżeli $x_0=0$, to wzór Taylora ma postać

$f(x)=f(0)+\frac{f^\prime(0)}{1!}x+\frac{f^{\prime\prime}( 0)}{2!}x^2+ \ldots +\frac{f^{(n-1)}(0)}{(n-1)!}x^{n-1}+\frac{f^{(n)}(c)}{n!}x^{n}$

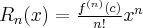i nazywany jest wzorem Maclaurina (punkt $c$ leży pomiędzy $0$ i $x$). Pomijając w powyższym wzorze resztę Taylora $R_n(x)=\frac{f^{(n)}(c)}{n!}x^{n}$, otrzymujemy przybliżenie (aproksymację) funkcji $f$ za pomocą wielomianu Maclaurina:

$f(x)\approx f(0)+\frac{f'(0)}{1!}x+\frac{f''( 0)}{2!}x^2+ \ldots +\frac{f^{(n-1)}(0)}{(n-1)!}x^{n-1}$,

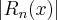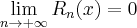przy czym błąd bezwzględny tego przybliżenia wynosi $|R_n(x)|$. Jeżeli wszystkie pochodne funkcji $f$ są wspólnie ograniczone, to $\lim\limits_{n\to +\infty}R_n(x)=0$. Wówczas możemy obliczyć wartość funkcji $f$ z dowolną dokładnością.

Przybliżenie wybranych funkcji za pomocą wzoru Maclaurina:

$e^x\approx 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\ldots +\frac{x^{n}}{n!}$,

$\sin x\approx x-\frac{x^3}{3!}+\frac{x^5}{5!}-\ldots +(-1)^n\cdot\frac{x^{2n-1}}{(2n-1)!}$,

$\cos x\approx 1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}-\ldots +(-1)^n\cdot\frac{x^{2n}}{(2n)!}$,

$\frac{1}{1-x}\approx 1+x+x^2+x^3+x^4+\ldots +x^n$,

$\ln (1+x)\approx x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\ldots + (-1)^{n+1}\cdot \frac{x^n}{n}$.