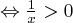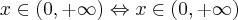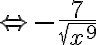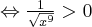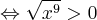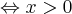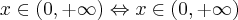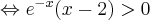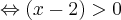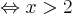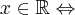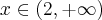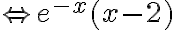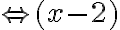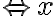Rachunek różniczkowy funkcji jednej zmiennej

Przykład 1

Wykażemy, że funkcja $f(x)=x\ln x$ jest wypukła w całej dziedzinie.

Rozwiązanie

Dziedziną badanej funkcji jest zbiór $D=(0,+\infty )$.

Obliczamy pochodną tej funkcji 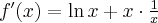$f^{\prime }(x)=\ln x+x\cdot\frac{1}{x}$. Zatem $f^{\prime }(x)=\ln x+1$, $x\in (0,+\infty )$.

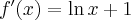Obliczamy teraz pochodną drugiego rzędu 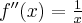$f^{\prime \prime }(x)= \frac{1}{x}$, $x\in (0,+\infty)$.

Rozwiązujemy nierówność:

$f^{\prime \prime }(x)>0$ $\Leftrightarrow \frac{1}{x}>0$ i $x\in (0,+\infty )\Leftrightarrow x\in (0,+\infty)$.

Ponieważ 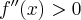$f^{\prime \prime}(x)>0$ dla każdego $x\in (0,+\infty )$, to wnioskujemy, że funkcja $f(x)=x\ln x$ jest wypukła w każdym punkcie swojej dziedziny.

Przykład 2

Wykażemy, że funkcja $f(x)=-\frac{4}{5\sqrt{x^{5}}}$ jest wklęsła w całej dziedzinie.

Rozwiązanie

Dziedziną badanej funkcji jest zbiór $D = (0,+\infty)$.

Obliczamy pochodną tej funkcji 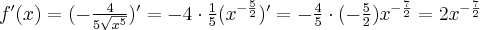$f^{\prime }(x)=(-\frac{4}{5\sqrt{x^{5}} })^{\prime }=-4\cdot \frac{1}{5}(x^{-\frac{5}{2}})^{\prime }=-\frac{4}{5} \cdot (-\frac{5}{2})x^{-\frac{7}{2}}=2x^{-\frac{7}{2}}$, czyli $f^{\prime}(x)=\frac{2}{\sqrt{x^{7}}}$, $x\in (0,+\infty )$.

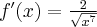Obliczamy teraz pochodną drugiego rzędu tej funkcji 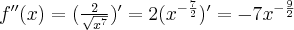$f^{\prime \prime }(x)=(\frac{2}{\sqrt{x^{7}}})^{\prime }=2(x^{-\frac{7}{2}})^{\prime }=-7x^{-\frac{9}{2}}$. Zatem $f^{\prime \prime }(x)=-\frac{7}{\sqrt{x^{9}}}$, $x\in (0,+\infty)$.

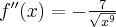Rozwiązujemy nierówność:

$f^{\prime \prime }(x)$ $\Leftrightarrow -\frac{7}{\sqrt{x^{9}}}$ $\Leftrightarrow \frac{1}{\sqrt{x^{9}}}>0$ $\Leftrightarrow \sqrt{x^{9}}>0$ $\Leftrightarrow x>0$ i $x\in (0,+\infty )\Leftrightarrow x\in (0,+\infty )$.

Ponieważ $f^{\prime \prime }(x)$ dla każdego $x\in (0,+\infty )$, zatem funkcja $f(x)=-\frac{4}{5\sqrt{x^{5}}}$ jest wklęsła w każdym punkcie swojej dziedziny.

Przykład 3

Wyznaczymy przedziały wypukłości/wklęsłości funkcji $f(x)=xe^{-x}$.

Rozwiązanie

Dziedziną badanej funkcji jest zbiór $x\in \mathbb{R}$.

Obliczamy pochodną tej funkcji 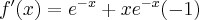$f^{\prime }(x)=e^{-x}+xe^{-x}(-1)$, czyli $f^{\prime }(x)=e^{-x}(1-x)$, $x\in \mathbb{R}$.

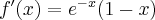Obliczamy teraz pochodną drugiego rzędu 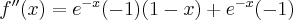$\ f^{\prime \prime }(x)=e^{-x}(-1)(1-x)+e^{-x}(-1)$. Zatem $f^{\prime \prime }(x)=e^{-x}(x-2)$, $x\in \mathbb{R}$.

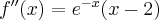Rozwiązujemy nierówności:

$f^{\prime \prime }(x)>0$ $\Leftrightarrow e^{-x}(x-2)>0$ $\Leftrightarrow (x-2)>0$ $\Leftrightarrow x>2$ i $x\in \mathbb{R}\Leftrightarrow$ $x\in (2,+\infty )$,

$f^{\prime \prime }(x)$ $\Leftrightarrow e^{-x}(x-2)$ $\Leftrightarrow (x-2)$ $\Leftrightarrow x$ i $x\in \mathbb{R}\Leftrightarrow$ $x\in (-\infty ,2)$.

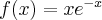Ponieważ $f^{\prime \prime }(x)>0$ dla każdego $x\in (2,+\infty)$ zatem funkcja $f(x)=xe^{-x}$ jest wypukła na przedziale $(2,+\infty)$.

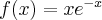Ponieważ $f^{\prime \prime }(x)$ dla każdego $x\in (-\infty ,2)$ zatem funkcja $f(x)=xe^{-x}$ jest wklęsła na przedziale $(-\infty ,2)$.