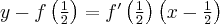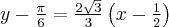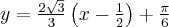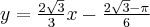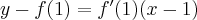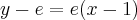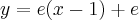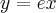1.3 Interpretacja geometryczna pochodnej w punkcie
Przykłady
Przykład 1
Wyznaczymy równanie stycznej do wykresu funkcji 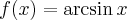 w punkcie
w punkcie 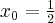 .
.
Rozwiązanie
Równanie stycznej do wykresu funkcji wyznaczymy korzystając ze wzoru:
Pochodna funkcji 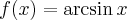 jest równa
jest równa 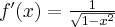 ,
, 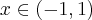 .
.
Obliczamy teraz wartości: funkcji i pochodnej funkcji w punkcie  Mamy
Mamy 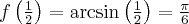 ,
, 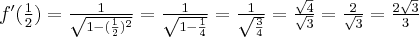 .
.
Podstawiamy obliczone wartości do równania stycznej i otrzymujemy:
Zatem styczna ma równanie
Przykład 2
Wyznaczymy równanie stycznej do wykresu funkcji 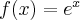 w punkcie
w punkcie  .
.
Rozwiązanie
Równanie stycznej do wykresu funkcji wyznaczymy korzystając ze wzoru:
Pochodna funkcji 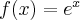 jest równa
jest równa 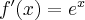 ,
,  .
.
Obliczamy teraz wartości: funkcji i pochodnej funkcji w punkcie  . Otrzymujemy
. Otrzymujemy 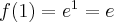 ,
, 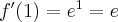 .
.
Podstawiamy obliczone wartości do równania stycznej. Otrzymujemy:
Zatem styczna ma równanie