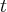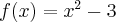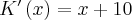7. Pochodna w zastosowaniach praktycznych - przykłady
Od podwojonej pewnej liczby ujemnej odjęto kwadrat jej odwrotności. Jaka powinna być ta liczba, aby wartość tak otrzymanego wyrażenia była największa?
Oznaczmy przez  szukaną liczbę. Wówczas funkcja opisująca warunki zadania ma postać:
szukaną liczbę. Wówczas funkcja opisująca warunki zadania ma postać:
Wyznaczamy punkty stacjonarne funkcji  :
:
Rozwiązujemy odpowiednie nierówności pamiętając, że  :
:
Z I warunku wystarczającego istnienia ekstremum lokalnego wynika, że funkcja  ma maksimum lokalne dla
ma maksimum lokalne dla  . Czyli szukaną liczbą jest
. Czyli szukaną liczbą jest  .
.
Pewien tokarz otrzymał mosiężną kulę o promieniu  by wykonać z niej walec o jak największej objętości. Jakie będą wymiary tego walca i jaka będzie objętość skrawków?
by wykonać z niej walec o jak największej objętości. Jakie będą wymiary tego walca i jaka będzie objętość skrawków?
Niech  oznacza promień podstawy walca wpisanego w kulę, zaś
oznacza promień podstawy walca wpisanego w kulę, zaś  jego wysokość. Wykonujemy pomocniczy rysunek (aplet), na którym możemy zaobserwować, w jaki sposób objętość walca zależy od jego wysokości:
jego wysokość. Wykonujemy pomocniczy rysunek (aplet), na którym możemy zaobserwować, w jaki sposób objętość walca zależy od jego wysokości:
Przypomnijmy wzór na objętość walca
Z twierdzenia Pitagorasa (zastosowanego do trójkąta prostokątnego będącego połową przekroju osiowego walca) wynika, że
Stąd  . Wstawiając do wzoru na objętość walca otrzymujemy:
. Wstawiając do wzoru na objętość walca otrzymujemy:
Dalej wyznaczymy największą wartość funkcji  . W tym celu obliczamy pochodną
. W tym celu obliczamy pochodną
i przyrównujemy ją do zera:
 dla
dla  , natomiast
, natomiast  dla
dla  . A zatem walec przyjmuje największą objętość dla
. A zatem walec przyjmuje największą objętość dla  cm i objętość ta jest równa
cm i objętość ta jest równa
Pozostaje obliczyć jeszcze objętość kuli
i na koniec objętość skrawków
Dana jest funkcja ![f(x)=\frac12(x+3)\sqrt{2-x},\;\; x\in [-2,2] f(x)=\frac12(x+3)\sqrt{2-x},\;\; x\in [-2,2]](https://port.edu.p.lodz.pl/filter/tex/pix.php/b08973d0afd694288627df52f04ec353.png) . Wyznacz taki punkt na wykresie funkcji
. Wyznacz taki punkt na wykresie funkcji  , którego odległość od punktu
, którego odległość od punktu  jest najmniejsza.
jest najmniejsza.
Niech ![P=(x,f(x)), \;x\in [-2,2] P=(x,f(x)), \;x\in [-2,2]](https://port.edu.p.lodz.pl/filter/tex/pix.php/229ff2b9b24066c4212d1f1f5204f0d5.png) będzie punktem wykresu funkcji
będzie punktem wykresu funkcji  . Wówczas odległość
. Wówczas odległość  tego punktu od początku układu współrzędnych można przedstawić jako funkcję zmiennej
tego punktu od początku układu współrzędnych można przedstawić jako funkcję zmiennej 
Po podstawieniu otrzymujemy
Obliczamy najpierw pochodną funkcji 
i przyrównujemy ją do zera:
Zgodnie z algorytmem wyznaczania ekstremów globalnych funkcja  może posiadać minimum globalne w punktach:
może posiadać minimum globalne w punktach:  oraz
oraz  . Obliczamy wartości funkcji we wskazanych punktach:
. Obliczamy wartości funkcji we wskazanych punktach:
Stąd wynika, że funkcja  przyjmuje wartość najmniejszą na przedziale
przyjmuje wartość najmniejszą na przedziale ![[-2,2] [-2,2]](https://port.edu.p.lodz.pl/filter/tex/pix.php/98fab4cc523eb62bb9cf3a4fbefb7a69.png) w punktach
w punktach  oraz
oraz  . Punkty wykresu funkcji
. Punkty wykresu funkcji  , których odległość od początku układu jest najmniejsza to
, których odległość od początku układu jest najmniejsza to  oraz
oraz  . Odległość ta wynosi
. Odległość ta wynosi  .
.
Poniższy aplet przedstawia wykres funkcji  z ruchomym punktem
z ruchomym punktem 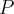 oraz funkcję
oraz funkcję  .
.
Dwa miasta  i
i  położone po przeciwnych stronach rzeki trzeba połączyć drogą z mostem prostopadłym do brzegów rzeki o prostoliniowych i równoległych brzegach. W którym miejscu należy wybudować most, aby droga łącząca te miasta miała najmniejszą długość? Odległość miasta
położone po przeciwnych stronach rzeki trzeba połączyć drogą z mostem prostopadłym do brzegów rzeki o prostoliniowych i równoległych brzegach. W którym miejscu należy wybudować most, aby droga łącząca te miasta miała najmniejszą długość? Odległość miasta  od rzeki wynosi
od rzeki wynosi  km, odległość miasta
km, odległość miasta  od rzeki wynosi
od rzeki wynosi  km, zaś odległość między rzutami miast na linię rzeki to
km, zaś odległość między rzutami miast na linię rzeki to  km.
km.

Niech  będzie odległością mostu od rzutu miasta
będzie odległością mostu od rzutu miasta  na linię rzeki. Wówczas
na linię rzeki. Wówczas  , zaś droga łącząca miasta
, zaś droga łącząca miasta  i
i  ma długość
ma długość
Ponieważ odcinek  równy długości mostu ma stałą długość, wystarczy, że znajdziemy najmniejszą wartość funkcji
równy długości mostu ma stałą długość, wystarczy, że znajdziemy najmniejszą wartość funkcji  na przedziale
na przedziale ![[0,21] [0,21]](https://port.edu.p.lodz.pl/filter/tex/pix.php/faa027f55788c0be58d3fa3d24c10ae1.png) .
.
i przyrównujemy ją do zera:
Ponieważ
więc
Zgodnie z algorytmem wyznaczania ekstremów globalnych funkcja  może posiadać minimum globalne w punktach:
może posiadać minimum globalne w punktach:  oraz
oraz  . Obliczamy wartości funkcji we wskazanych punktach:
. Obliczamy wartości funkcji we wskazanych punktach:
Stąd wynika, że funkcja  przyjmuje wartość najmniejszą na przedziale
przyjmuje wartość najmniejszą na przedziale ![[0,21] [0,21]](https://port.edu.p.lodz.pl/filter/tex/pix.php/faa027f55788c0be58d3fa3d24c10ae1.png) w punkcie
w punkcie 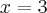 . Most należy zatem wybudować w odległości
. Most należy zatem wybudować w odległości  km od miasta
km od miasta  (licząc wzdłuż brzegu rzeki).
(licząc wzdłuż brzegu rzeki).
Stacja orbitalna porusza się prostoliniowo na wysokości  km nad Ziemią z prędkością
km nad Ziemią z prędkością  km/h. Antena odbierająca sygnały znajduje się bezpośrednio pod trajektorią stacji. W każdej chwili oś anteny jest skierowana na stację. Jaka jest prędkość kątowa anteny w chwili, gdy stacja znajduje się w odległości
km/h. Antena odbierająca sygnały znajduje się bezpośrednio pod trajektorią stacji. W każdej chwili oś anteny jest skierowana na stację. Jaka jest prędkość kątowa anteny w chwili, gdy stacja znajduje się w odległości  km od anteny?
km od anteny?
Stół bilardowy ma następujący kształt (bandy są w kształcie parabol). Gracz ma możliwość ustawienia bili w dowolnym miejscu na linii łączącej wierzchołki parabol. Jego zadanie polega na trafieniu do pokazanego otworu przy wykorzystaniu dokładnie jednego odbicia od bandy. Zakładając, że ustawił bilę w konkretnym miejscu, w którym kierunku powinien uderzyć?
Obróćmy stół bilardowy i opiszmy go funkcjami następująco:

Rozważymy jedną przykładową sytuację. Czytelnik może przeanalizować każdy inny przypadek samodzielnie. Załóżmy zatem, że otwór na stole bilardowym znajduje się w miejscu:  Z prawa odbicia wynika, że bila (która leży na części osi
Z prawa odbicia wynika, że bila (która leży na części osi  zawartej pomiędzy parabolami) pchnięta w stronę ramienia paraboli, odbije się od niej pod kątem równym kątowi padania na to ramię, czyli
zawartej pomiędzy parabolami) pchnięta w stronę ramienia paraboli, odbije się od niej pod kątem równym kątowi padania na to ramię, czyli

będzie poruszała się wzdłuż prostej padania i po odbiciu wróci wzdłuż prostej odbicia.
Prosta  jest styczną do paraboli w punkcie, w którym uderzy bila, prosta
jest styczną do paraboli w punkcie, w którym uderzy bila, prosta 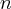 jest prostopadła do stycznej, kąty padania i odbicia pokazane są na rysunku.
jest prostopadła do stycznej, kąty padania i odbicia pokazane są na rysunku.
Zakładamy, że bilę umieścimy na stole bilardowym w punkcie 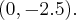
Wówczas należy uderzyć bilę w kierunku prostej o równaniu 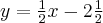 w kierunku lewej bandy (w przypadku uderzania w prawą bandę, prosta miałaby równanie
w kierunku lewej bandy (w przypadku uderzania w prawą bandę, prosta miałaby równanie 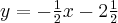 ).
).
Bila odbije się od bandy w punkcie 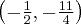 .
.
Styczna do bandy w tym punkcie ma równanie 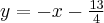 , zaś prosta odbicia
, zaś prosta odbicia 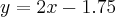 .
.
Bila, po odbicu, potoczy się do wskazanego otworu.
Koszt całkowity produkcji zależny od wielkości produkcji określa funkcja: 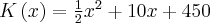 .
.
(a) Wyznaczymy koszt krańcowy dla pewnych wielkości produkcji.
(b) Sprawdzimy, kiedy producent zrealizuje maksymalny zysk (optimum ekonomiczne) przy określonej cenie sprzedaży jednostki produktu.
(c) Ustalimy wielkość produkcji zapewniającą minimalny koszt jednostkowy (optimum techniczne).
(a) Koszt krańcowy produkcji jest równy pochodnej funkcji  :
:
Dla wielkości produkcji 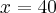 ,
, 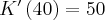 , zaś dla
, zaś dla 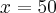 ,
, 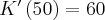 . Oznacza to, że wytworzenie dodatkowej jednostki produktu przy wielkości produkcji
. Oznacza to, że wytworzenie dodatkowej jednostki produktu przy wielkości produkcji 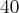 jednostek wynosi
jednostek wynosi 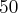 jednostek pieniężnych, a przy wielkości produkcji
jednostek pieniężnych, a przy wielkości produkcji 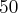 jednostek wynosi więcej, bo
jednostek wynosi więcej, bo 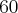 jednostek pieniężnych.
jednostek pieniężnych.
(b) Zakładamy, że cała produkcja może zostać sprzedana. Załóżmy teraz , że cena sprzedaży jednostki produktu wynosi 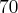 j.p. Niech funkcja
j.p. Niech funkcja 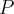 oznacza przychód ze sprzedaży,
oznacza przychód ze sprzedaży, 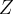 - zysk producenta. Wtedy:
- zysk producenta. Wtedy: 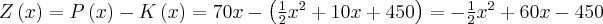 .
. 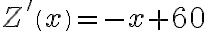 ,
, 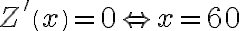 . Ponadto
. Ponadto 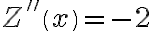 . Oznacza to, że przy wielkości produkcji
. Oznacza to, że przy wielkości produkcji 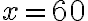 jednostek producent osiągnie maksymalny zysk w wysokości
jednostek producent osiągnie maksymalny zysk w wysokości 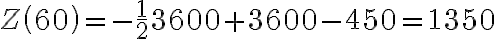 , czyli
, czyli 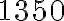 j.p. (c) Niech funkcja
j.p. (c) Niech funkcja 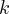 oznacza koszt jednostkowy.
oznacza koszt jednostkowy. 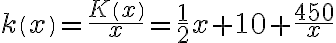 .
. 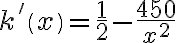 . Stąd
. Stąd 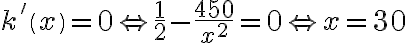 . Ponadto
. Ponadto 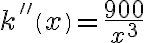 i
i 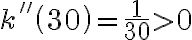 . Tym samym przy produkcji
. Tym samym przy produkcji 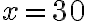 j.p. koszt jednostkowy jest minimalny i wynosi
j.p. koszt jednostkowy jest minimalny i wynosi 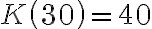 j.p.
j.p.

















![d(x)=\sqrt{x^2+\tfrac14(x+3)^2(2-x)}=\frac12\sqrt{-x^3+3x+18}, \, x\in [-2,2] d(x)=\sqrt{x^2+\tfrac14(x+3)^2(2-x)}=\frac12\sqrt{-x^3+3x+18}, \, x\in [-2,2]](https://port.edu.p.lodz.pl/filter/tex/pix.php/0961fa07615b6f4fe26e2e047be82b00.png)








![x\in [0,21] x\in [0,21]](https://port.edu.p.lodz.pl/filter/tex/pix.php/a837523de1167fc1a1b5fee332fe474c.png)
![f^\prime (x)=0 \Leftrightarrow \frac{x}{\sqrt{x^{2}+4}}=\frac{21-x}{\sqrt{(21-x)^{2}+144}} \Leftrightarrow \left(\frac{x^2}{x^{2}+4}=\frac{(21-x)^2}{(21-x)^{2}+144} \wedge x\in [0,21]\right). f^\prime (x)=0 \Leftrightarrow \frac{x}{\sqrt{x^{2}+4}}=\frac{21-x}{\sqrt{(21-x)^{2}+144}} \Leftrightarrow \left(\frac{x^2}{x^{2}+4}=\frac{(21-x)^2}{(21-x)^{2}+144} \wedge x\in [0,21]\right).](https://port.edu.p.lodz.pl/filter/tex/pix.php/8c398f262d63e7d9e375ace25222b1bd.png)