6. Badanie przebiegu zmienności funkcji
Teoria
Badanie przebiegu zmienności funkcji  jest zadaniem złożonym i obejmuje kilka etapów:
jest zadaniem złożonym i obejmuje kilka etapów:
- wyznaczenie dziedziny funkcji,
- wyznaczenie asymptot wykresu funkcji,
- wyznaczenie przedziałów monotoniczności i ekstremów lokalnych funkcji (badanie pierwszej pochodnej funkcji: rozwiązanie równania
 oraz nierówności
oraz nierówności  i
i  ),
), - wyznaczenie przedziałów wypukłości i wklęsłości oraz punktów przegięcia funkcji (badanie drugiej pochodnej funkcji: rozwiązanie równania
 oraz nierówności
oraz nierówności  i
i 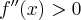 ),
), - zestawienie uzyskanych wyników w tabeli i sporządzenie na tej podstawie wykresu funkcji.
