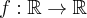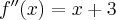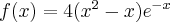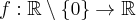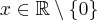Rachunek różniczkowy funkcji jednej zmiennej

Dokończ poprawnie zdanie wybierając jedną z odpowiedzi.

Zastanów się nad wypukłością/wklęsłością przedstawionych funkcji na poszczególnych przedziałach dziedziny.

Dokończ zdanie wybierając poprawne odpowiedzi.

Uzupełnij luki.

Druga pochodna funkcji $f :\mathbb{R}\to\mathbb{R}$ dana jest wzorem $f''(x)=x+3$.

Dany jest wykres drugiej pochodnej funkcji $f(x)=4(x^2-x)e^{-x}$. Dopasuj własności: wypukła/wklęsła do poszczególnych fragmentów wykresu.

Druga pochodna funkcji $f:\mathbb{R}\setminus\{0\}\to\mathbb{R}$ jest dodatnia dla $x\in\mathbb{R}\setminus\{0\}$. Zastanów się, czy funkcja może mieć wykres przedstawiony poniżej.

Połącz w pary: wzór i własność funkcji.

Przyciągnij wzory do własności.

Połącz w pary: wykres i własność funkcji.

Druga pochodna funkcji $f$ jest ujemna w całej dziedzinie. Zastanów się, czy funkcja może mieć wykres przedstawiony poniżej.