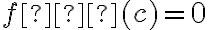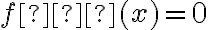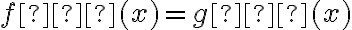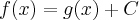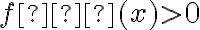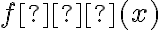Rolle'a
Lagrange'a
Iloraz  równy jest tangensowi kąta
równy jest tangensowi kąta  nachylenia prostej (siecznej) przechodzącej przez punkty
nachylenia prostej (siecznej) przechodzącej przez punkty 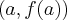 i
i 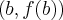 .
.
Z twierdzenie Lagrange'a wnioskujemy, że na wykresie funkcji  znajduje się przynajmniej jeden taki punkt (o odciętej
znajduje się przynajmniej jeden taki punkt (o odciętej 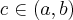 ), w którym styczna do wykresu funkcji
), w którym styczna do wykresu funkcji  jest równoległa do prostej przechodzącej przez punkty
jest równoległa do prostej przechodzącej przez punkty 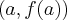 i
i 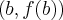 .
.
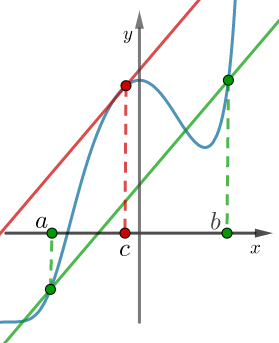
Wnioski z twierdzenia Lagrange'a
2
Implikacje odwrotne do podanych we wniosku 3 i wniosku 4 nie zachodzą, tzn. nie nie jest prawdą, np. że jeżeli  jest funkcją rosnącą na przedziale
jest funkcją rosnącą na przedziale  , to
, to  dla każdego
dla każdego  . Przykładem jest funkcja
. Przykładem jest funkcja  , która jest ściśle rosnąca, ale jej pochodna
, która jest ściśle rosnąca, ale jej pochodna  zeruje się w punkcie
zeruje się w punkcie 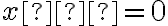 .
.

![[a,b] [a,b]](https://port.edu.p.lodz.pl/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.png)