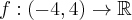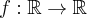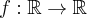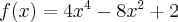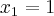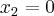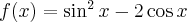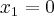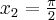Przypomnij sobie: definicje ekstremów lokalnych, warunek konieczny istnienia ekstremum lok., I warunek wystarczający, II warunek wystarczający
Przypomnij sobie: • definicje ekstremów lokalnych • warunek konieczny istnienia ekstremum lok. • I warunek wystarczający • II warunek wystarczający
1
2
Przyporządkuj podane funkcje do odpowiedniej grupy.
Przeciągnij poprawne odpowiedzi w odpowiednie pola.
3
4
5
6
7
8
9