7. Pochodna w zastosowaniach praktycznych
Przykłady
Przykład 1
Stacja orbitalna porusza się prostoliniowo na wysokości 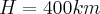 nad Ziemią z prędkością
nad Ziemią z prędkością 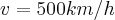 . Antena odbierająca sygnały znajduje się bezpośrednio pod trajektorią stacji. W każdej chwili oś anteny jest skierowana na stację, Jaka jest prędkość kątowa anteny w chwili, gdy stacja znajduje się w odległości
. Antena odbierająca sygnały znajduje się bezpośrednio pod trajektorią stacji. W każdej chwili oś anteny jest skierowana na stację, Jaka jest prędkość kątowa anteny w chwili, gdy stacja znajduje się w odległości 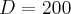 km od anteny?
km od anteny?
Rozwiązanie:
Jeśli współrzędna kątowa ciała określa kąt 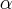 , to wartość prędkości kątowej
, to wartość prędkości kątowej 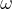 jest równa:
jest równa:
Wyznaczamy zatem kąt 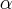 . Zauważmy, że
. Zauważmy, że
Stąd
Zatem
Po podstawieniu danych otrzymujemy, że prędkość kątowa anteny w chwili, gdy stacja znajduje się w odległości 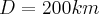 od anteny wynosi
od anteny wynosi
Przykład 4
Stół bilardowy ma następujący kształt (bandy są w kształcie parabol). Gracz ma
możliwość ustawienia bili w dowolnym miejscu na linii łączącej wierzchołki parabol. Jego zadanie polega na traeniu do pokazanego otworu przy wykorzystaniu dokładnie jednego odbicia od bandy. Zakładając, że ustawił bilę w konkretnym miejscu, w którym kierunku powinien uderzyć?
Przykład 5
z zerami
bez zer

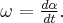
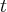
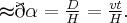
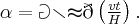
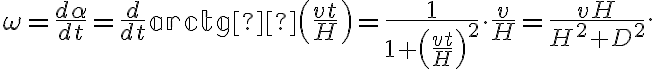
![\omega =1\ \left[\frac{\text{rad}}{h}\right]. \omega =1\ \left[\frac{\text{rad}}{h}\right].](https://port.edu.p.lodz.pl/filter/tex/pix.php/721b0700d27112f19ea4b0ab2711f840.png)