Pochodna funkcji jednej zmiennej

Przykład 2

Obliczymy granice funkcji

(a) $\lim\limits_{x\rightarrow \infty } \, x^2\,e^{-x}$,

(b)

(c)

Rozwiązanie

Zaczynamy od określenia symbolu badanej granicy funkcji:

$\lim\limits_{x\rightarrow \infty }\,x^2 \,e^{-x}= \left[ \infty\cdot0 \,\right]$.

W tym przypadku, aby zastosować regułę de l'Hospitala należy zapisać funkcję w postaci ilorazu:

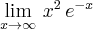
$=\lim\limits_{x\rightarrow \infty } \dfrac{x^2}{e^x}=\left[ \frac{\infty}{\infty} \right]$

$\text{Dalej, dwukrotnie stosując regułę de l'Hospitala, otrzymujemy}$

$\lim\limits_{x\rightarrow \infty } \dfrac{x^2}{e^x}\overset{\text{H}}{=} \lim\limits_{x\rightarrow \infty } \dfrac{(x^2)'}{(e^x)'} = \lim\limits_{x\rightarrow \infty }\,\dfrac{2x}{e^x} = \left[ \frac{\infty}{\infty} \right]\overset{\text{H}}{=} \lim\limits_{x\rightarrow \infty }\,\dfrac{(2x)'}{(e^x)'} = \lim\limits_{x\rightarrow \infty }\,\dfrac{2}{e^x} = 0$