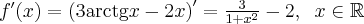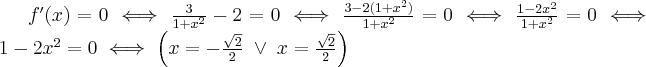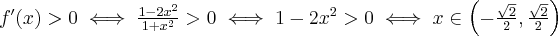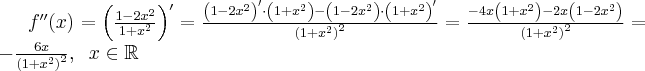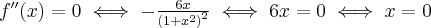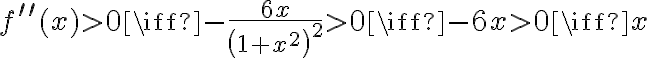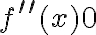6. Badanie przebiegu zmienności funkcji
Przykłady
Przykład 1
Zbadamy przebieg zmienności funkcji  .
.
Rozwiązanie
1. Dziedziną funkcji  jest zbiór
jest zbiór 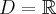 .
.
2. Obliczamy granice w punktach brzegowych dziedziny i wyznaczamy asymptoty funkcji  :
:
Zatem prosta o równaniu  jest asymptotą poziomą funkcji w
jest asymptotą poziomą funkcji w 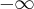 i
i 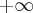 .
.
Funkcja nie ma asymptot pionowych.
3. Wyznaczymy ekstrema i przedziały monotoniczności funkcji  . Obliczamy w tym celu pochodną funkcji.
. Obliczamy w tym celu pochodną funkcji.
Wyznaczymy punkty stacjonarne funkcji:
Punkt ten należy do dziedziny funkcji.
Wyznaczymy teraz przedziały monotoniczności funkcji. Zauważmy najpierw, że  dla każdego
dla każdego  , zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia  . Mamy więc:
. Mamy więc:
Uwzględniając dziedzinę funkcji wnioskujemy, że funkcja jest malejąca na przedziale  , rosnąca na przedziale
, rosnąca na przedziale 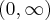 .
.
Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie  funkcja ma minimum lokalne, przy czym
funkcja ma minimum lokalne, przy czym  .
.
4. Wyznaczymy przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji  . Obliczamy w tym celu drugą pochodną funkcji.
. Obliczamy w tym celu drugą pochodną funkcji.
Wyznaczymy wartości  , dla których funkcja może mieć punkt przegięcia:
, dla których funkcja może mieć punkt przegięcia:
Obie wartości  należą do dziedziny funkcji.
należą do dziedziny funkcji.
Zauważmy, że  dla każdego
dla każdego  , zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia 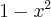 .
.
Wyznaczymy przedziały wypukłości i wklęsłości funkcji:
Dziedziną funkcji jest zbiór  , stąd funkcja jest wypukła na przedziale
, stąd funkcja jest wypukła na przedziale  , wklęsła na przedziałach
, wklęsła na przedziałach  ,
, 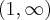 . Punkty
. Punkty  ,
, 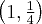 są punktami przegięcia funkcji.
są punktami przegięcia funkcji.
5. Tabelka przebiegu zmienności funkcji  .
.
Przykład 2
Zbadamy przebieg zmienności funkcji  .
.
1. Dziedziną funkcji  jest zbiór
jest zbiór 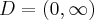 .
.
2. Obliczamy granice w punktach brzegowych dziedziny i wyznaczamy asymptoty funkcji  :
:
![\lim\limits_{x\to 0^+} \frac{4+\ln x}{x}=\left[\frac{4+\ln 0^+}{0^+}=\frac{4-\infty}{0^+}=-\infty\cdot \infty\right]=-\infty. \lim\limits_{x\to 0^+} \frac{4+\ln x}{x}=\left[\frac{4+\ln 0^+}{0^+}=\frac{4-\infty}{0^+}=-\infty\cdot \infty\right]=-\infty.](https://port.edu.p.lodz.pl/filter/tex/pix.php/e40cef26f855a72afe259a6f825beb13.png) Zatem funkcja ma asymptotę pionową prawostronną
Zatem funkcja ma asymptotę pionową prawostronną  ,
,
Zatem prosta o równaniu 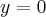 jest asymptotą poziomą funkcji
jest asymptotą poziomą funkcji  w
w 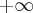 .
.
3. Wyznaczymy ekstrema i przedziały monotoniczności funkcji  . Obliczamy w tym celu pochodną funkcji.
. Obliczamy w tym celu pochodną funkcji.
Wyznaczymy punkty stacjonarne funkcji:
Punkt ten należy do dziedziny funkcji.
Wyznaczymy teraz przedziały monotoniczności funkcji. Zauważmy najpierw, że  dla każdego
dla każdego 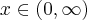 , zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia  . Mamy więc:
. Mamy więc:
Uwzględniając dziedzinę funkcji wnioskujemy, że funkcja jest rosnąca na przedziale  , malejąca na przedziale
, malejąca na przedziale 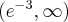 .
.
Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie  funkcja ma maksimum lokalne, przy czym
funkcja ma maksimum lokalne, przy czym 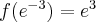 .
.
4. Wyznaczymy przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji  . Obliczamy w tym celu drugą pochodną funkcji.
. Obliczamy w tym celu drugą pochodną funkcji.
Wyznaczymy wartości  , dla których funkcja może mieć punkt przegięcia.
, dla których funkcja może mieć punkt przegięcia.
Wyznaczona wartość  należy do dziedziny funkcji.
należy do dziedziny funkcji.
Zauważmy, że  dla każdego
dla każdego 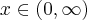 , zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia 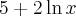 .
.
Wyznaczymy przedziały wypukłości i wklęsłości funkcji  :
:
Uwzględniając dziedzinę funkcji otrzymujemy, że funkcja  jest wklęsła na przedziale
jest wklęsła na przedziale  , wypukła na przedziale
, wypukła na przedziale 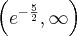 , punkt
, punkt 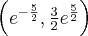 jest punktem przegięcia funkcji.
jest punktem przegięcia funkcji.
5. Tabelka przebiegu zmienności funkcji
6. Wykres funkcji
Przykład 3
Zbadamy przebieg zmienności funkcji 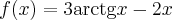 .
.
1. Dziedziną funkcji  jest zbiór
jest zbiór  .
.
2. Obliczamy granice w punktach brzegowych dziedziny i wyznaczamy asymptoty funkcji  :
:
Funkcja nie ma asymptot pionowych.
Asymptoty ukośne ( ) - mogą istnieć w nieskończonych krańcach dziedziny funkcji. W
) - mogą istnieć w nieskończonych krańcach dziedziny funkcji. W 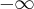 mamy:
mamy:
Zatem prosta o równaniu  jest asymptotą ukośną funkcji w
jest asymptotą ukośną funkcji w 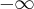 .
.
Zatem prosta o równaniu  jest asymptotą ukośną funkcji w
jest asymptotą ukośną funkcji w 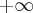 .
.
Podsumowując otrzymujemy, że prosta o równaniu  jest asymptotą ukośną funkcji w
jest asymptotą ukośną funkcji w 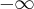 , prosta prosta o równaniu
, prosta prosta o równaniu  jest asymptotą ukośną funkcji w
jest asymptotą ukośną funkcji w 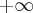 .
.
3. Wyznaczymy ekstrema i przedziały monotoniczności funkcji  . Obliczamy w tym celu pochodną funkcji.
. Obliczamy w tym celu pochodną funkcji.
Wyznaczymy punkty stacjonarne funkcji.
Każdy z wyznaczonych punktów należy do dziedziny funkcji.
Wyznaczymy teraz przedziały monotoniczności funkcji. Zauważmy najpierw, że 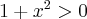 dla każdego
dla każdego  , zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia 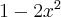 . Mamy więc:
. Mamy więc:
Zatem funkcja jest malejąca na każdym z przedziałów  ,
, 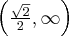 , rosnąca na przedziale
, rosnąca na przedziale  . Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie
. Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie 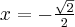 funkcja ma minimum lokalne, przy czym
funkcja ma minimum lokalne, przy czym 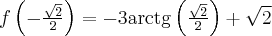 .
.
W punkcie  funkcja ma maksimum lokalne, przy czym
funkcja ma maksimum lokalne, przy czym 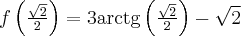 .
.
4. Wyznaczymy przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji  . Obliczamy w tym celu drugą pochodną funkcji.
. Obliczamy w tym celu drugą pochodną funkcji.
Wyznaczymy wartości  , dla których funkcja może mieć punkt przegięcia.
, dla których funkcja może mieć punkt przegięcia.
Wyznaczona wartość  należy do dziedziny funkcji.
należy do dziedziny funkcji.
Zauważmy, że  dla każdego
dla każdego  , zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia 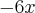 .
.
Wyznaczymy przedziały wypukłości i wklęsłości funkcji:
Zatem funkcja  jest wypukła na przedziale
jest wypukła na przedziale  , wklęsła na przedziale
, wklęsła na przedziale 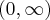 , w punkcie
, w punkcie  funkcja ma punkt przegięcia.
funkcja ma punkt przegięcia.
5. Tabelka przebiegu zmienności funkcji
6. Wykres funkcji


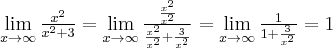

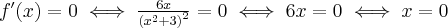
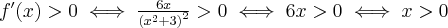

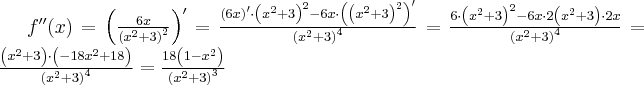
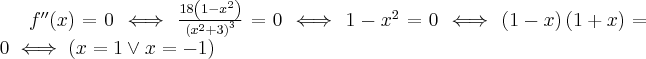


![\lim\limits_{x\to \infty} \frac{4+\ln x}{x}=\left[\frac{\infty}{\infty}\right]\stackrel{[H]}{=}\lim\limits_{x\to \infty}\frac{\frac1x}{1}=\lim\limits_{x\to \infty}\frac{1}{x}=\left[\frac{1}{\infty}\right]=0 \lim\limits_{x\to \infty} \frac{4+\ln x}{x}=\left[\frac{\infty}{\infty}\right]\stackrel{[H]}{=}\lim\limits_{x\to \infty}\frac{\frac1x}{1}=\lim\limits_{x\to \infty}\frac{1}{x}=\left[\frac{1}{\infty}\right]=0](https://port.edu.p.lodz.pl/filter/tex/pix.php/e4e335ef4c0c50ee92ee09902a516539.png)
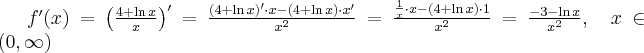
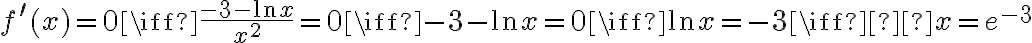
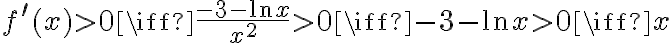
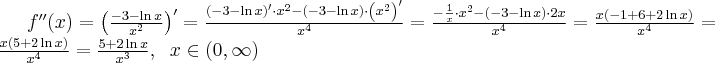
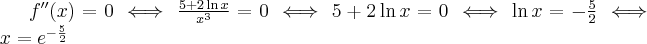
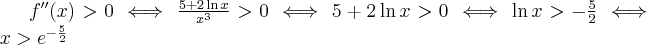
![\lim\limits_{x\to -\infty} f(x)=\lim\limits_{x\to -\infty}\left(3\mathrm{arctg}x-2x\right)=\left[{3\mathrm{arctg}(-\infty)-2\cdot(-\infty)=\frac {-3\pi}{2}}+\infty\right]=\infty \lim\limits_{x\to -\infty} f(x)=\lim\limits_{x\to -\infty}\left(3\mathrm{arctg}x-2x\right)=\left[{3\mathrm{arctg}(-\infty)-2\cdot(-\infty)=\frac {-3\pi}{2}}+\infty\right]=\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/a40f617bfa6e4eac6b62c45cf68eae56.png)
![\lim\limits_{x\to \infty} f(x)=\lim\limits_{x\to \infty}\left(3\mathrm{arctg}x-2x\right)=\left[{3\mathrm{arctg}(\infty)-2\cdot\infty=\frac {3\pi}{2}}-\infty\right]=-\infty \lim\limits_{x\to \infty} f(x)=\lim\limits_{x\to \infty}\left(3\mathrm{arctg}x-2x\right)=\left[{3\mathrm{arctg}(\infty)-2\cdot\infty=\frac {3\pi}{2}}-\infty\right]=-\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/9938b301a6c3ca5fa507ad2b403a46e6.png)
![\lim\limits_{x\to -\infty}\frac{f(x)}{x}= \lim\limits_{x\to -\infty}\frac{3\mathrm{arctg}x-2x}{x}=\lim\limits_{x\to -\infty} \frac{3\mathrm{arctg}x}{x}-2=\left[\frac{3\mathrm{arctg}(-\infty)}{-\infty}-2=\frac{-\frac {3\pi}{2}}{-\infty}-2\right]=-2 \Rightarrow a=-2\text{ w }-\infty \lim\limits_{x\to -\infty}\frac{f(x)}{x}= \lim\limits_{x\to -\infty}\frac{3\mathrm{arctg}x-2x}{x}=\lim\limits_{x\to -\infty} \frac{3\mathrm{arctg}x}{x}-2=\left[\frac{3\mathrm{arctg}(-\infty)}{-\infty}-2=\frac{-\frac {3\pi}{2}}{-\infty}-2\right]=-2 \Rightarrow a=-2\text{ w }-\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/2015f910017aaf81bc5d8e9ea3319dac.png)
![\lim\limits_{x\to -\infty}(f(x)-ax)=\lim\limits_{x\to -\infty} \left(3\mathrm{arctg}x-2x-(-2x)\right)=\lim\limits_{x\to -\infty} 3\mathrm{arctg}x=\left[3\mathrm{arctg}(-\infty)\right]=\frac {-3\pi}{2}\Rightarrow b=\frac {-3\pi}{2}\text{ w }-\infty \lim\limits_{x\to -\infty}(f(x)-ax)=\lim\limits_{x\to -\infty} \left(3\mathrm{arctg}x-2x-(-2x)\right)=\lim\limits_{x\to -\infty} 3\mathrm{arctg}x=\left[3\mathrm{arctg}(-\infty)\right]=\frac {-3\pi}{2}\Rightarrow b=\frac {-3\pi}{2}\text{ w }-\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/8a3bf2ec05d99889575a8e9284aa3a96.png)
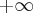
![\lim\limits_{x\to \infty}\frac{f(x)}{x}= \lim\limits_{x\to \infty}\frac{3\mathrm{arctg}x-2x}{x}=\lim\limits_{x\to \infty} \frac{3\mathrm{arctg}x}{x}-2=\left[\frac{3\mathrm{arctg}(\infty)}{\infty}-2=\frac{\frac {3\pi}{2}}{\infty}-2\right]=-2 \Rightarrow a=-2\text{ w }+\infty \lim\limits_{x\to \infty}\frac{f(x)}{x}= \lim\limits_{x\to \infty}\frac{3\mathrm{arctg}x-2x}{x}=\lim\limits_{x\to \infty} \frac{3\mathrm{arctg}x}{x}-2=\left[\frac{3\mathrm{arctg}(\infty)}{\infty}-2=\frac{\frac {3\pi}{2}}{\infty}-2\right]=-2 \Rightarrow a=-2\text{ w }+\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/ef292a92df718370d6fd4f25f15bd7c0.png)
![\lim\limits_{x\to \infty}(f(x)-ax)=\lim\limits_{x\to \infty} \left(3\mathrm{arctg}x-2x-(-2x)\right)=\lim\limits_{x\to \infty} 3\mathrm{arctg}x=\left[3\mathrm{arctg}(\infty)\right]=\frac {3\pi}{2}\Rightarrow b=\frac {3\pi}{2}\text{ w }+\infty \lim\limits_{x\to \infty}(f(x)-ax)=\lim\limits_{x\to \infty} \left(3\mathrm{arctg}x-2x-(-2x)\right)=\lim\limits_{x\to \infty} 3\mathrm{arctg}x=\left[3\mathrm{arctg}(\infty)\right]=\frac {3\pi}{2}\Rightarrow b=\frac {3\pi}{2}\text{ w }+\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/5eba63ad417b92221ef227f2511832a1.png)