Rachunek różniczkowy funkcji jednej zmiennej

Funkcja ciągła na przedziale domkniętym $[a,b]$ osiąga w tym przedziale swoją wartość największą i wartość najmniejszą (wynika to z twierdzenia Weierstrassa). Wartości: największą i najmniejszą funkcji na przedziale domkniętym nazywamy ekstremami globalnymi (absolutnymi): odpowiednio maksimum globalnym (absolutnym) i minimum globalnym (absolutnym).

Ekstremum globalne może być osiągnięte wewnątrz przedziału (jest wtedy jednocześnie ekstremum lokalnym) lub w punkcie brzegowym przedziału.

Metoda wyznaczania ekstremów globalnych funkcji ciągłej $f$ na przedziale domkniętym $[a,b]$ jest następująca:

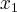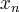1.  w przedziale $(a,b)$ znajdujemy punkty $x_1$, $\ldots$, $x_n$, w których funkcja może mieć ekstrema lokalne, czyli punkty będące rozwiązaniami równania $f^\prime(x)=0$ lub punkty, w których pochodna nie istnieje,

2. obliczamy wartości funkcji w punktach: 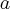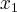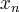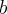$a$, $x_1$, $\ldots$, $x_n$, $b$, czyli

$f(a)$, $f(x_1)$, $\ldots$, $f(x_n)$, $f(b)$,

3. największa z liczb 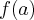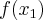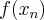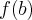$f(a)$, $f(x_1)$, $\ldots$, $f(x_n)$, $f(b)$ jest maksimum globalnym, a najmniejsza - minimum globalnym funkcji $f$ na przedziale domkniętym $[a,b]$.