Rachunek różniczkowy funkcji jednej zmiennej

Definicja 

Załóżmy, że funkcja $f$ jest określona i ciągła na pewnym otoczeniu punktu $x_{0}$. Styczną do wykresu funkcji $f$ w punkcie $x_{0}$ (w punkcie wykresu $(x_{0}$, $f(x_{0}))$) nazywamy prostą będącą granicznym położeniem siecznych wykresu funkcji $f$ przechodzących przez punkty $(x_{0},f(x_{0}))$ i $(x, f(x))$, gdy $x\rightarrow x_{0}$.

RYSUNEK

Iloraz różnicowy 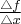$\frac{\triangle f}{\triangle x}$ równy jest tangensowi kąta $\alpha _{s}$ nachylenia prostej (siecznej) przechodzącej przez punkty $A=(x_{0},f(x_{0}))$ i $B=(x_{0}+\triangle x,f(x_{0}+\triangle x))$:

$\frac{\triangle f}{\triangle x}=\text{tg}\alpha _{s}.$

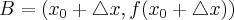Jeżeli granica 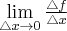$\lim\limits_{\triangle x\rightarrow 0}\frac{\triangle f}{ \triangle x}$ istnieje i jest skończona, to jej wartość równa jest tangensowi kąta $\alpha$ nachylenia stycznej do wykresu funkcji $f$ poprowadzonej w punkcie $A$, zatem

$f^{\prime }(x_{0})=\text{tg}\alpha$.

RYSUNEK

Pochodna $f^{\prime }(x_{0})$ jest równa współczynnikowi kierunkowemu stycznej do wykresu funkcji $f$ poprowadzonej w punkcie $(x_{0},f(x_{0}))$.

Twierdzenie 3 -- o równaniu stycznej do wykresu funkcji

Niech funkcja $f$ będzie określona w otoczeniu punktu $x_{0}$ i posiada pochodną (właściwą) w punkcie $x_{0}$. Równanie stycznej do wykresu funkcji $f$ w punkcie $x_{0}$ ma postać

$y-f(x_{0})=f^{\prime }(x_{0})(x-x_{0})$.