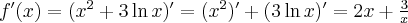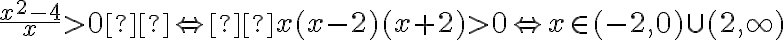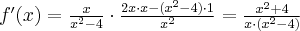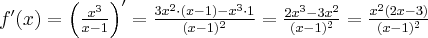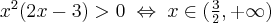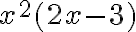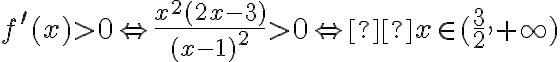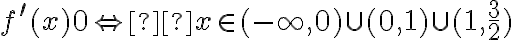4.1 Badanie monotoniczności funkcji (*)
Przykłady
1
Wykażemy, że funkcja określona wzorem 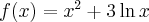 jest monotoniczna w całej dziedzinie.
jest monotoniczna w całej dziedzinie.
Funkcja  jest określona na zbiorze
jest określona na zbiorze  . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
Ponieważ 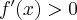 dla
dla  , więc funkcja
, więc funkcja  jest rosnąca w całej swojej dziedzinie.
jest rosnąca w całej swojej dziedzinie.
Film
2
Wyznaczymy przedziały monotoniczności funkcji określonej wzorem 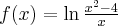 .
.
Aby wyznaczyć dziedzinę funkcji  należy rozwiązać nierówność
należy rozwiązać nierówność 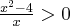 . Ponieważ
. Ponieważ
zatem 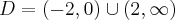 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
Zauważamy, że pochodna funkcji jest dodatnia w całej dziedzinie. Nie oznacza to jednak, że funkcja jest rosnąca w całej dziedzinie, gdyż dziedzina nie jest przedziałem a sumą przedziałów. A zatem stwierdzamy, że funkcja  jest rosnąca na przedziale
jest rosnąca na przedziale 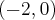 i na przedziale
i na przedziale 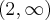 .
.
3
Wyznaczymy przedziały monotoniczności funkcji określonej wzorem 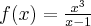 .
.
W tym przypadku 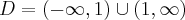 . Obliczamy pochodną funkcji
. Obliczamy pochodną funkcji  :
:
Aby wyznaczyć przedziały monotoniczności funkcji  badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Ponieważ
badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Ponieważ 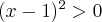 dla każdego
dla każdego 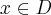 oraz
oraz
więc
A zatem badana funkcja jest rosnąca na przedziale 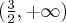 oraz malejąca na każdym z przedziałów
oraz malejąca na każdym z przedziałów 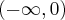 ,
, 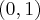 i
i 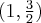 .
.
4.
Wyznaczymy przedziały monotoniczności funkcji określonej wzorem 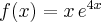 .
.