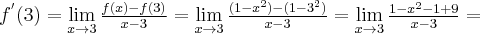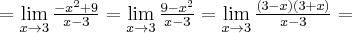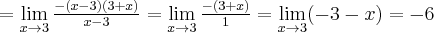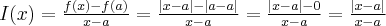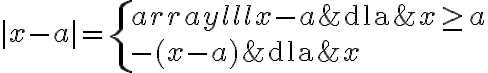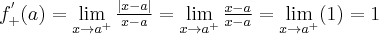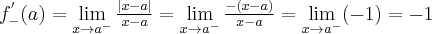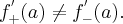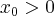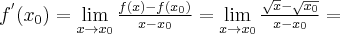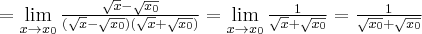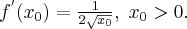1.1 Pochodna funkcji w punkcie

Przykłady

Przykład 1

Korzystając z definicji obliczymy pochodną funkcji 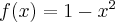f(x)=1-x^{2} w punkcie x_{0}=3.

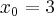Rozwiązanie

f^{^{\prime }}(3)=\lim\limits_{x\rightarrow 3}\frac{f(x)-f(3)}{x-3} =\lim\limits_{x\rightarrow 3}\frac{(1-x^{2})-(1-3^{2})}{x-3} =\lim\limits_{x\rightarrow 3}\frac{1-x^{2}-1+9}{x-3}=

=\lim\limits_{x\rightarrow 3}\frac{-x^{2}+9}{x-3}=\lim\limits_{x\rightarrow 3}\frac{9-x^{2}}{x-3}=\lim\limits_{x\rightarrow 3}\frac{(3-x)(3+x)}{x-3}=

=\lim\limits_{x\rightarrow 3}\frac{-(x-3)(3+x)}{x-3}=\lim\limits_{x \rightarrow 3}\frac{-(3+x)}{1}=\lim\limits_{x\rightarrow 3}(-3-x)=-6.

Przykład 2

Obliczymy pochodne jednostronne funkcji 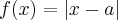f(x)=|x-a| w punkcie 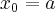x_{0}=a, gdzie a\in \mathbb{R}.

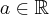Rozwiązanie

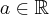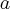Niech a\in \mathbb{R}. Iloraz różnicowy funkcji f w punkcie a ma postać:

I(x)=\frac{f(x)-f(a)}{x-a}=\frac{|x-a|-|a-a|}{x-a}=\frac{|x-a|-0}{x-a}=\frac{ |x-a|}{x-a}.

Korzystając z definicji modułu mamy:

|x-a|=\left\{ \begin{array}{lll} x-a & \text{dla} & x\geq a \\ -(x-a) & \text{dla} & x.

Obliczymy teraz pochodne jednostronne w punkcie 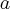a:

f_{+}^{^{\prime }}(a)=\lim\limits_{x\rightarrow a^{+}}\frac{|x-a|}{x-a} =\lim\limits_{x\rightarrow a^{+}}\frac{x-a}{x-a}=\lim\limits_{x\rightarrow a^{+}}(1)=1,

f_{-}^{^{\prime }}(a)=\lim\limits_{x\rightarrow a^{-}}\frac{|x-a|}{x-a} =\lim\limits_{x\rightarrow a^{-}}\frac{-(x-a)}{x-a}=\lim\limits_{x \rightarrow a^{-}}(-1)=-1.

Zauważmymy, że

f_{+}^{^{\prime }}(a)\not=f_{-}^{^{\prime }}(a)\text{.}

Zatem nie istnieje pochodna funkcji f w punkcie x_{0}=a.

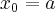Przykład 3

Obliczymy pochodną funkcji f(x)=\sqrt{x} w dowolnym punkcie x_{0}>0.

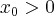Rozwiązanie

Niech x_0 >0.

f^{^{\prime }}(x_{0})=\lim\limits_{x\rightarrow x_{0}}\frac{f(x)-f(x_{0})}{ x-x_{0}}=\lim\limits_{x\rightarrow x_{0}}\frac{\sqrt{x}-\sqrt{x_{0}}}{x-x_{0} }=

=\lim\limits_{x\rightarrow x_{0}}\frac{\sqrt{x}-\sqrt{x_{0}}}{(\sqrt{x}- \sqrt{x_{0}})(\sqrt{x}+\sqrt{x_{0}})}=\lim\limits_{x\rightarrow x_{0}}\frac{1 }{\sqrt{x}+\sqrt{x_{0}}}=\frac{1}{\sqrt{x_{0}}+\sqrt{x_{0}}}.

Czyli

f^{^{\prime }}(x_{0})=\frac{1}{2\sqrt{x_{0}}}, \; x_0>0\text{.}