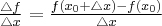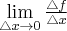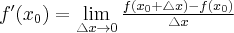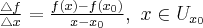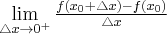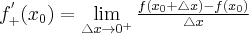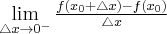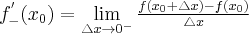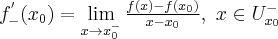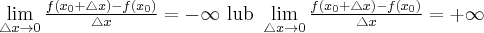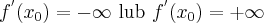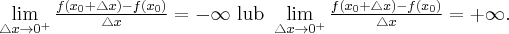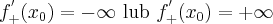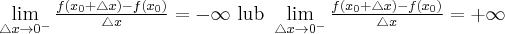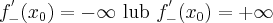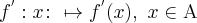1.1 Pochodna funkcji w punkcie
Teoria
Definicja
Załóżmy, że funkcja  jest określona na pewnym otoczeniu
jest określona na pewnym otoczeniu  punktu
punktu  . Niech
. Niech 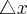 będzie różnym od zera przyrostem zmiennej
będzie różnym od zera przyrostem zmiennej  takim, że
takim, że 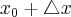 należy do tego otoczenia. Niech
należy do tego otoczenia. Niech 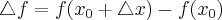 będzie przyrostem wartości funkcji odpowiadającym przyrostowi
będzie przyrostem wartości funkcji odpowiadającym przyrostowi 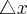 . Ilorazem różnicowym funkcji
. Ilorazem różnicowym funkcji  w punkcie
w punkcie  dla przyrostu
dla przyrostu 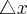 nazywamy wyrażenie
nazywamy wyrażenie
Jeżeli istnieje i jest skończona granica
to nazywamy ją pochodną funkcji  w punkcie
w punkcie  i oznaczamy
i oznaczamy  lub
lub  . Zatem
. Zatem
(o ile granica ta istnieje i jest skończona).
FILM
Funkcję jednej zmiennej, która ma pochodną w punkcie  nazywamy funkcją różniczkowalną w tym punkcie.
nazywamy funkcją różniczkowalną w tym punkcie.
Uwaga
Iloraz różnicowy może być także zapisany w postaci
Wówczas pochodna funkcji  w punkcie
w punkcie  ma postać
ma postać
Definicja
Załóżmy, że funkcja  jest określona na pewnym prawostronnym otoczeniu
jest określona na pewnym prawostronnym otoczeniu  . Niech
. Niech 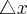 będzie różnym od zera przyrostem zmiennej
będzie różnym od zera przyrostem zmiennej  takim, że
takim, że 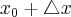 należy do tego otoczenia. Niech
należy do tego otoczenia. Niech 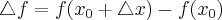 będzie przyrostem funkcji odpowiadającym przyrostowi
będzie przyrostem funkcji odpowiadającym przyrostowi 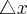 . Jeżeli istnieje i jest skończona granica
. Jeżeli istnieje i jest skończona granica
to nazywamy ją pochodną prawostronną funkcji  w punkcie
w punkcie  i oznaczamy
i oznaczamy 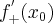 lub
lub  . Zatem
. Zatem
Uwaga
Pochodna prawostronna funkcji  w punkcie
w punkcie  może być także zapisana w postaci
może być także zapisana w postaci
Definicja
Załóżmy, że funkcja  jest określona na pewnym lewostronnym otoczeniu
jest określona na pewnym lewostronnym otoczeniu  . Niech
. Niech 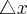 będzie różnym od zera przyrostem zmiennej
będzie różnym od zera przyrostem zmiennej  takim, że
takim, że 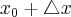 należy do tego otoczenia. Niech
należy do tego otoczenia. Niech 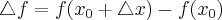 będzie przyrostem funkcji odpowiadającym przyrostowi
będzie przyrostem funkcji odpowiadającym przyrostowi 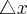 . Jeżeli istnieje i jest skończona granica
. Jeżeli istnieje i jest skończona granica
to nazywamy ją pochodną lewostronną funkcji  w punkcie
w punkcie  i oznaczamy
i oznaczamy  . Zatem
. Zatem
Uwaga
Pochodna lewostronna funkcji  w punkcie
w punkcie  może być także zapisana w postaci
może być także zapisana w postaci
Twierdzenie 1 - warunek konieczny i wystarczający istnienia pochodnej w punkcie
Funkcja  ma pochodną w punkcie
ma pochodną w punkcie  wtedy i tylko wtedy, gdy istnieją i są sobie równe pochodne jednostronne funkcji
wtedy i tylko wtedy, gdy istnieją i są sobie równe pochodne jednostronne funkcji  w punkcie
w punkcie  . Wówczas
. Wówczas
Definicja
Załóżmy, że funkcja  jest określona i ciągła na pewnym otoczeniu punktu
jest określona i ciągła na pewnym otoczeniu punktu  . Mówimy, że funkcja
. Mówimy, że funkcja  ma pochodną niewłaściwą w punkcie
ma pochodną niewłaściwą w punkcie  , gdy
, gdy
Wówczas piszemy
Definicja
Załóżmy, że funkcja  jest określona i ciągła na pewnym prawostronnym otoczeniu punktu
jest określona i ciągła na pewnym prawostronnym otoczeniu punktu  . Mówimy, że funkcja
. Mówimy, że funkcja  ma pochodną niewłaściwą prawostronną w punkcie
ma pochodną niewłaściwą prawostronną w punkcie  , gdy
, gdy
Wówczas piszemy
Definicja
Załóżmy, że funkcja  jest określona i ciągła na pewnym lewostronnym otoczeniu punktu
jest określona i ciągła na pewnym lewostronnym otoczeniu punktu  . Mówimy, że funkcja
. Mówimy, że funkcja  ma pochodną niewłaściwą lewostronną w punkcie
ma pochodną niewłaściwą lewostronną w punkcie  , gdy
, gdy
Wówczas piszemy
Definicja
Załóżmy, że funkcja  jest określona na zbiorze
jest określona na zbiorze  . Jeżeli
. Jeżeli  ma pochodną w każdym punkcie zbioru
ma pochodną w każdym punkcie zbioru 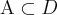 , to funkcję
, to funkcję
nazywamy funkcją pochodną lub pochodną funkcji  na zbiorze
na zbiorze 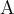 .
.
Twierdzenie
Załóżmy, że funkcja  jest określona na pewnym otoczeniu punktu
jest określona na pewnym otoczeniu punktu  . Jeżeli
. Jeżeli  jest różniczkowalna w punkcie
jest różniczkowalna w punkcie  , to jest ciągła w tym punkcie.
, to jest ciągła w tym punkcie.
Uwaga
Implikacja odwrotna nie zachodzi, tzn. nie jest prawdą, że jeżeli funkcja jest ciągła w punkcie  , to jest różniczkowalna w tym punkcie. Przykładem funkcji, która jest ciągła i nieróżniczkowalna w
, to jest różniczkowalna w tym punkcie. Przykładem funkcji, która jest ciągła i nieróżniczkowalna w  jest
jest  .
.