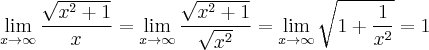2.2 Reguła de l'Hospitala (*)
Przykłady
Przykład 1
Obliczymy granice funkcji:
a) Zaczynamy od określenia symbolu granicy, aby zdecydować, czy można zastosować regułę de l'Hospitala.
Następnie badamy, czy istnieje granica ilorazu pochodnych:
Na mocy reguły de l'Hospitala otrzymujemy odpowiedź
Zwykle stosując regułę de l'Hospitala stosujemy uproszczony zapis, przedstawiony w rozwiązaniu kolejnego zadania.
c) Określamy symbol badanej granicy:
Symbol granicy jest oznaczony, a zatem w tym przypadku nie można wykorzystać reguły de l'Hospitala. Aby obliczyć granicę należy zastosować odpowiednie twierdzenia arytmetyki granic funkcji:
Na koniec zauważmy, że w tym przypadku
a zatem granica ilorazu pochodnych różni się od badanej granicy.
Przykład 2
Obliczymy granice funkcji:
b) W przypadku tej granicy regułę de l'Hospitala zastosujemy dwukrotnie:
Wykorzystaliśmy tutaj fakt, że  .
.
Przykład 3
Obliczymy granice funkcji:
Rozwiązanie
Podobnie jak w poprzednich przykładach zaczynamy od określenia symbolu badanej granicy
przy czym 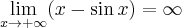 na mocy twierdzenia o dwóch ciągach.
na mocy twierdzenia o dwóch ciągach.
W tym przypadku nie możemy wykorzystać reguły de l'Hospitala, gdyż
zaś taka granica nie istnieje. Nie oznacza to jednak, że nie istnieje badana granica -- trzeba tylko policzyć ją innym sposobem. Ponieważ
więc na mocy twierdzenia o trzech ciągach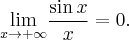
b) W tym przypadku
a zatem stosowanie reguły de l'Hospitala nie jest efektywne. Granicę funkcji możemy jednak obliczyć w inny sposób:

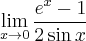
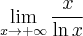
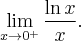

![\dfrac{e^x-1}{2\sin x} = \left[\dfrac{0}{0}\right] \dfrac{e^x-1}{2\sin x} = \left[\dfrac{0}{0}\right]](https://port.edu.p.lodz.pl/filter/tex/pix.php/3a32e8a400e82e6025c8fc27f796d3e7.png)



![\underset{x\rightarrow +\infty }{\lim }\, \dfrac{x}{\ln x} = \left[\dfrac{\infty}{\infty}\right] \overset{\text{H}}{=} \underset{x\rightarrow +\infty }{\lim }\, \dfrac{x}{\ln x} = \left[\dfrac{\infty}{\infty}\right] \overset{\text{H}}{=}](https://port.edu.p.lodz.pl/filter/tex/pix.php/f51b93dc00924ac3be8ae55eb4aec36b.png)
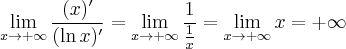
![\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\ln x }{x} = \left[\dfrac{-\infty}{0^{+}}\right]. \underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\ln x }{x} = \left[\dfrac{-\infty}{0^{+}}\right].](https://port.edu.p.lodz.pl/filter/tex/pix.php/d8ff9a271b17743a4c7cfd0f3a66f70e.png)
![\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\ln x }{x} = \underset{x\rightarrow 0^{+} }{\lim }\, \ln x \cdot \dfrac{1}{x} =\left[-\infty \cdot \dfrac{1}{0^{+}}\right] = [-\infty \cdot \infty]=-\infty. \underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\ln x }{x} = \underset{x\rightarrow 0^{+} }{\lim }\, \ln x \cdot \dfrac{1}{x} =\left[-\infty \cdot \dfrac{1}{0^{+}}\right] = [-\infty \cdot \infty]=-\infty.](https://port.edu.p.lodz.pl/filter/tex/pix.php/d9c9c4343188476654c6443e78e3ba90.png)
![\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{(\ln x)'}{(x)'} =\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\frac{1}{x}}{1} = \left[\dfrac{1}{0^{+}}\right] = +\infty , \underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{(\ln x)'}{(x)'} =\underset{x\rightarrow 0^{+} }{\lim }\, \dfrac{\frac{1}{x}}{1} = \left[\dfrac{1}{0^{+}}\right] = +\infty ,](https://port.edu.p.lodz.pl/filter/tex/pix.php/bbb5e72bdead71840570c10cc44b91cf.png)
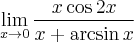
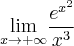
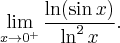
![\underset{x\rightarrow 0}{\lim }\,\dfrac{x\cos 2x}{x+\arcsin x} = \left[\dfrac{0}{0}\right]\overset{\text{H}}{=} \underset{x\rightarrow 0}{\lim }\dfrac{(x\cos 2x)'}{(x+\arcsin x)'}=\underset{x\rightarrow 0}{\lim }\,\dfrac{\cos 2x-x\sin 2x\cdot 2}{1+\frac{1}{\sqrt{1-x^{2}}}}= \underset{x\rightarrow 0}{\lim }\,\dfrac{x\cos 2x}{x+\arcsin x} = \left[\dfrac{0}{0}\right]\overset{\text{H}}{=} \underset{x\rightarrow 0}{\lim }\dfrac{(x\cos 2x)'}{(x+\arcsin x)'}=\underset{x\rightarrow 0}{\lim }\,\dfrac{\cos 2x-x\sin 2x\cdot 2}{1+\frac{1}{\sqrt{1-x^{2}}}}=](https://port.edu.p.lodz.pl/filter/tex/pix.php/10b4959c1038fb647798ed685676c5a1.png)
![\left[\dfrac{1-0}{1+1}\right]=\dfrac{1}{2}\,. \left[\dfrac{1-0}{1+1}\right]=\dfrac{1}{2}\,.](https://port.edu.p.lodz.pl/filter/tex/pix.php/14781e69ee53cceba5f856da788ecd37.png)
![\underset{x\rightarrow + \infty }{\lim }\dfrac{e^{x^{2}}}{x^{3}}=\left[ \dfrac{\infty }{\infty }\right] \overset{\text{H}}{=}\underset{x\rightarrow +\infty } {\lim }\dfrac{(e^{x^{2}})^{\prime }}{(x^{3})^{\prime }}=\underset{ x\rightarrow +\infty }{\lim }\dfrac{e^{x^{2}}\cdot 2x}{3x^{2}}=\underset{ x\rightarrow +\infty }{\lim }\dfrac{2e^{x^{2}}}{3x}=\left[ \dfrac{\infty }{\infty }\right] \overset{\text{H}}{=} \underset{x\rightarrow + \infty }{\lim }\dfrac{e^{x^{2}}}{x^{3}}=\left[ \dfrac{\infty }{\infty }\right] \overset{\text{H}}{=}\underset{x\rightarrow +\infty } {\lim }\dfrac{(e^{x^{2}})^{\prime }}{(x^{3})^{\prime }}=\underset{ x\rightarrow +\infty }{\lim }\dfrac{e^{x^{2}}\cdot 2x}{3x^{2}}=\underset{ x\rightarrow +\infty }{\lim }\dfrac{2e^{x^{2}}}{3x}=\left[ \dfrac{\infty }{\infty }\right] \overset{\text{H}}{=}](https://port.edu.p.lodz.pl/filter/tex/pix.php/5b80619ac8676c4a800681bf3a57b9d2.png)
![=\underset{ x\rightarrow +\infty }{\lim }\dfrac{(2e^{x^{2}})^{\prime }}{(3x)^{\prime }}=\underset{x\rightarrow +\infty }{\lim }\dfrac{2e^{x^{2}}\cdot 2x}{3 }=\left[ \dfrac{\infty}{3} \right] =\infty . =\underset{ x\rightarrow +\infty }{\lim }\dfrac{(2e^{x^{2}})^{\prime }}{(3x)^{\prime }}=\underset{x\rightarrow +\infty }{\lim }\dfrac{2e^{x^{2}}\cdot 2x}{3 }=\left[ \dfrac{\infty}{3} \right] =\infty .](https://port.edu.p.lodz.pl/filter/tex/pix.php/0287e8713487754bc8128c0558c0d206.png)
![\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{\ln (\sin x )}{\ln ^{2}{x}}=\left[ \dfrac{-\infty }{\infty }\right] \overset{\text{H}}{=}\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{\frac{1}{\sin x}\cdot \cos x}{2\ln x \cdot \frac{1}{x}}=\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{x}{\sin x} \cdot \dfrac{\cos x}{2\ln x}=\left[ 1\cdot\dfrac{1}{-\infty}\right] =0 \underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{\ln (\sin x )}{\ln ^{2}{x}}=\left[ \dfrac{-\infty }{\infty }\right] \overset{\text{H}}{=}\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{\frac{1}{\sin x}\cdot \cos x}{2\ln x \cdot \frac{1}{x}}=\underset{x\rightarrow 0^{+}}{\lim }\,\dfrac{x}{\sin x} \cdot \dfrac{\cos x}{2\ln x}=\left[ 1\cdot\dfrac{1}{-\infty}\right] =0](https://port.edu.p.lodz.pl/filter/tex/pix.php/d561fe251231a59d20bc3ef61fef5c00.png)
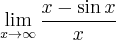
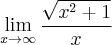
![\underset{x\rightarrow +\infty }{\lim }\, \dfrac{x-\sin x }{x} = \left[\dfrac{\infty}{\infty}\right], \underset{x\rightarrow +\infty }{\lim }\, \dfrac{x-\sin x }{x} = \left[\dfrac{\infty}{\infty}\right],](https://port.edu.p.lodz.pl/filter/tex/pix.php/1fce53623ff80629e513e56fdaaa02ee.png)
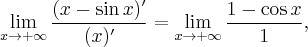
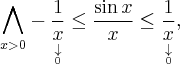
![\underset{x\rightarrow +\infty }{\lim }\dfrac{x-\sin x }{x}=\underset{x\rightarrow +\infty }{\lim }\left(1-\dfrac{\sin x}{x} \right)=[1-0]=1. \underset{x\rightarrow +\infty }{\lim }\dfrac{x-\sin x }{x}=\underset{x\rightarrow +\infty }{\lim }\left(1-\dfrac{\sin x}{x} \right)=[1-0]=1.](https://port.edu.p.lodz.pl/filter/tex/pix.php/8d0df21e7261733e76d66d0d045c8cca.png)
![\underset{x\rightarrow \infty}{\lim }\,\dfrac{\sqrt{x^2+1}}{x}=\left[\dfrac{\infty}{\infty}\right]\overset{\text{H}}{=}\underset{x\rightarrow \infty}{\lim }\,\dfrac{\frac{1}{2\sqrt{x^2+1}}\cdot 2x}{1}=\underset{x\rightarrow \infty}{\lim }\,\dfrac{x}{\sqrt{x^2+1}}\overset{\text{H}}{=}\underset{x\rightarrow \infty}{\lim }\,\dfrac{\sqrt{x^2+1}}{x}, \underset{x\rightarrow \infty}{\lim }\,\dfrac{\sqrt{x^2+1}}{x}=\left[\dfrac{\infty}{\infty}\right]\overset{\text{H}}{=}\underset{x\rightarrow \infty}{\lim }\,\dfrac{\frac{1}{2\sqrt{x^2+1}}\cdot 2x}{1}=\underset{x\rightarrow \infty}{\lim }\,\dfrac{x}{\sqrt{x^2+1}}\overset{\text{H}}{=}\underset{x\rightarrow \infty}{\lim }\,\dfrac{\sqrt{x^2+1}}{x},](https://port.edu.p.lodz.pl/filter/tex/pix.php/74c72acd6e48e1e5fecae1f74178c6ab.png)